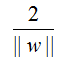【机器学习】4.支持向量机（上）

1.背景

    1.1最早是由Vladimor N.Vapnik和Alexey Ya.Chervonenkis在1963年提出。

    1.2目前的版本（soft margin）是由Corinna Cortes和Vapnik在1993年提出，并在1995年发表。

    1.3深度学习（2012）出来之前，SVM被认为是机器学习中近十几年来最成功的，表现最好的算法。

2.机器学习的一般框架：

    训练集→提取特征向量→结合一定的算法→得到结果

3.

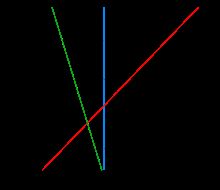
    3.1例子：

                                                                

        分两类，显然红线分类效果好。

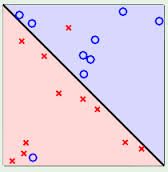
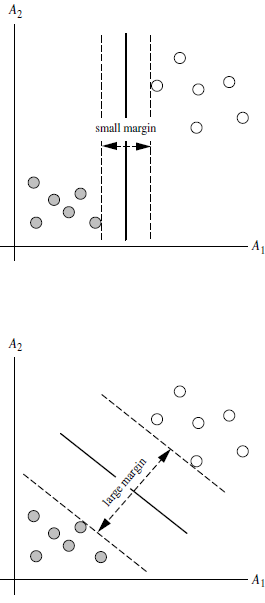
    3.2 SVM寻找区分两类的超平面（hyper plane），使边际（margin）最大。

                                                                

        总共可以有无数个可能的超平面，但我们要选取使margin最大的超平面（max margin hyperplane）

        超平面到一侧最近点的距离要等于到另一侧最近的的距离，两侧的两个超平面平行。

    3.3线性可区分和线性不可区分

                                                                        

                                                                        

                                                                   

4.定义与公式建立

    超平面可以定义为：

                                                                    

    W：weight vector

                                                                    

    n是特征值个数     X是训练实例    b：bias

    w ：一行n列    X：n行一列

                                                                

    4.1假设2维特征向量：X=（x1,x2）

    把b想成额外的weight

    超平面方程变为：

                                                            

    所有超平面右上方的点满足：

                                                              

    所有超平面左上方的点满足：

                                                               

    调整weight,使超平面定义边际的两边：

                                                        

    综合以上两式，得到：

                                                            

    所有坐落在边际的两边的超平面上的被称作“支持向量”。因为用它们来支撑我们所建立的超平面的边际，所以有这个名字。

    分界的超平面H1和H2上任意一点的距离为：

                                                                    

   ( 其中是向量的范数)

    所以两个边际间的距离为：

                                                                    

    

5.求解

    5.1 SVM找到最大边际超平面（MMH）的方法。

    利用一些数学推导，以上问题可以变为有限制的凸优化问题，利用KKT条件和拉格朗日公式，可以推出MMH可被表示为以下“决定边界”（这里不作推导）

                                                            

    其中：

    l是支持向量点个数

    Xi是支持向量点

    yi是支持向量点Xi的类别标记（+-1）

    X是要测试的实例

    b0和是卡格朗日的乘数

    5.2 对于任何测试（要归类的）实例，带人以上公式，得出的符号是正还是负决定实例的类别。

    6.例子：

    现在要求先用两个点（1,1）和（2,3）的差求出weight vector为（a,2a）,因为这两个点在超平面上，所以g(1,1)=-1,g(2,3)=1 求出a的值，然后算出weight vector,再解出w0

7.用python调用svm

    （1）例1，上图所示的例子。

# -*- coding: utf-8 -*-
from sklearn import svm

x=[[2,0],[1,1],[2,3]]           # 实例点
y=[0,0,1]                       #实例点的标签
clf=svm.SVC(kernel='linear')    #建立线性分类器，调用SVC函数
clf.fit(x,y)                    #建立模型 输出实例点和实例点标签
print clf               
print clf.support_vectors_      #֧支持向量点
print clf.support_              #支持向量点的序号
print clf.n_support_            #两个类中分别有几个支持向量
print clf.predict([2,1])        #预测给出点属于哪一类

    （2）例2

# -*- coding: utf-8 -*-
print(__doc__)
import numpy as np
import pylab as pl          #画图
from sklearn import svm

np.random.seed(0)       #随机生成一系列点，0的意思是 第一次运行程序包后以后每次运行程序生成的点都是这些点
X=np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]]    #randn(20,2)-[2,2]通过均值为2方差为2的正态分布随机产生20个数靠下方（+为靠上方），每个点都是2维 
Y=[0]*20+[1]*20     #20个点标记为0，20个点标记为1

clf=svm.SVC(kernel='linear')
clf.fit(X,Y)

#画第一条线
w=clf.coef_[0]
a=-w[0]/w[1]            #斜率
xx=np.linspace(-5,5)        #从-5到5产生连续的值
yy=a*xx-(clf.intercept_[0]/w[1])            #clf.intercept_[0}/w[1]是截距

#画第2,3条线
b=clf.support_vectors_[0]
yy_down=a*xx+(b[1]-a*b[0])
b=clf.support_vectors_[-1]
yy_up=a*xx+(b[1]-a*b[0])

print "w:",w
print "a:",a
print"support_vectors_:",clf.support_vectors_
print"clf.coef_:",clf.coef_

pl.plot(xx,yy,'k-')
pl.plot(xx,yy_down,'k--')
pl.plot(xx,yy_up,'k--')

pl.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],
           s=80,facecolors='none')
#pl.scatter(X[:,0],X[:,1],c=Y,camp=pl.cm.Paired)
pl.axis('tight')
pl.show()