乐师理工ACM集训 - 并查集与种类并查集

HDU1232 畅通工程【并查集】

传送门：HDU1232 畅通工程

解题思路

  通过并查集将已经连通的城市合并到一个集合中，最后统计有多少个集合，N个集合需要N-1条边连通起来。

AC代码

#include
using namespace std;
#define IOS ios::sync_with_stdio(false);
typedef long long ll;
typedef pair<int,int> p;
const int MAXN=1e3+5;
const int INF=0x3f3f3f3f;
int pre[MAXN];
void init()
{
	for(int i=0;i<MAXN;i++)
		pre[i]=i;
}
int _find(int x)
{
	if(x==pre[x])
		return x;
	// 路径压缩
	return pre[x]=_find(pre[x]);
}
void merge(int x,int y)
{
	x=_find(x);
	y=_find(y);
	if(x!=y)
		pre[x]=y;
}
int main()
{
	int n,m,a,b;
	while(scanf("%d",&n)&&n)
	{
		scanf("%d",&m);
		init();
		for(int i=0;i<m;i++)
		{
			scanf("%d%d",&a,&b);
			merge(a,b);
		}
		int ans=0;
		for(int i=1;i<=n;i++)
			if(pre[i]==i) // 有几个集合
				ans++;
		printf("%d\n",ans-1); // n个集合，n-1条边即可连接
	}
    return 0;
}

HDU1856 More is better【并查集+统计集合中元素个数+离散化思想】

传送门：HDU1856 More is better

题目大意

  王先生想找一些男孩帮他完成一个项目，要求找到的男孩彼此之间全是朋友（直接或者间接）。给定一个n（(0 ≤ n ≤ 100 000)）和n组朋友关系（A ≠ B, 1 ≤ A, B ≤ 10000000），问最终王先生能找到的男孩数量最多为多少？

解题思路1

  通过并查集处理朋友关系，在合并过程中更新单个集合的最大人数。
  这道题数据太水了，多组样例*O(1e7)的遍历初始化能过，并查集数组开1e5也能过，可以推测A，B的实际范围小于等于1e5。

AC代码1【未离散化水过】

#include
using namespace std;
#define IOS ios::sync_with_stdio(false);
typedef long long ll;
typedef pair<int,int> p;
const int MAXN=1e7+5;
const int INF=0x3f3f3f3f;
int pre[MAXN],cnt[MAXN],ans;
void init()
{
	for(int i=1;i<MAXN;i++)
	{
		pre[i]=i;
		cnt[i]=1;// 一个人单独一个集合
	}
}
int _find(int x)
{
	if(x==pre[x])
		return x;
	//路径压缩
	return pre[x]=_find(pre[x]);
}
void merge(int x,int y)
{
	x=_find(x);
	y=_find(y);
	if(x!=y)
	{
		pre[x]=y;
		// 集合人数累加，x指向 y,则以 y为根结点集合人数为 cnt[y]+=cnt[x]
		cnt[y]+=cnt[x]; 
		if(cnt[y]>ans)
			ans=cnt[y]; //更新集合最大人数
	}
}
int main()
{
	int n,a,b;
	while(~scanf("%d",&n))
	{
		if(n==0) // 特判，当没有朋友关系时，只能是1个人
		{
			puts("1");
			continue;
		}
		init();
		ans=1;
		for(int i=0;i<n;i++)
		{
			scanf("%d%d",&a,&b);
			merge(a,b);
		}
		printf("%d\n",ans);
	}
    return 0;
}

解题思路2

  如果严格卡数据，这道题该怎么处理呢？
  可以用离散化思想处理，已知最多10W组关系，最多也就20W个不同的数，这些数编号在[1,100W]范围内，跨度太大容易导致部分空间浪费和徒增处理时间。我们可以将编号通过离散化思想映射到[1,20W]的区间内处理。
  为什么可以这样呢？因为在这里我们只需要数据间的关系，而不关心数据的实际值。
  举个例子：

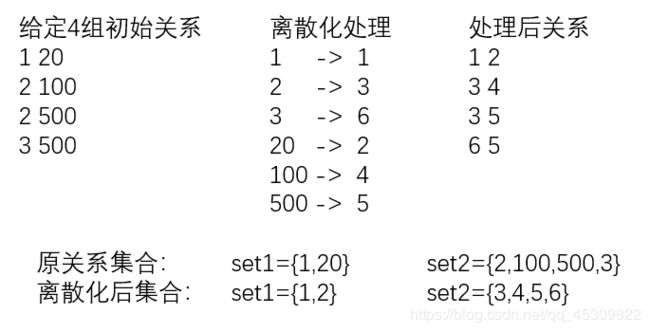
AC代码2【并查集+离散化思想】

#include
using namespace std;
#define IOS ios::sync_with_stdio(false);
#define debug printf("---\n");
#define see(x) printf("%d\n",x);
typedef long long ll;
typedef pair<int,int> p;
const int MAXN=2e5+5;
const int INF=0x3f3f3f3f;
int pre[MAXN],cnt[MAXN],ans,id;
map<int,int> mp;
void init(int n)
{
	for(int i=1;i<n;i++)
	{
		pre[i]=i;
		cnt[i]=1;// 一个人单独一个集合
	}
}
int _find(int x)
{
	if(x==pre[x])
		return x;
	//路径压缩
	return pre[x]=_find(pre[x]);
}
void merge(int x,int y)
{
	x=_find(x);
	y=_find(y);
	if(x!=y)
	{
		pre[x]=y;
		// 集合人数累加，x指向 y,则以 y为根结点集合人数为 cnt[y]+=cnt[x]
		cnt[y]+=cnt[x]; 
		if(cnt[y]>ans)
			ans=cnt[y]; //更新集合最大人数
	}
}
int main()
{
	int n,a,b;
	while(~scanf("%d",&n))
	{
		if(n==0) // 特判，当没有朋友关系时，只能是1个人
		{
			puts("1");
			continue;
		}
		init(MAXN);
		ans=1,id=1;
		for(int i=0;i<n;i++)
		{
			scanf("%d%d",&a,&b);
			if(!mp.count(a)) // 这个数没出现过，给他重新分配一个编号
				mp[a]=id++;
			if(!mp.count(b)) // 这个数没出现过，给他重新分配一个编号
				mp[b]=id++;
			merge(mp[a],mp[b]); // 对重新分配的编号建立关系
		}
		printf("%d\n",ans);
		mp.clear();
	}
    return 0;
}

对比解释：

  这里用的离散化并不是标准的离散化，标准的离散化是将无限空间中有限的个体映射到有限的空间中去且不改变相对大小，这里只是借助了离散化的思想,将数据重新进行唯一编号,并没有保持数据的相对大小，因为没有必要。
  可以看出离散化后空间复杂度明显减小，对于时间复杂度与预想不一样，我们可以根据数组开1e5也能过，推测测试数据的A,B范围在[1,1e5]（与题目实际描述不一致），那么我们的离散化处理自然是多余的，且离散化处理也会耗费一定时间。
  注意： 本题是因为测试数据太水所以不离散化也能过，如果数据足够严格呢？我们思考的时候要充分考虑到数据的上限。

计蒜客A1139 程序设计：引爆炸弹【DFS/并查集】

传送门：计蒜客A1139 程序设计：引爆炸弹

解题思路1

  将炸弹的行和列（对列做偏移处理）合并到一个集合，当所有操作结束，会形成若干个集合。每次引爆炸弹都是引爆一个集合，这样可以达到次数最少。最终集合个数即为答案。

AC代码1【并查集】

#include
using namespace std;
#define IOS ios::sync_with_stdio(false);
typedef long long ll;
typedef pair<int,int> p;
const int MAXN=1e3+5;
const int INF=0x3f3f3f3f;
int pre[MAXN<<1],vis[MAXN<<1];
char mp[MAXN][MAXN];
void init(int n)
{
	for(int i=1;i<n;i++)
		pre[i]=i;
}
int _find(int x)
{
	if(x==pre[x])
		return x;
	return pre[x]=_find(pre[x]);
}
void merge(int x,int y)
{
	x=_find(x);
	y=_find(y);
	if(x!=y)
		pre[x]=y;
}
int main()
{
	init(MAXN<<1);
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++)
		scanf("%s",mp[i]);
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<m;j++)
		{
			if(mp[i][j]=='1')
			{
				merge(i,j+n);
				vis[i]=vis[j+n]=1;
			}
		}
	}
	int ans=0;
	for(int i=0;i<n+m;i++)
		if(vis[i] && _find(i)==i) // 有炸弹且是独立集合
			ans++;	
	printf("%d\n",ans);
    return 0;
}

解题思路2

  碰到一个炸弹就引爆，将其变为’0’表示该位置的炸弹已经被引爆了，然后把该炸弹的行和列标记（表示已经处理过了，后续不需要重复处理），继续引爆该行和列的其他炸弹，一直引爆下去，直到不能引爆。（dfs的过程就是一个连锁反应的过程）
  首次引爆次数（即不算连锁引爆的）即为答案。

AC代码2【DFS】

#include
const int MAXN=1e3+5;
char g[MAXN][MAXN]; //存图
int r[MAXN],c[MAXN]; //标记行、列
int ans=0;
int n,m;
void dfs(int x,int y)
{
	g[x][y]='0'; // 置为'0'表示该位置的炸弹已经被引爆了
	if(!r[x]) // 该行未被处理过
	{
		r[x]=1;
		for(int i=0;i<m;i++) // 对该行的炸弹继续进行连锁引爆
			if(g[x][i]=='1')
				dfs(x,i);
	}
	if(!c[y]) // 该列未被处理过
	{
		c[y]=1;
		for(int i=0;i<n;i++) // 对该列的炸弹继续进行连锁引爆
			if(g[i][y]=='1')
				dfs(i,y);
	}	
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++)
		scanf("%s",&g[i]);
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<m;j++)
		{
			if(g[i][j]=='1') // 引爆并进行连锁反应
			{
				dfs(i,j);
				ans++;
			}
		}
	}
	printf("%d\n",ans);
	return 0;
}

HDU1829 A Bug’s Life【种类并查集】

传送门：HDU1829 A Bug’s Life

题目大意

  给定T组测试样例，每组样例给定一个虫子数量n（1<=n<=2000）和关系数量m(m<=1000000)，接下来是m组关系，每组关系表示两个虫子是异性（性别只有两种）。问是否有自相矛盾的情况?

比如给定3组异性关系
1 2
2 3
1 3
(1,2)是异性，(2,3)是异性，
按理来说(1,3)应该是同性，
题中却给出(1,3)也是异性，此时就自相矛盾了。

解题思路

  种类并查集

AC代码

#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define IOS ios::sync_with_stdio(false);
typedef long long ll;
typedef pair<int,int> p;
const int MAXN=2005;;
const int INF=0x3f3f3f3f;
int pre[MAXN*2];
void init(int n)
{
	for(int i=0;i<n;i++)
		pre[i]=i;
}
int _find(int x)
{
	if(x==pre[x])
		return x;
	return pre[x]=_find(pre[x]);
}
void merge(int x,int y)
{
	x=_find(x);
	y=_find(y);
	if(x!=y)
		pre[x]=y;
}
int main()
{
	int T,n,m,a,b,flag;;
	scanf("%d",&T);
	for(int i=1;i<=T;++i)
	{
		init(MAXN<<1);
		flag=0;
		scanf("%d%d",&n,&m);
		while(m--)
		{
			scanf("%d%d",&a,&b); // 给定一组异性关系
			if(_find(a) == _find(b)) // 根据前面的推导发现应该是同性
				flag=1; // 自相矛盾
			else // 建立异性关系
			{
				merge(a,b+n); 
				merge(b,a+n);
			}
		}
		if(flag)
			printf("Scenario #%d:\nSuspicious bugs found!\n",i);
		else
			printf("Scenario #%d:\nNo suspicious bugs found!\n",i);
		if(i<T)
			printf("\n");	
	}
    return 0;
}

POJ1182 食物链【种类并查集】

传送门：POJ1182 食物链

解题思路

  种类并查集经典题型

AC代码

#include
#include
#include
#include
#include
#include
using namespace std;
#define IOS ios::sync_with_stdio(false);
typedef long long ll;
typedef pair<int,int> p;
const int MAXN=50005;;
const int INF=0x3f3f3f3f;
int pre[MAXN*3];
void init(int n)
{
	for(int i=0;i<n;i++)
		pre[i]=i;
}
int _find(int x)
{
	int son=x,temp;
	// 找根结点
	while(pre[x]!=x)
		x=pre[x];
	// 将沿途结点全部指向根结点
	while(son!=x)
	{
		temp=pre[son];
		pre[son]=x;
		son=temp;	
	}
	return x;
}
void merge(int x,int y)
{
	x=_find(x);
	y=_find(y);
	if(x!=y)
		pre[x]=y;
}
int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
    init(3*n);
	int ans=0;
    while(m--)
	{
        int op,a,b;
		scanf("%d%d%d",&op,&a,&b);
		if(a<1 || a>n || b<1 || b>n) // 不在范围内
		{
			ans++;
			continue;
		}
		if(op==2 && a==b) // 自己吃自己
		{
			ans++;
			continue;
		}
		if(op==1) // x,y是同类
		{
			if(_find(a)==_find(b+n)||_find(b)==_find(a+n)) // 根据前面的话发现是捕食关系
				ans++;
			else // 建立同类关系
			{
				merge(a,b);
				merge(a+n,b+n);
				merge(a+2*n,b+2*n);
			}
		}
		else // x捕食y
		{
			if(_find(a)==_find(b)||_find(b)==_find(a+n)) // 发现是同类或者是 y捕食x
				ans++;
			else // 建立捕食关系
			{
				merge(a,b+n);
				merge(a+n,b+2*n);
				merge(a+2*n,b);			
			}
		}
    }
    printf("%d\n",ans);
    return 0;
}