支持向量机

支持向量机（SVM）一

---

在看这篇文章之间，建议先看一下感知机，这样可以更好的看懂SVM。

---

---

一、最大间隔分类器

在之前的文章感知机中提到过，感知机模型对应于特征空间中将实例划分为正负两类的分离超平面，但是，感知机的解却不止一个。对同一个数据集而言，可以计算得到很多的感知机模型，不同的感知机的 训练误差 都是一样的，都为0。

那么，这些训练误差都为0的感知机模型中，如何针对当前数据集，选择一个最好的感知机模型呢？现在就需要考虑模型的 泛化误差 了。即，在所有训练误差为0的感知机中，选择泛化误差最小的那个感知机，这就是SVM算法最初的目的。

基本的SVM（最大间隔分类器）是一种二分类模型，它是定义在特征空间上的间隔最大的线性分类器，间隔最大是SVM和感知机不同的地方，间隔最大化对应于泛化误差最小。

---

1.1 决策面

面对一个线性可分的二分类问题，将正负样本分开的超平面，称为决策面。

和 线性回归 模型一样，这里一般会使用一些特征函数 ϕ(x) ，将输入空间映射到新的特征空间中，再进行计算。

y(x)=f(wTϕ(x)+b)

这里 f(⋅) 叫做激活函数， w 是线性模型的系数， b 一般被叫做偏置：

f(a)={+1−1a≥0a<0

这里输出的取值为 t∈{+1,−1} ，即正负样本。这里的 {+1,−1} 仅仅是一个标号，代表正负样本，并不是具体的数值。如果感觉不喜欢 {+1,−1} ，可以和Logistics Regression一样，使用 {0,1} 也行。而且，可以使用 {+1,−1} 主要也是因为这里是二分类问题，遇到多分类问题的时候，还得考虑其他的标号方式。

如果感觉 ϕ(x) 这种表述方式不太习惯，可以考虑所有的 ϕ(x)=x ，这样就和一般的书上的公式一致了。这种表达仅仅是我个人的喜好，式主要是为了强调，在实际问题中，输入空间 x 一般不会作为模型的输入，而是要将输入空间通过一定的特征转换算法 ϕ(x) ，转换到特征空间，最后在特征空间中做算法学习。而且，在实际问题中，各种算法基本上都是死的，但是，特征变换的这个过程 ϕ(x) 却是活的，很多时候，决定一个实际问题能不能很好的解决， ϕ(x) 起着决定性的作用。举个简单的例子，比如Logistics Regression，数据最好要做归一化，如果数据不归一化，那么那些方差特别大的特征就会成为主特征，影响模型的计算， ϕ(x) 就可以做这个事情。再或者后面要降到的核函数问题，核函数SVM能解决非线性可分问题，主要也是基于使用 ϕ(x) 来做非线性特征变换。

作为一个决策面：
当样本的标号 tn=+1 的时候，该样本为正样本。如果样本被正确分类，那么 wTϕ(xn)+b>0 ， f(wTϕ(x)+b)=+1
当样本的标号 tn=−1 的时候，该样本为负样本。如果样本被正确分类，那么 wTϕ(xn)+b<0 ， f(wTϕ(x)+b)=−1

**究竟什么是决策面？
答:决策面就是能够将正负样本分开的点的集合，比如上面的模型中，决策面的数学表达式为： wTϕ(x)+b=0 ，决策面就是这个式子的解集，所以，一般我们就直接用这个式子代表决策面了。可以看到，对于这个决策面的数学表达式而言， w 和 b 的数值并不重要。比如， wTϕ(x)+b=0 和 2wTϕ(x)+2b=0 ，后一个决策面的参数数值是前一个决策面数值的两倍，但这两个决策面的解是一样的，也就是说其得到的点集是一样的，那么这两个表达式所表示的就是同一个决策面。所以，这里我要强调一点，对于一个线性决策面而言，重要的不是 w 和 b 的取值，重要的是 w 和 b 的比值， w 和 b 的比值决定了一个决策面的点集，也就决定了一个决策面。**

---

1.2 最优决策面

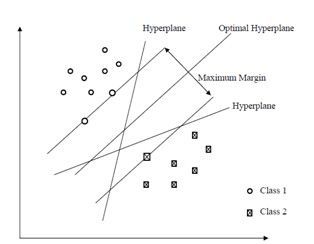
对于线性可分的二分类问题而言，使用 感知机 算法，可以得到很多很多满足上述要求的决策面，比如下图中，就是可以将正负两类数据分开的两个决策面。

那么，在这些决策面中，哪个决策面，才是最优的决策面呢？首先，需要明确，上述的决策面，都是可以将训练样本正确分类的决策面，也就是说，上述决策面的 训练误差 都为0。要从这些训练误差都为0的模型中，选出一个最好的模型，很自然的，就需要考虑模型的 泛化误差 。

最大间隔分类器认为，决策面的泛化误差可以用训练样本集合中，离决策面最近的样本点到决策面的间隔（margin）来表示，离决策面最近的样本点，到决策面的间隔（margin）越大，那么，这个决策面的泛化误差就越小。直观的来讲，最优决策面差不多就是下面这幅图中，中间的那个决策面。

---

1.3 最小间隔

什么是间隔？
答：首先，要搞清楚是谁和谁的间隔，在这里指的是一个 训练样本点 和 决策面 之间的间隔。

那么，间隔又如何定义的呢？
答：间隔，就是样本点到决策面之间的距离，由中学的知识就可以知道，一个样本点 xn 到一个面 wTϕ(x)+b=0 ，的距离为（这里可以直接认为是点到直线的距离）：

rn=wTϕ(xn)+b||w||

但这个距离在数值上会存在正负的问题，由于样本点类别取值 tn∈{+1,−1} ，所以样本点到决策面的间隔可以改为：

rn=tn{wTϕ(xn)+b}||w||

当 tn=+1 的时候，如果样本被正确分类， wTϕ(xn)+b>0 ，上述样本点到决策面的间隔 rn 取正值
当 tn=−1 的时候，如果样本被正确分类， wTϕ(xn)+b<0 ，上述样本点到决策面的间隔 rn 仍然取正值
这样，分类正确的样本点的间隔就永远是正的了。

显然，一旦决策面有了，那么训练集合中的每个样本点 xn 到决策面都会有一间隔 rn 。自此，就可以定义样本集合到决策面最小的间隔 r 为：

r=minntn{wTϕ(xn)+b}||w||;n∈{1,2,...,N}

既然 r 是最小间隔，毫无疑问，对于任意一个样本点 xn 而言：

tn{wTϕ(xn)+b}||w||≥r

---

1.4 最小间隔最大化

前面已经说了，要使用决策面在训练样本中的最小间隔 r 来表示决策面的训练误差：最小间隔 r 越大，那么其泛化误差就越小，模型就越好。而我们这里，就是在所有可选的决策中，找出其对应的最小间隔 r 最大的那个决策面，而决策面是用参数 w 和 b 定义的，所以，最小间隔最大化可以形式化为：

argmaxw,b{minntn{wTϕ(xn)+b}||w||}

用优化理论的形式重写一下上面的式子，可以得到：

maxw,brst：ti{wTϕ(xi)+b}||w||≥r   ;i=1,2,...N

将上面的约束条件变一下型可得：

maxw,brst：ti{wTϕ(xi)+b}≥r||w||   ;i=1,2,...N

在前面已经提到过，对于一个决策面 wTϕ(xi)+b=0 而言， 重要的不是 w 和 b 的取值， wTϕ(x)+b=0 和 2wTϕ(x)+2b=0 的所得到的 x 的点集是一样的，即其决策面是一样的，这里真正重要的是 w 和 b 的比值。

w 和 b 的比值，决定了一个决策面的点集，也就决定了一个决策面。

所以，只要有一个决策面，那么，唯一确定的是 w 和 b 的比值，但是， w 和 b 具体的取值是可以改变的，只要 w 和 b 按比例改变，决策面就是确定不变的。

也就是说， w 和 b 的比值比值不变的情况下， w 是可以任意取值的。这样的话，为了便于计算，我们就取：

||w||=1r

那么，上面的式子又可以改写为：

maxw,b1||w||st：ti{wTϕ(xi)+b}≥1;i=1,2,...N

可以看到，上面的式子最大化的目标函数变成了 1/||w|| ，很容易知道，其等价于 最小化 ||w||2 ，那么最小间隔最大化，最终就可以变为下面这个最小化的约束优化问题：

minw,b||w||2st：ti{wTϕ(xi)+b}≥1;i=1,2,...N

这里，最小间隔为：

r=1||w||

在网上博客还有现有的书籍中，对于最小间隔最大化的解释，都使用了函数间隔和几何间隔的概念，我个人在第一次接触这两个概念的时候，就有些被弄糊涂了，理解了这两个概念之后，又感觉这种解释过于冗余、牵强，完全是为了解释最小间隔最大化而解释最小间隔最大化。所以，这里我直接抛弃函数间隔和几何间隔的概念，给出我个人的一种解释。

最小间隔最大化后得到的决策面，就是我们要找的泛化误差最小的决策面。对于下图中两特征的二分类问题而言，可以看出， 最小间隔为 1/||w|| ，即，正样本到决策面的最小间隔为 1/||w|| ；同时，负样本到决策面的最小间隔也为 1/||w|| 。所以正负样本之间的最小间隔为 2/||w|| 。

由于间隔最小的样本点 xn 满足：

tn{wTϕ(xn)+b}||w||=r=1||w||

所以，间隔最小的正样本点 xn 满足：

wTϕ(xn)+b=1

间隔最小的负样本点 xn 满足：

wTϕ(xn)+b=−1

这里定义，拥有最小间隔的正负样本点为支持向量（support vector），也就是上图中 wTϕ(xn)+b=1 和 wTϕ(xn)+b=−1 所对应的那三个样本点。

关于支持向量机的名字，这里可以稍微说一下，因为这个名字并不是特别的好理解。首先是支持（support），根据柯林斯词典，support的主要意思：the activity of providing for or maintaining by supplying with money or necessities，表示的是提供一些必须品的意思。vector指的就是样本点，这个问题不大。那么问题来了，为什么将间隔最小的那些样本点叫做support vector（或者可以直接说是support point）呢？答：从图中可以看出，对于决策面而言，要想唯一的确定这个决策面，就是要根据最小的间隔 r 来得到，也就是说，决策面仅仅和拥有最小间隔的那些样本点相关，和其他那些间隔大于最小间隔的样本点，是没有关系的。即：拥有最小间隔的那些样本点是决策面所必须的，而间隔大于最小间隔的样本点的有无，对决策面并不构成影响。所以将拥有最小间隔的那些样本点叫做support point， 也就是support vector。

---

1.5 拉格朗日对偶性

在求解约束最优化问题的过程中，我们常常会使用拉格朗日对偶性（Lagrange duality），把原始问题（primal problem）转换为对偶问题（dual problem）来求解，基于对偶问题的求解来得到原始问题的解。这个方法在统计学中经常使用，不仅仅本文的SVM算法用到了拉格朗日对偶性，后面要讲的最大熵模型也用到了拉格朗日对偶性。这里仅仅对拉格朗日对偶性做一个简述，我个人认为，主要知道其概念和结果即可，无需深究。拉格朗日对偶性的详细说明，可以参见Boyd的《Convex Optimization》，该书用一整个章节的篇幅来详细的论述了拉格朗日对偶性的问题。

对于一个线性规划问题，我们称之为原始问题，都有一个与之对应的线性规划问题我们称之为对偶问题。原始问题与对偶问题的解是对应的，得出一个问题的解，另一个问题的解也就得到了。并且原始问题与对偶问题在形式上存在很简单的对应关系：
- 目标函数对原始问题是极大化，对偶问题则是极小化
- 原始问题目标函数中的系数，是对偶问题约束不等式中的右端常数，而原始问题约束不等式中的右端常数，则是对偶问题中目标函数的系数
- 原始问题和对偶问题的约束不等式的符号方向相反
- 原始问题约束不等式系数矩阵转置后，即为对偶问题的约束不等式的系数矩阵
- 原始问题的约束方程数对应于对偶问题的变量数，而原始问题的变量数对应于对偶问题的约束方程数
- 对偶问题的对偶问题是原始问题

1、原始问题

假设，有 f(x),ci(x),hj(x) ，他们是定义在空间 Rn 上的连续可微的函数，也就是可导函数的意思。其约束最优化问题为：

minx∈Rnf(x)s.t.  ci(x)hj(x)≤0;i=1,2,...,k=0;j=1,2,...,l

这里 ci(x) 是不等式优化，而 hj(x) 是等式优化。

上面这种约束优化问题的形式成为原始问题。

现在，引入拉格朗日函数：

L(x,α,β)=f(x)+∑i=1kαici(x)不等式约束+∑j=1lβjhj(x)等式约束

这里 αi 和 βj 是拉格朗日乘子，且， αi≥0 。也就是说，不等式约束 ci(x) 的拉格朗日乘子要大于等于0，而等式约束 hj(x) 的拉格朗日乘子并没有限制。

现在考虑最大化这个拉格朗日函数，定义：

θp(x)=maxα,β;αi≥0L(x,α,β)=maxα,β;αi≥0{f(x)+∑i=1kαici(x)+∑j=1lβjhj(x)}

对于上面的最大化式子有：

• 如果不等式约束 ci(x)<0 ，等式约束 hj(x)=0 ，那么上式最大化就会使得 αi=0 ， βj 可以取任意值。 此时所有满足约束条件的，并且最大化结果为 θp(x)=f(x) 。
• 如果不等式约束 ci(x)=0 ，等式约束 hj(x)=0 ，那么上式最大化就会使得 αi>0 , βj 可以取任意值。此时是满足约束条件的，并且最大化结果为 θp(x)=f(x) 。
• 如果存在不等式约束 ci(x)>0 , 等式约束 hj(x)=0 ，即此时存在不等式约束违反约束条件，那么要使得上式最大化，必然会使得 αi=∞ ，进而使得 θp(x)=∞ 。
• 如果不等式约束 ci(x)≤0 , 存在 hj(x)≠0 ，那么要使得上式最大化，必然会使得 βj=∞ ，进而使得 θp(x)=∞ 。

综上所述，可以知道：

θp(x)=maxα,β;αi≥0L(x,α,β)={f(x)∞ci(x)≤0 和 hj(x)=0 都满足时当存在违反ci(x)≤0 或者hj(x)=0 条件时

由于原始最优化问题就是要在满足约束条件下，求解最小化的 f(x) 。而由上可知，在满足约束条件的情况下， f(x)=θp(x)=maxα,β;αi≥0L(x,α,β) 。

也就是说，原始约束最优化问题：

minx∈Rnf(x)s.t.  ci(x)hj(x)≤0;i=1,2,...,k=0;j=1,2,...,l

中的 f(x)，ci(x)≤0，hj(x)=0 就可以用 θp(x)=maxα,β;αi≥0L(x,α,β) 来代替。

于是乎，原始约束最优化问题就变成了一个极小极大化的问题：

minxθp(x)=minxmaxα,β;αi≥0L(x,α,β)

很显然，这个极小极大化问题，和原始问题是等价的。

为了方便，这里定义原始问题（primal problem）的最优解为：

p∗=minxθp(x)

2、对偶问题

对于一块磁铁而言，磁铁有N极和S极，N极和S极只是同一块磁铁的不同表现而已，这两个极性虽然不同，但是却拥有相同的本质：磁。他们是相辅相成的，是同一个事物的两种不同表现。就像有阴必有阳；有光明必有黑暗；而阴阳本为一体，明暗实为一物，他们都是同一个东西的不同表现而已，这个是世间万物的规律。

对偶问题和原始问题也是一样，他们是优化问题的两个不同表现形式而已，他们本质上是一个东西，只是表现的方式相反罢了。

考虑原始问题：

θp(x)=maxα,β;αi≥0L(x,α,β)

原始问题是以 α,β 为参数，以 x 为变量的极大化问题。既然对偶问题是原始问题关于优化问题的相反的表达方式，那么对偶问题就可以写成，以 α,β 为变量，以 x 为参数的极小化问题(记住一点：本质相同，表现相反):

θD(α,β)=minxL(x,α,β)

原始问题最终是被极小化，成为了一个极小极大化的问题：

minxθp(x)=minxmaxα,β;αi≥0L(x,α,β)

对偶问题，要和其相反，就需要被极大化，而称为一个极大极小化的问题：

maxα,β;αi≥0θD(α,β)=maxα,β;αi≥0minxL(x,α,β)

上面的式子，就称为拉个朗日函数的极大极小问题，并定义对偶问题（dual problem）的最优解为：

d∗=maxα,β;αi≥0θD(α,β)

由于：

θD(α,β)=minxL(x,α,β)≤L(x,α,β)≤maxα,β;αi≥0L(x,α,β)≤θp(x)

所以：

θD(α,β)≤θp(x)

上面这是式子说明， θD(α,β) 的所有的解，都不大于 θp(x） 的解。那么，毫无疑问，对偶问题的最优解和原始问题的最优解也满足这个式子：

d∗=maxα,β;αi≥0θD(α,β)≤minxθp(x)=p∗

在我们常见的问题中，只要满足一定的条件，就可以使得 d∗=p∗=L(x∗,α∗,β∗) ，这里 x∗,α∗,β∗ 就是最优解。这里所说的一定的条件，指的就是KKT条件。

3、KKT条件

对于原始问题 和 对偶问题而言， x∗,α∗,β∗ 分别是原始问题和对偶问题的解的充分必要条件是 x∗,α∗,β∗ 满足KKT条件：

∇xL(x∗,α∗,β∗)∇αL(x∗,α∗,β∗)∇βL(x∗,α∗,β∗)α∗ici(x∗)ci(x∗)α∗ihj(x∗)=0=0=0=0;i=1,2...k≤0;i=1,2...k≥0;i=1,2...k=0;j=1,2,...l

上述的KKT条件，看起来很吓人，其实很容易理解：函数 L(x,α,β) 是以 x,α,β 为参数的，那么其最优解 x∗,α∗,β∗ 定然满足 函数 L(x,α,β) 的梯度为0，这就是KKT条件的前三个等式：

∇xL(x∗,α∗,β∗)∇αL(x∗,α∗,β∗)∇βL(x∗,α∗,β∗)=0=0=0

前面已经说明过，函数 L(x,α,β) 要能够使用，最初的优化问题必须满足不等式约束 ci(x)≤0 以及其相关的拉格朗日乘子 αi 的约束：

α∗ici(x∗)ci(x∗)α∗i=0;i=1,2...k≤0;i=1,2...k≥0;i=1,2...k

而最后一个KKT条件，对应的就是 L(x,α,β) 的等式约束:

hj(x∗)=0;j=1,2,...l

---

1.6 最小间隔最大化求解

求解最小间隔最大化，就是要求解式子：

minw,b12||w||2s.t.  ti{wTϕ(xi)+b}≥1;i=1,2,...N

而求解上面的式子，用的到方法，就是拉格朗日对偶性。这里，在原来的最小化的目标函数前面加了 1/2 ,并不会影响最后的最优解，但是对后面的公式推导相对有利，故而加上了个 1/2 。

将它作为原始的优化问题，应用拉格朗日对偶性，通过求解对偶问题（dual problem）来得到原始问题（primal problem）的最优解，这个最优解，就对应于最优的决策面。

这样做的优点主要有两个：
一、对偶问题相对来说比较容易求解
二、可以很自然的引入核函数，进而推广到非线性分类器中

首先，构建拉格朗日函数，由于上面的约束优化问题中只有不等式约束，所以为所有的不等式约束添加拉格朗日乘子： αi≥0;i=1,2,...N ，则拉格朗日函数为：

L(w,b,α)=12||w||2优化目标−∑i=1Nαi(ti{wTϕ(xi)+b}−1)不等式约束

根据前面关于拉格朗日对偶性的说明可以很容易知道，这个原始问题为极小极大问题：

minw,bmaxα;αi≥0L(w,b,α)

其对应的对偶问题为极大极小问题：

maxα;αi≥0minw,bL(w,b,α)

求解内部极小化

这里首先求解内部的极小化问题：

minw,bL(w,b,α)

显然，这个极小化问题是以 w,b 为参数的，那么，先使 L(w,b,α) 对 w,b 求导，并令其为0：

∇wL(x,α,β)∇bL(x,α,β)=w−∑i=1Nαitiϕ(xi)=0=∑i=1Nαiti=0

那么，就有：

w=∑i=1Nαitiϕ(xi)∑i=1Nαiti=0

将 w=∑Ni=1αitiϕ(xi) 带入到 L(w,b,α) 中，就可以得到：

L=12||w||2−∑i=1Nαi(ti{wTϕ(xi)+b}−1)=12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}−∑i=1Nαi(ti{{∑j=1Nαjtjϕ(xj)}ϕ(xi)+b}−1)=−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+b∑i=1Nαiti+∑i=iNαi=−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi

上面推导的导数第二步使用了： ∑Ni=1αiti=0 ，最终可以得到：

minw,bL(w,b,α)=−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi

这里的 <ϕ(xi),ϕ(xj)> 是 ϕ(xi) 和 ϕ(xj) 的內积。

求解外部极大化

前面已经将内部的极小化求解得到了 minw,bL(w,b,α) ，这里再在其求解的结果上加上外层的极大化，那么就有下面这个约束优化问题：

maxα{−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi}

s.t.  ∑i=1Nαitiαi=0≥0;i=1,2,...N

这个就是原问题的对偶问题，当然了，可以将这个对偶问题的目标函数的符号换一下，让它成为一个最小化的问题:

minα{12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}−∑i=iNαi}

s.t.  ∑i=1Nαitiαi=0≥0;i=1,2,...N

公式推导到这个地方，就可以知道，上面这个最小化问题，就是我们最终要求解的问题，其最小化的目标函数是以 α 为参数的。

也就是说，假设最优解是 α∗=（α∗1,α∗2,...α∗N） 。这里暂时不讨论如何求得这个最优解，其具体的求解算法会在后面详细的论述，现在假设，我们可以通过某种算法，将上面的这个最小化的优化问题的最优解求出来。

那么，在已知这个最优解的情况下，我们来看一下，基于这个最优解，SVM的决策面是什么样的？

根据原始问题 L(w,b,α) 的KKT条件可以知道：

∇wL(x∗,α∗,β∗)∇bL(x∗,α∗,β∗)α∗i(ti{w∗Tϕ(xi)+b∗}−1)ti{w∗Tϕ(xi)+b∗}−1α∗i=w∗−∑i=1Nα∗itiϕ(xi)=0=∑i=1Nα∗iti=0=0;i=1,2,...N≥0;i=1,2,...N≥0;i=1,2,...N

那么，就有：

w∗=∑i=1Nα∗itiϕ(xi)

这里，根据已经求得的 α∗i ,就可以将 w∗ 求出来了。决策面的参数有两个: w,b ， w 求出来了，剩下的就是 b 了。

在前面讨论过，SVM是间隔最大化的决策面，支持向量对应的就是间隔最小的那些点，由前面关于间隔最大化的讨论可以知道，支持向量满足下面这个公式：

ti{wTϕ(xi)+b}−1=0

而根据前面对原始问题的讨论，可以知道，满足这个公式的点 xi （支持向量） ,在拉格朗日函数中，所对应的 α∗i>0 。所以，我们只需要找到一个 α∗i>0 , 就可以得到 b∗ :

b∗=1ti−w∗Tϕ(xi)

同时，需要注意： t2i=1 ，并带入 w∗T ，就可以将上面这个式子重写为：

b∗=ti−∑j=1Nα∗jtj<ϕ(xj),ϕ(xi)>

当然，为了稳妥起见，很多时候，我们会将所有的支持向量 xi∈S 对应的 b∗i 都求出来，然后用其均值，作为最终的 b∗ 。这里 S 是支持向量的集合，也就是 α∗i>0 所对应的点集:

b∗=1Ns∑i=1Nsb∗i

这样，就可以求得最终的决策超平面为：

∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗=0

分类决策函数可以写为：

f(x)=sign{∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗}

这里就可以发现:

• 在预测的时候， w∗ 和 b∗ 仅仅依赖于训练集合中 α∗i>0 的那些样本点，而其他样本点对 w∗ 和 b∗ 没有影响。但是，为了求得 w∗ 和 b∗ ，在训练阶段，还是需要整个样本集合。也就是说，在做预测的时候，支持向量机需要的内存空间是非常小的，只需要存储支持向量即可，预测过程和非支持向量无关。
• 分类决策函数仅仅依赖于输入 x 和 训练样本之间的內积。这个內积是后面核函数的雏形，也是SVM得以广泛应用的关键。

---

1.7 SVM、LDA、Logistics Regression 算法比较

在之前的文章线性判别分析（Linear Discriminant Analysis）中就说过：凡是分类算法，必定有决策面，而这些分类算法所不同的是:决策面是线性的还是非线性的；以及如果得到这个决策面。

对于Logistics Regression

对于一个二分类问题，在Logistics Regression中，假设后验概率为Logistics 分布：

P(C1|x)=11+exp(wTx)P(C2|x)==exp(wTx)1+exp(wTx)

这里，使用一个单调的变换函数，logit 函数： log[p/(1−p)] ，那么就可以得到：

logP(C1|x)P(C2|x)=wTx

所以Logistics Regression的决策面就是：

wTx=0

对于Linear Discriminant Analysis

这里假设 fk(x) 是类别 Ck 的类条件概率密度函数， πk 是类别 Ck 的先验概率，毫无疑问有 ∑kπk=1 。根据贝叶斯理论有：

P(Ck|x)=fk(x)πk∑Kl=1fl(x)πl

LDA假设 fk(x) 是均值不同，方差相同的高斯分布，所以其类条件概率密度函数可以写为：

fk(x)=1(2π)p/2|Σ|1/2exp(−12(x−μk)TΣ−1(x−μk))

这里，特征 x 的维度为 p 维，类别 Ck 的均值为 μk ，所有类别的方差为 Σ 。

LDA和前面提到的Logistics Regression采用的单调变换函数一样，都是logit 函数： log[p/(1−p)] ，对于二分类问题有：

logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2

所以LDA的决策面就是：

xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2