约束最优化方法之最优性条件

前面几篇博客主要讲了无约束最优化问题的一些求解方法。从这一篇博客开始将开始讲有约束的最优化方法。首先说明一下有约束最优化问题的一般形式

mins.t.f(x)s(x)≥0h(x)=0⎫⎭⎬⎪⎪(1)

。其中， f:Rn→R1，s:Rn→Rm，h:Rn→Rl 。这个问题的意思是，在容许集 D={x|s(x)≥0，h(x)=0，x∈Rn} 中寻找一点 x∗ ，是的对于任意 x∈D ，都有

f(x∗)≤f(x)

从而 x∗ 就是公式(1)的极小点。

在上面介绍了有约束最优化问题的一般形式后，其实我们可以进一步将其分解为等式约束最优化问题、不等式约束最优化问题和一般最优化问题。其中一般最优化问题的如公式(1)所示。等式约束最优化问题的一般形式为 mins.t.f(x)h(x)=0}(2) 其中 f:Rn→R1，h:Rn→Rl 。即等式约束最优化问题中的约束只有等式。
不等式约束最优化问题的一般形式为

mins.t.f(x)s(x)≥0}(3)

其中 f:Rn→R1，s:Rn→Rm ，即不等式约束最优化问题的中的约束只有不等式。
下面讲等式约束最优化条件以及不等式约束最优化条件。

等式约束最优化条件

等式约束最优化条件的一般形式如公式(2)所示，我们将等式约束的最优化问题中的等式约束拆分为

hj(x)=0j=1,2,...,l

其中 hi:Rn→R1 。这一问题的求解已经在微积分中通过Lagrange乘子法在理论上得到解决。

定理1：(Lagrange定理重述) 假设
(i) x∗ 是约束问题(2)的局部最优解
(ii) f，h1，h2，...，hl:Rn→R1 在 x∗ 的某一个邻域内连续可微
(iii) ∇h1(x∗)，∇h2(x∗)，...，∇hl(x∗) 线性无关

那么，存在实数 λ∗1，λ∗2，...，λ∗l 使得

∇f(x∗)−∑j=1lλ∗j∇hj(x∗)=0(4)

公式(4)是等式约束问题(2)的最优性一阶必要条件。

首先我们应该知道的是，对于约束最优化问题的局部极小点 x∗ ，不一定有 ∇f(x∗)=0 ，即 ∇f(x∗)=0 不再是约束最优化问题的必要条件。而定理1所指出的是，在局部最优点 x∗ 处的导数 ∇f(x∗) 与所有的约束曲面 hj(x)=0 的交集正交，因为按照定理1，我们知道 ∇f(x∗)=∑j=1l∇hj(x∗) ，即 ∇f(x∗) 在由约束曲面的法向量所张成的空间中。

通过这个定理，我们能够将等式约束问题转换为无约束问题，定义一个 n+l 元函数

L(x,λ1,λ2,...,λl)=f(x)+∑j+1lλjhj(x)(5)

我们将公式(5)称为 Lagrange函数，其中 λ1,λ2,...,λl 称为 Lagrange乘子。

Lagrange函数的梯度

∇L=[∇xL∇λL]

其中

∇xL=∇f(x)−∑j=1lλj∇xhj(x)

∇λL=[−h1(x),−h2(x),...,−hl(x)]T

由此我们知道

min L(x,λ1,λ2,...,λl)(6)

的必要条件是

∇L(x∗,λ1,λ2,...,λl)=0

这恰好给出了等式约束问题(2)的最优性条件以及等式约束。

下面给出等式约束最优化问题的充分条件。

定理2： 在等式约束问题(2)中，假设：
(i) f,h1,h2,...,hl:Rn→R1 是二次连续可微函数
(ii)存在 x∗∈Rn 与 λ∗∈Rl ，使得Lagrange函数的梯度为0，即

∇L(x,λ∗1,λ∗2,...,λ∗l)=0

(iii)对于满足条件

vT∇hj(x∗)=0j=1,2,...,l

的任意非零向量 v∈Rn ，都有

vT∇2kL(x∗,λ∗)v>0

那么， x∗ 是等式约束最优化问题(2)的严格局部极小点。

定理2的几何意义是在Lagrange函数的驻点 [x∗λ∗]T 处，如果Lagrange函数关于 x 的Hesse矩阵在 l 个约束超平面的切平面的交集上正定，那么 x∗ 就是严格局部极小点。

不等式约束最优化条件

对于不等式约束的一般形式(3)我们换一种方法表示。首先我们用 D 表示容许集，

D={x|si(x)≥0,i=1,2,...,m}

那么不等式约束的一般形式(3)又可以写为

mins.t.f(x)x∈D}(7)

定义1：对于不等式约束最优化问题(3)。设 x~∈D ,若 x~ 是的某个不等式的约束 si(x~)=0 ，则该不等式约束 si(x)≥0 称为是关于容许点 x~ 的 起作用约束；否则，若 si(x)>0 ，则该不等式约束称为是关于容许点 x~ 的 不起作用约束。

通过定义1我们能够清楚的知道，只有容许集边界上的点才能使得某一个或这某些约束条件起作用。对于上图，我们可以看出，点 AB 都是容许点，所有的约束对于容许点B来说都是不起作用约束， s2(x) 对于容许点A是起作用约束。

几何最优性条件

定义2： 设 C 是 Rn 中的非空集，且 x∈C 。对于 ∀p∈Rn ，若当 x+p∈C 时，对于 ∀t≥0 ，必有 x+tp∈C ，则集合 C 称为以 x 为定点的锥，若锥 C 为凸集，正称为凸锥。
由向量 v1,v2,...,vm 的所有非负组合构成的集合

C={x|x=∑i=1mγivi,γi≥0}

是一个以原点为定点的凸锥，由于这样的凸锥的边界是超平面或直线，所以也称为由 v1,v2,...,vm 张成的 凸多面锥。
定义3：(容许方向向量，容许方向锥) 设 D 是 Rn 中的非空集，且 x∈D ，对于非零向量 p∈Rn ，若存在 δ>0 ，当 t∈(0,δ) 时，必有 x+tp∈D ，则称 p 是点 x 的 容许方向向量，其方向称为点 x d的 容许方向。由点 x 的所有容许方向向量构成的集合称为点 x 的 容许方向锥。
引理3： 设 x~∈D={x|si(x~)≥0,i=1,2,...,m} ， I={i|si(x~)=0,i=1,2,...,m} ；并设 i∈I 时， si(x) 在点 x~ 处可微，当 i∉I 时， si(x) 在点 x~ 处连续。若向量 p 对于所有的 i∈I ，都有 ∇si(x~)Tp>0 ，则 p 是点 x~ 的一个容许方向向量。
通过引理3我们知道，若某一个容许点 x~ 近使某一个约束 si(x)≥0 变为起作用约束,而其他约束仍为不起作用约束时，可以知道 p=∇si(x~) 为点 x~ 处的容许方向向量。若容许点 x~ 使多个约束变为起作用约束，并记集合 I 为起作用约束的下标的集合，那么方向向量 p 若能使得所有的 ∇si(x~)Tp>0 ，此时 p 为容许方向向量。

定理4： 设 f:Rn→R1 在点 x 处可微，则点 x 处的下降方向向量 p 比满足

∇f(x)Tp<0

下面我们给出不等式约束最优性的几何最优性条件。
定理5： 在不等式约束最优化问题(3)中，若 x∗ 是局部最优点，则点 x∗ 处的容许方向锥和下降方向集是空集。
定理6： 在不等式约束最优化问题(3)中，假设：
(i) x∗ 是局部最优点， I={i|si(x∗)=0,i=1,2,...,m} ;
(ii) f(x) 在点 x∗ 处可微，当 x∉I 时， si(x) 在点 x∗ 连续。
那么，容许方向锥和下降方向集的交集为空。

定理5和定理6仅给出了必要的最优性条件，而没有充分最优性条件。为什么不是充分条件也许很难理解，其实这主要是针对于容许集中某些点可能存在容许方向锥是空集的情况，比如下面的例子。

mins.t.−x1−x21−x21−x22≥0−1+x21+x22≥0⎫⎭⎬⎪⎪

对于上式，所有的容许点(即在 x21+x22=1 上的点)均没有容许方向，所以必有容许方向锥和下降方向集的交集为空。所以容许方向锥和下降方向集的交集为空只是极小点的必要条件而不是充分条件。

Fritz John条件

首先介绍两个引理
引理7:(Farkas) 设 a1,a2,...,am 和 b 是n维向量，则满足

aTip≥0,i=1,2,...,m

的向量 p 也满足

bTp≥0

的充要条件是，存在非负数 γ1,γ2,...,γm ，使得

b=∑i=1mγiai

简单理解: 如下图所示，由于所有的 ai 都有 aTip<0 ，可以简单的认为所有的向量 ai 都在超平面 s1 的一侧，获得认为任意两个向量之间的夹角都要小于 π ，又由于 bTp≥0 ，所以向量 b 与向量 ai 都在超平面 s1 一侧，所以存在非负数 γi 使得杰伦成立。

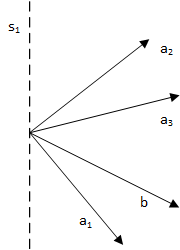
引理8：(Gordan) 设 a1,a2,...,am 和 b 是n维向量，则不存在向量 p 使得

aTip<0i=1,2,...,m

成立的充要条件是，存在不全为零的非负数 γ1,γ2,...,γm ，使得

∑i=1mγiai=0

简单理解: 根据引理8描述，我们知道必有向量 ai 使得 ai=−∑j≠iβjaj ，可以理解为下图。即存在一个超平面 s1 使得向量 si 分在超平面两侧；若所有向量 ai 都在超平面的一侧，必定存在另一条向量在超平面的另一侧使得 aTip<0 (表述有点问题，我是这么理解的)。

注: 上面的简单理解部分只是帮助理解这两个引理，并不正确，上面两个引理的证明比较繁琐，这里就不再证明。可以理解记忆，对于空间中的两个向量 a和b ，如果 aTb<0 ，则向量 a 和 b 的夹角为钝角；若 aTb>0 ，则夹角为锐角；若 aTb=0 ，则夹角为直角。下面给出FJ条件。

定理9：(Fritz John) 在不等式约束最优化问题(3)中，设 x∗ 是局部最优解， f(x) ， s1(x)，s2(x)，...，sm(x) 在点 x∗ 处可微。那么，存在不全为零的实数 μ0，μ1，...，μm ，使得

μ0∇f(x∗)−∑i=1mμi∇si(x∗)=0μisi(x∗)=0i=1,2,...,mμi≥0i=0,1,...,m⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪

证明: 由于 x∗ 是极小点，根据定理6我们知道，比不存在向量 p 使得

∇f(x∗)Tp<0

−∇si(x∗)Tp<0i∈I(I为起作用的约束下标集合)

根据引理8，可知必存在不全为零的数

μ0≥0μi≥0i∈I

使得

μ0∇f(x∗)−∑i∈Iμi∇si(x∗)=0

上式经过改写就是定理9(在定理9中，所有不起作用约束的 μi 均为0)。

对于FJ条件，我们可以这样理解。首先必须要清楚，定理9(FJ条件)是一个必要性条件，不是充分性条件，可以把定理9看作是定理6的一个数学描述。
(
其实，如果抛去必要性以及充分性，我们可以这么理解。根据FJ条件，假设 μ0 不为0，我们可以得到

∇f(x∗)=∑i∈Iμiμ0∇si(x∗)

由于 ∇f(x∗) 为函数 f(x) 的上升方面，对于任意容许方向向量 p ，必有

∇si(x∗)Tp≥0i∈I

因为约束条件为 si(x)≥0 ，所以对于在 x∗ 起作用的约束上式必然成立，因为上式成立所以也有 ∇f(x∗)≥0 成立，即对于所有的容许方向来说都不是下降方向。
这部分思考内容不一定正确，只是有助于自己的理解，这样思考也有助于记忆FJ条件会存在一些缺点，即 μ0 为0的时候，上面的思考就不成立。
)

Kuhn Tucker条件

其实，对于FJ条件，还是存在一定情况使得FJ条件失效的，加入对于在点 x∗ 处起作用的点的 ∇si(x∗) 是线性相关的的，即存在 μi 使得

∑i∈Iμi∇si(x∗)=0

，那么此时可以让 μ0=0 使得定理9仍然成立，但是计算出来的结果已经不是我找的最优解，此时FJ条件失去价值。若要求在 x∗ 处起约束作用的条件的 ∇si(x∗) 线性无关，便得到了KT条件。关于KT条件我们不在证明。

定理10：(Kuhn-Tucker) 在不等式约束最优化问题(3)中，假设:i) x∗ 是局部最优点；ii) f(x)，s1(x)，s2(x)，...，sm(x) 在点 x∗ 处可微；iii)点 x∗ 处全部起作用的约束线性无关。那么存在实数 μ0，μ1，...，μm ，使得

∇f(x∗)−∑i=1mμi∇si(x∗)=0μisi(x∗)=0i=1,2,...,mμi≥0i=1,2,...,m⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪

一般性约束最优性条件

关于一般性约束的FJ条件和KT条件，由于FJ条件的证明比较复杂，我们不给出证明；而KT条件可以参考不等式约束的KT条件。下面给出一般约束最优性FJ条件和KT条件的表述。
定理11：(Fritz John) 在约束最优化问题(1)中，设 x∗ 是局部最优解， f(x) ， s1(x)，s2(x)，...，sm(x);h1(x)，h2(x)，...，hl(x) 在点 x∗ 处可微。那么，存在不全为零的实数 μ0，μ1，...，μm;λ1，λ2，...，λl ，使得

μ0∇f(x∗)−∑i=1mμi∇si(x∗)−∑i=1lλi∇h(x∗)=0μisi(x∗)=0i=1,2,...,mμi≥0i=0,1,...,m⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪

定理12：(Kuhn-Tucker) 在约束最优化问题(1)中，假设:i) x∗ 是局部最优点；ii) f(x)，s1(x)，s2(x)，...，sm(x);h1(x)，h2(x)，...，hl(x) 在点 x∗ 处可微；iii)点 x∗ 处全部起作用的约束线性无关。那么存在实数 μ0，μ1，...，μm ，使得

∇f(x∗)−∑i=1mμi∇si(x∗)−∑i=1lλi∇h(x∗)=0μisi(x∗)=0i=1,2,...,mμi≥0i=1,2,...,m⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪