【机器学习实战】逻辑回归----sklearn库中的LogisticRegression类

LogisticRegression类

逻辑回归的基本思想在前面已经写过，就不再赘述。主要是为了了解并使用scikit-learn中逻辑回归类库，在实践前先整理一下里面的参数、属性和方法。
我们使用

##加载线性模型
from sklearn import linear_model
model=linear_model.LogisticRegression()

来加载逻辑回归模型。

【参数(Parameters)】

首先我们来看看LogisticRegression()有哪些参数。

penalty参数:

str, ‘l1’ or ‘l2’, default: ‘l2’
即选择正则化参数，str类型，可选L1和L2正则化，默认是L2正则化。

dual参数:

bool, default: False
即选择对偶公式(dual)或原始公式(primal)，bool类型默认是原始公式，当样本数大于特征数时，更倾向于原始公式，即False。

tol参数:

float, default: 1e-4
对停止标准的容忍，即求解到多少的时候认为已经求得最优解，并停止。float类型，默认值为1e-4。

C参数:

float, default: 1.0
设置正则化强度的逆，值越小，正则化越强。float类型，默认值为1.0。

fit_intercept参数:

bool, default: True
即选择是否将偏差(也称截距)添加到决策函数中。bool类型，默认为True，添加。

intercept_scaling参数:

float, default 1
只在solver选择liblinear并且self.fit_intercept设置为True的时候才有用。float类型。在这种情况下x变为 [ [ x,self.intercept_scaling ] ]

class_weight参数:

dict or ‘balanced’, default: None
即类型权重参数，用于标示分类模型中各种类型的权重。可以用字典模式输入也可选择‘balanced’模式，默认是None，即所有类型的权重都一样。
可以通过直接输入{class_label: weight}来对每个类别权重进行赋值，如{0:0.3,1:0.7}就是指类型0的权重为30%，而类型1的权重为70%。
也可以通过选择‘balanced’来自动计算类型权重，实际计算公式为：
n_samples / (n_classes * np.bincount(y))，当然这是不需要我们计算的啦。
在出现误分类代价很高或类别不平衡的情况下，我们可以通过这个参数来 在 出 现 误 分 类 代 价 很 高 或 类 别 不 平 衡 的 情 况 下 ， 我 们 可 以 通 过 这 个 参 数 来
调整权重。 调 整 权 重 。
1、误分类代价很高：比如说对合法用户和非法用户进行分类，将非法用户分 1 、 误 分 类 代 价 很 高 ： 比 如 说 对 合 法 用 户 和 非 法 用 户 进 行 分 类 ， 将 非 法 用 户 分
类为合法用户的代价很高，我们宁愿将合法用户分类为非法用户，这时可 类 为 合 法 用 户 的 代 价 很 高 ， 我 们 宁 愿 将 合 法 用 户 分 类 为 非 法 用 户 ， 这 时 可
以人工再甄别，但是却不愿将非法用户分类为合法用户。这时，我们可以 以 人 工 再 甄 别 ， 但 是 却 不 愿 将 非 法 用 户 分 类 为 合 法 用 户 。 这 时 ， 我 们 可 以
适当提高非法用户的权重。 适 当 提 高 非 法 用 户 的 权 重 。
2、类别不平衡：分类任务中不同类别的训练样例数目差别很大，这种情况 2 、 类 别 不 平 衡 ： 分 类 任 务 中 不 同 类 别 的 训 练 样 例 数 目 差 别 很 大 ， 这 种 情 况
在《机器学习》这本书中3.6节有提到，并且提出了“再缩放”的基本策略。 在 《 机 器 学 习 》 这 本 书 中 3.6 节 有 提 到 ， 并 且 提 出 了 “ 再 缩 放 ” 的 基 本 策 略 。

random_state参数:

int, RandomState instance or None, optional, default: None
随机数种子。仅在solver为‘sag’或者‘liblinear’时使用。int类型，默认为无。

solver参数:

{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’},
即选择逻辑回归损失函数优化算法的参数。默认情况是使用‘liblinear’算法。
对于小型数据集来说，选择‘liblinear’更好；对于大型数据集来说，‘saga’或者‘sag’会更快一些。
对于多类问题我们只能使用‘newton-cg’, ‘sag’, ‘saga’ and ‘lbfgs’。
对于正则化来说，‘newton-cg’,‘lbfgs’和‘sag’只能用于L2正则化(因为这些优化算法都需要损失函数的一阶或者二阶连续导数，因此无法用于没有连续导数的L1正则化)；而‘liblinear’,‘saga’则可处理L1正则化。
‘newton-cg’是牛顿家族中的共轭梯度法，‘lbfgs’是一种拟牛顿法， ‘newton-cg’是牛顿家族中的共轭梯度法，‘lbfgs’是一种拟牛顿法，
‘sag’则是随机平均梯度下降法，‘saga’是随机优化算法，‘liblinear’ ‘sag’则是随机平均梯度下降法，‘saga’是随机优化算法，‘liblinear’
是坐标轴下降法 是坐标轴下降法

max_iter参数:

int, default: 100
算法收敛最大迭代次数，int类型，默认为100。
只在solver为‘newton-cg’，‘sag’和‘lbfgs’是有用。

multi_class参数:

str, {‘ovr’, ‘multinomial’}, default: ‘ovr’
即选择分类方式的参数，可选参数有‘ovr’和‘multinomial’，str类型，默认为‘ovr’。
‘ovr’即one-vs-rest(OvR)，而‘multinomial’即many-vs-many(MvM)。
OvR每次将一个类的样例作为正例，所有其他类的样例作为反例来训练， O v R 每 次 将 一 个 类 的 样 例 作 为 正 例 ， 所 有 其 他 类 的 样 例 作 为 反 例 来 训 练 ，
在测试中若仅有一个分类器预测为正类，则对应的类别标记为最终结果； 在 测 试 中 若 仅 有 一 个 分 类 器 预 测 为 正 类 ， 则 对 应 的 类 别 标 记 为 最 终 结 果 ；
若有多个分类器预测为正类，则考虑每个分类器的置信度，置信度高的 若 有 多 个 分 类 器 预 测 为 正 类 ， 则 考 虑 每 个 分 类 器 的 置 信 度 ， 置 信 度 高 的
类别作为分类结果 类 别 作 为 分 类 结 果
MvM则是每次将若干类作为正例，若干其他类作为反例 M v M 则 是 每 次 将 若 干 类 作 为 正 例 ， 若 干 其 他 类 作 为 反 例

verbose参数:

int, default: 0
日志冗长度；对于solver为‘liblinear’和‘lbfgs’将详细数字设置为任意正数以表示详细；int类型。默认为0。

warm_start参数:

bool, default: False
热启动参数；bool类型，默认为False。当设置为True时，重用上一次调用的解决方案作为初始化，否则，只需删除前面的解决方案。对于‘liblinear’没用。

n_jobs参数:

int, default: 1
并行数。int类型，默认为1，代表CPU的一个内核运行程序。

【属性(Attributes)】

与线性回归模型类似，有coef_(决策函数中的特征系数)，intercept_(决策函数的偏置)和n_iter_(所有类的实际迭代次数)。最常用的就是coef_和intercept_。

【方法(Methods)】

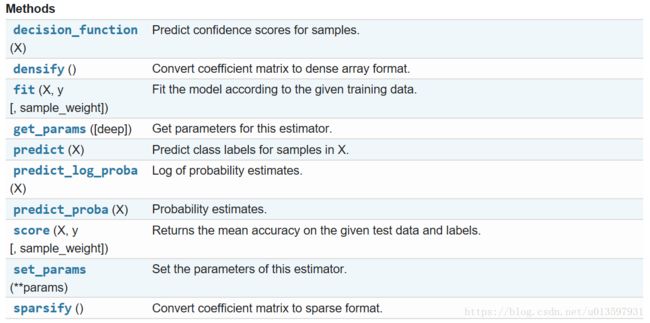
fit()、predict()、score()是经常会用到的。
fit()用于根据给定的数据拟合模型，predict()一般会传入测试样本然后得到预测值，score()用于评价模型，这里用的是平均精确度。

参考：
http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression

http://www.cnblogs.com/pinard/p/6035872.html