协方差、PCA、样本中心化,白化、方差、标准差、BN
协方差
度量各个维度偏离其均值的程度。协方差的值如果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),结果为负值就说明负相关的,如果为0,也是就是统计上说的“相互独立”。
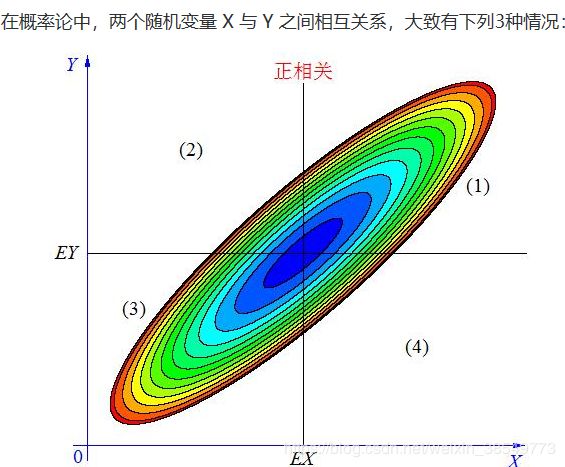
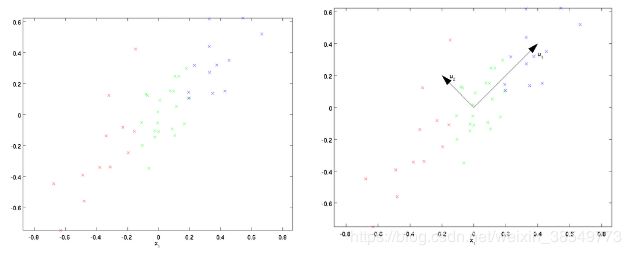
当 X, Y 的联合分布像上图那样时,我们可以看出,大致上有: X 越大 Y 也越大, X 越小 Y 也越小,这种情况,我们称为“正相关”。
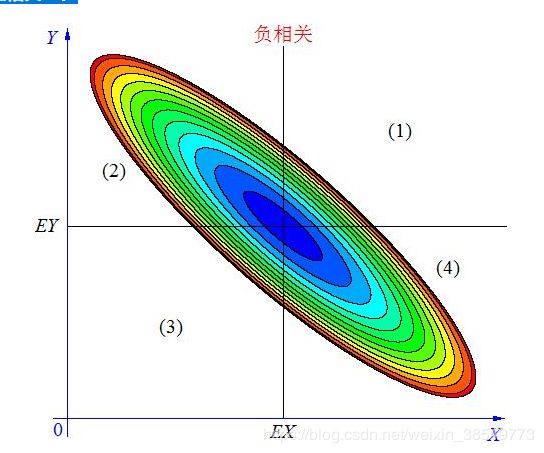
当X, Y 的联合分布像上图那样时,我们可以看出,大致上有:X 越大Y 反而越小,X 越小 Y 反而越大,这种情况,我们称为“负相关”。
当X, Y 的联合分布像上图那样时,我们可以看出:既不是X 越大Y 也越大,也不是 X 越大 Y 反而越小,这种情况我们称为“不相关”。
在图中的区域(1)中,有 X>EX ,Y-EY>0 ,所以(X-EX)(Y-EY)>0;在图中的区域(2)中,有 X
————————————————
版权声明:本文为CSDN博主「GoodShot」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/GoodShot/article/details/79940438
主成分分析(PCA)
PCA和LDA都是对数据进行降维,其中PCA是无监督的,LDA是有监督的。所以PCA是不考虑类别的,只用特征信息,而LDA要考虑类别
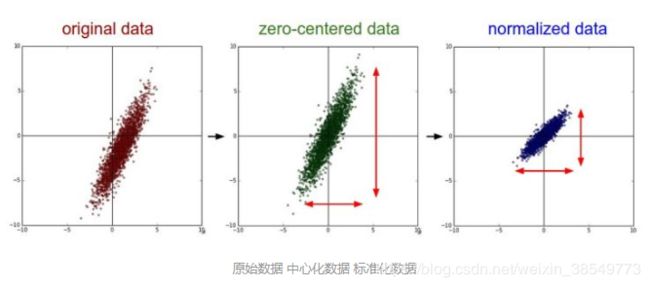
对样本进行中心化
中心化其实是一个平移的过程,平移后所有数据的中心是(0,0)
在PCA中,中心化后的数据有助于后续在求协方差的步骤中减少计算量,同时中心化后的数据才能比较好地“概括”原来的数据(如下图)
原文链接:https://www.jianshu.com/p/1518369c2c61
白化
白化的目的是去除输入数据的冗余信息。
例如:训练数据是图像,由于图像中相邻像素之间具有很强的相关性,因此输入是冗余的。白化的目的就是降低输入的冗余性。
输入数据集,经过白化处理后,生成的新数据集满足两个条件:一是特征相关性较低;二是特征具有相同的方差
白化算法的实现过程:第一步操作是PCA,求出新特征空间中的新坐标,第二步是对新的坐标进行方差归一化操作。
白化分为PCA白化、ZCA白化
PCA预处理:
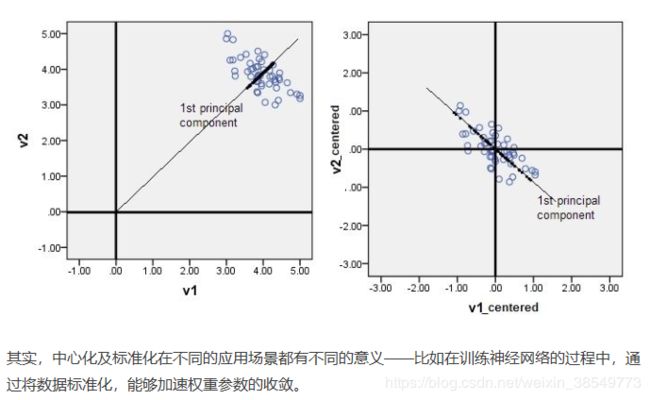
左图表示原始数据X,然后我们通过协方差矩阵可以求得特征向量u1、u2,然后把每个数据点,投影到这两个新的特征向量(这两个特征向量是不变且正交的),得到进行坐标如下:
(变换数据坐标中心)这就是pca处理。
PCA白化
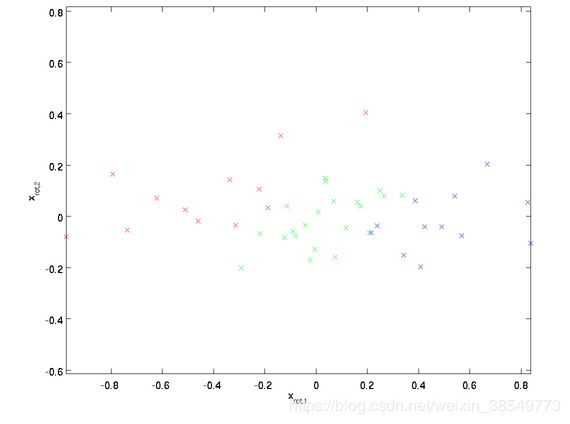
pca白化是指对上面的pca的新坐标X’,每一维的特征做一个标准差归一化处理。从上面我们看到在新的坐标空间中,(x1,x2)两个坐标轴方向的数据明显标准差不同,因此我们接着要对新的每一维坐标做一个标注差归一化处理。
ZCA白化
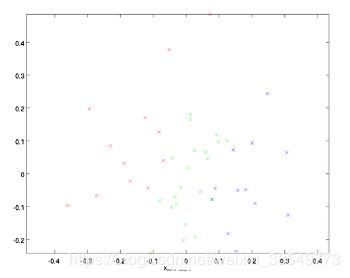
ZCA白化是在PCA白化的基础上,把上面PCA白化的结果,又变换到原来坐标系下的坐标
方差是各个数据与平均数之差的平方的和的平均数
标准差(Standard Deviation)又常称均方差
BN
BN其实就是把每个隐层神经元的激活输入分布从偏离均值为0方差为1的正态分布通过平移均值压缩或者扩大曲线尖锐程度,调整为均值为0方差为1的正态分布。
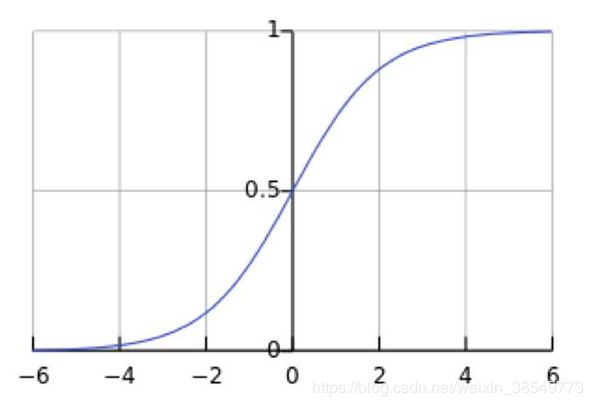
这意味着在一个标准差范围内,也就是说64%的概率x其值落在[-1,1]的范围内,在两个标准差范围内,也就是说95%的概率x其值落在了[-2,2]的范围内。那么这又意味着什么?我们知道,激活值x=WU+B,U是真正的输入,x是某个神经元的激活值,假设非线性函数是sigmoid,那么看下sigmoid(x)其图形:
原文:https://blog.csdn.net/guo1988kui/article/details/83794343