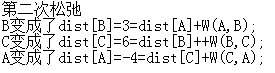最短路径
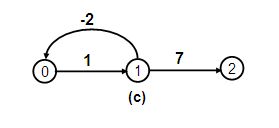
方法:求解边上带有负值的单源最短路径问题,从源点逐次通过其他顶点,以缩短到达终点的最短路径长度。
限制条件:不能包含权值总和为负值回路(负权值回路),不然会在一个回路中一直负循环下去
理解一:Bellman-Ford(贝尔曼-福特)
构建图的邻接矩阵Edge[ i ][ j ]=w,表示从 i 到 j 权值为w,构造一个最短路径长度数组序列dist (1) [u],dist(2) [u] …, dist (n-1)[u]。
dist (1) [u]表示从源点到终点U的只经过一条边的最短路径长度,dist 2 [U] 表示从源点V最多经过两条边到达终点U的最短路径,最终计算出dist n-1 [U]。
| k |
dist(k)[0] |
dist(k)[1] |
dist(k)[2] |
dist(k)[3] |
dist(k)[4] |
dist(k)[5] |
dist(k)[6] |
| 1 |
0 |
6 |
5 |
5 |
∞ |
∞ |
∞ |
| 2 |
0 |
3 |
3 |
|
|
|
|
| 3 |
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
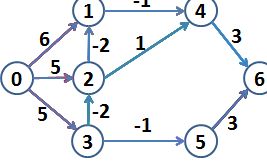
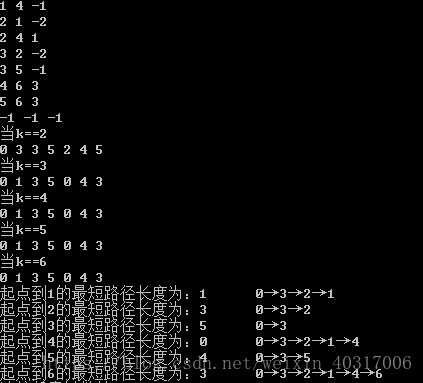
以上图解:k表示从源点到其他的点最多经过k条路的最短距离dist[k]。
k=1:0点到其他U点的距离为Edge[0][U],所以分别为 0 6 5 5 ∞ ∞ ∞。
k=2:最多两条边的情况下,dist(2)[0]=min{dist(1)[0],dist(i)+Edge[i][0],(i=1,2,3,4,5,6)}。0->0仍为0,
0->1相当于0->2->1为3,(3比原来dist[1]小),dist(2)[1]=min{dist(1)[1],dist(i)+Edge[i][1],(i=0,2,3,4,5,6)}
0->2相当于dist(2)[2]=min{dist(1)[2],dist(i)+Edge[i][2],(i=0,1,3,4,5,6)} ...以此类推
k=3:最多三条边情况下,0->1相当于dist(3)[1]=min{dist(2)[1],dist(i)+Edge[i][1],(i=0,2,3,4,5,6)}
...以上每个点都是以此类推,得到公式(求顶点u到源点v的最短路径)
dist 1 [u] = Edge[v][u]
dist k [u] = min{ dist k-1 [u], min{ dist k-1 [j] + Edge[j][u] } }, j=0,1,…,n-1,j≠u
第一条是当K=1,源点到其他点只走一条路的最短路径。第二条的意思是,dist[u],在最多走K条路的情况下,是原dist[u]的路径比较小,还是在最多走K-1条路到点j的最短路径加上j到u权值的最短路径小。j为除了本身u以外的其他点。
#include
#include
using namespace std;
#define INF 1000000 //无穷大
#define MAXN 20 //顶点个数最大值
int n; //顶点个数
int Edge[MAXN][MAXN]; //邻接矩阵
int dist[MAXN]; //
int path[MAXN]; //
void Bellman (int v0);
int main()
{
cin>>n;
while(1) //构建邻接矩阵
{
int u,v,w;
cin>>u>>v>>w;
if(u==-1 && v==-1 && w==-1)
break;
Edge[u][v]=w;
}
for (int i = 0; i0; j--)
printf("%d→", shortest[j]);
printf("%d\n", shortest[0]);
}
}
void Bellman (int v0)
{
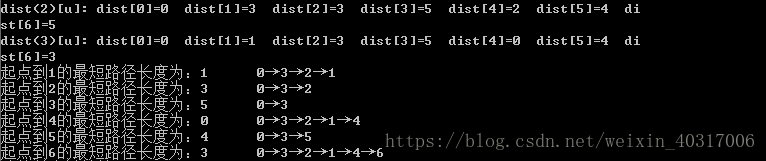
for(int i=0;i 为什么在k=k的情况下,跟我们分析的数据不一样呢?那是因为dist[u]是一维数组,k=0...的时候,存放的是dist(k-1)[u]的数据,在这个数组中会直接被更新,所以当数组不再被更新的时候,可以提前结束这个三重循环。
for (int k = 2; k思想二:SPFA(算法)
其实跟思想一是没有特别大的区别。但是以边的结构体来存并不用邻接矩阵
第一,初始化所有点。dist[u]将原点的值设为0,其它的点的值设为无穷大(表示不可达)。
第二,进行循环,循环下标为从1到n-1(n等于图中点的个数)。在循环内部,遍历所有的边,进行松弛计算。
第三,遍历途中所有的边(edge(u,v)),判断是否存在这样情况:d(v) > d (u) + w(u,v) 存在则返回false,表示途中存在从源点可达的权为负的回路。这里是为了检查如果存在从源点可达的权为负的回路。则应为无法收敛而导致不能求出最短路径。
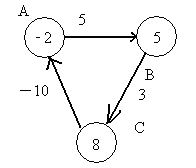
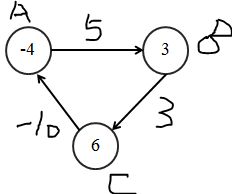
第二次遍历后,正是因为有一条负边在回路中,导致每次遍历后,各个点的值不断变小。在回过来看一下bellman-ford算法的第三部分,遍历所有边,检查是否存在d(v) > d (u) + w(u,v)。因为第二部分循环的次数是定长的,所以如果存在无法收敛的情况,则肯定能够在第三部分中检查出来。比如,点A的值为-2,点B的值为5,边AB的权重为5,5 > -2 + 5. 检查出来这条边没有收敛。
struct Edge
{
int u; //起点
int v; //终点
int w; //权值
};
void Bellman (int v0)
{
int n,m;
//n为定点个数,m为边的条数
for(int i=0;i dist[Edge[i].u] + Edge[i].w)
{
flag = 0;
break;
}
return flag;
}
思路三:Bellman-Ford算法改进SPFA(算法)
前面两种都是以边来实施,而这个是以点来实施。用一个队列来维护,初始时将源点加入队列,每次从队列中取出一个顶点,并对所有与它相邻的顶点进行松弛,若某个相邻的顶点松弛成功,则将其入队。重复这样的过程直到队列为空时算法结束。
https://blog.csdn.net/xunalove/article/details/70045815
【过程】
![]()