机器学习实战(11) 利用PCA来简化数据 基于python3

PCA理论

PCA(主成分分析)是一种降维技术，其他两种降维技术是因子分析和独立成分分析。
loaddata函数导入数据；pca函数首先去平均值，然后获取去均值后的协方差矩阵，计算协方差矩阵的特征值和特征向量，然后将数据转换到新空间。

def loaddata(filename,delim='\t'):
    with open(filename) as fr:
        arr = [line.strip().split(delim) for line in fr.readlines()]
    dataarr = np.array(arr).astype(float)
    return dataarr
def pca(data,nfeat=9999999):
    meanval = np.mean(data,0)
    meanre = data - meanval
    #此处会获取一个2x2协方差矩阵
    covmat = np.cov(meanre,rowvar=False)#rowvar为0 行代表一条数据，列代表一个特征 默认为True
    eigval,eigvect = np.linalg.eig(covmat)
    eigvalind = np.argsort(eigval)#获取排序后的索引
    eigvalind = eigvalind[:-(nfeat+1):-1]#倒序，取倒序的前nfeat个
    redeigvect = eigvect[:,eigvalind]
    lowdat = np.dot(meanre,redeigvect)
    recon = np.dot(lowdat,redeigvect.T) + meanval
    return lowdat,recon

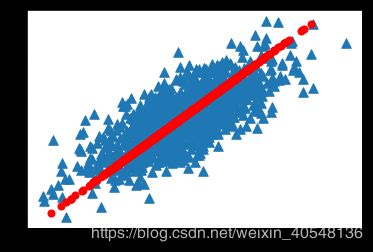
我们来看下pca运行结果

data = loaddata(filename1)
lowdat,recon = pca(data,1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(data[:,0],data[:,1],marker='^',s=90)
ax.scatter(recon[:,0],recon[:,1],marker='o',s=50,c='red')
plt.show()

利用PCA对半导体制造数据降维

这里我们首先对数据预处理，将nan替换成平均值的函数。
然后重复前面的pca流程。

def replacenan():
    data2 = loaddata(filename2,' ')
    numfeat = data2.shape[1]
    for i in range(numfeat):
        meanval = np.mean(data2[np.nonzero(~np.isnan(data2[:,i]))[0],i])#~np.isnan()取nan的值
        data2[np.nonzero(np.isnan(data2[:,i]))[0],i] = meanval
    return data2
data2 = replacenan()
print(data2)
meanval = np.mean(data2,axis=0)
meanre = data2 - meanval

cova = np.cov(meanre,rowvar=0)

eigval,eigvect = np.linalg.eig(cova)

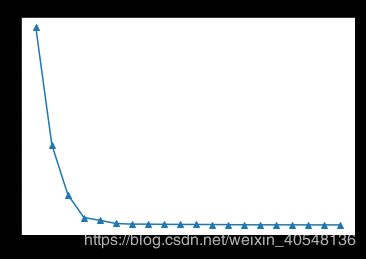
查看eigval我们发现超过20%的特征值都是0，最前面15个值的数量级大于$10^5$，之后的值变得非常小，前20个主成分覆盖了99.3%的方差。