【网易】矩形重叠 、牛牛的背包、小易的字典 — C++

矩形重叠：

题目描述：
平面内有n个矩形, 第i个矩形的左下角坐标为(x1[i], y1[i]), 右上角坐标为(x2[i], y2[i])。 
如果两个或者多个矩形有公共区域则认为它们是相互重叠的(不考虑边界和角落)。 
请你计算出平面内重叠矩形数量最多的地方,有多少个矩形相互重叠。 

输入描述:
输入包括五行。
第一行包括一个整数n(2 <= n <= 50), 表示矩形的个数。
第二行包括n个整数x1[i](-10^9 <= x1[i] <= 10^9),表示左下角的横坐标。
第三行包括n个整数y1[i](-10^9 <= y1[i] <= 10^9),表示左下角的纵坐标。
第四行包括n个整数x2[i](-10^9 <= x2[i] <= 10^9),表示右上角的横坐标。
第五行包括n个整数y2[i](-10^9 <= y2[i] <= 10^9),表示右上角的纵坐标。

输出描述:
输出一个正整数, 表示最多的地方有多少个矩形相互重叠,如果矩形都不互相重叠,输出1。

输入:
2
0 90
0 90
100 200
100 200

输出:
2

如何判断矩形是否重叠？

 第一种：正向思维

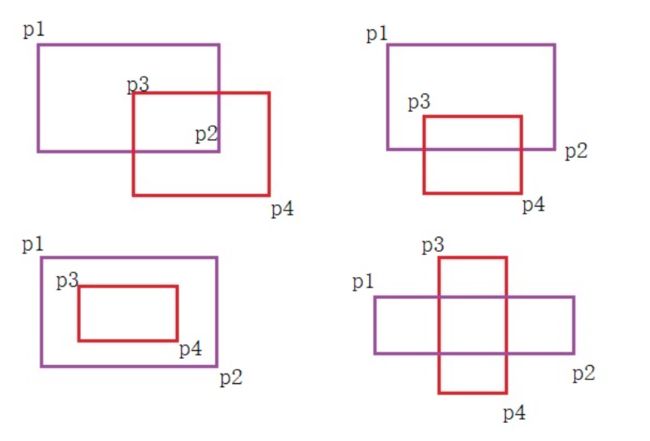
   按照一般的思路，先列举出所有的矩形重叠的情况，然后，判断是否是其中一种，如图所示，共有四种重叠情况，我们使用紫色代表矩形A，红色代表矩形B，并分别用p1,p2,p3,p4代表对应的左上角与右下角。如果依次判断，过于复杂，而且容易出错。

 

第二种：逆向思维 

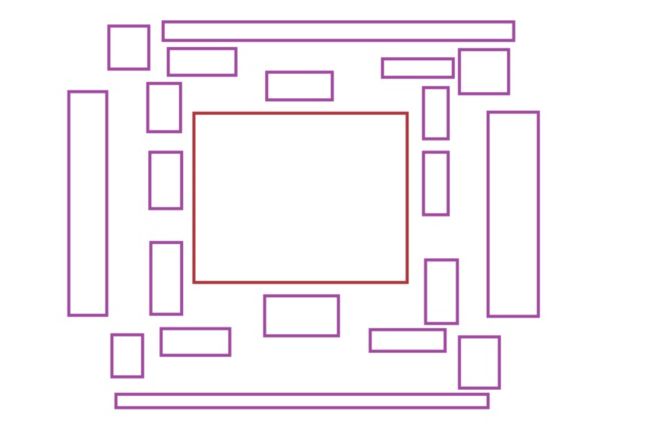
   我们不妨先解决出“不重叠”的情况，如图，我们画出了一个并怎么漂亮的图，看起来十分复杂，但是，实际上，相比第一种方案，更易表示。即B矩阵，可能在A的左侧、右侧、上侧、下侧。如果用公式表示，即： (p2.y≤p3.y)∨(p1.y≥p4.y)∨(p2.x≤p3.x)∨(p1.x≥p4.xp2.y≤p3.y)∨(p1.y≥p4.y)∨(p2.x≤p3.x)∨(p1.x≥p4.x) ，则，两个矩阵重叠时，公式为 ：¬[(p2.y≤p3.y)∨(p1.y≥p4.y)∨(p2.x≤p3.x)∨(p1.x≥p4.x)]¬[(p2.y≤p3.y)∨(p1.y≥p4.y)∨(p2.x≤p3.x)∨(p1.x≥p4.x)]

  根据德·摩根定律可转换为 ：

(p2.y>p3.y)∧(p1.yp3.x)∧(p1.xp3.y)∧(p1.yp3.x)∧(p1.x

 

在本题中，要计算出平面内重叠矩形数量最多的地方,有多少个矩形相互重叠，那么看作点最多被多少矩形包围！

#include 
#include 
#include 
using namespace std;

class rectangle
{
public:
	int l_x;
	int l_y;
	int r_x;
	int r_y;
	rectangle(int a, int b, int c, int d): l_x(a), l_y(b), r_x(c), r_y(d){} 
}; 
int main() 
{ 
	int n;
	scanf("%d", &n);
	vector lX(n); //矩形左下角坐标
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &lX[i]);
	}
	vector lY(n); 
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &lY[i]);
	}
	vector rX(n);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &rX[i]);
	}
	vector rY(n);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &rY[i]);
	}
	vector ARectangle; //vector中存放所有的rectangle类坐标
	for (int i = 0; i < n; i++)
	{
		ARectangle.push_back(rectangle(lX[i], lY[i], rX[i], rY[i]));
	}
	vector X; //所有X点
	for (int i = 0; i < n; i++)
	{  
		X.push_back(lX[i]);
		X.push_back(rX[i]); 
	}
	vector Y; //所有Y点
	for (int i = 0; i < n; i++)
	{ 
		Y.push_back(lY[i]);
		Y.push_back(rY[i]); 
	}
	int count = 0, res = 0; 
	for (int i = 0; i < X.size(); i++)
	{ 
		for (int j = 0; j < Y.size(); j++)
		{   //点被最多的矩形包围则说明矩形重叠个数最多；
			for (int k = 0; k < ARectangle.size(); k++)
			{  //反证 //A矩形位于B矩形上侧，下侧，左侧，右侧；
			   //证明重叠
				if (X[i] >= ARectangle[k].l_x && X[i] < ARectangle[k].r_x &&
					Y[j] >= ARectangle[k].l_y && Y[j] < ARectangle[k].r_y)
				{
					count ++; 
				}
			} 
			res = max(res, count);
			count = 0; 
		}
	}
	cout<

 参考：(๑•̀ㅂ•́)و✧ https://blog.csdn.net/qianchenglenger/article/details/50484053

牛牛的背包问题： 

题目描述：
牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容量为w。 
牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。 
牛牛想知道在总体积不超过背包容量的情况下,他一共有多少种零食放法(总体积为0也算一种放法)。 

输入描述:
输入包括两行
第一行为两个正整数n和w(1 <= n <= 30, 1 <= w <= 2 * 10^9),表示零食的数量和背包的容量。
第二行n个正整数v[i](0 <= v[i] <= 10^9),表示每袋零食的体积。

输出描述:
输出一个正整数, 表示牛牛一共有多少种零食放法。

输入
3 10
1 2 4

输出
8

说明
三种零食总体积小于10,于是每种零食有放入和不放入两种情况，一共有2*2*2 = 8种情况。

利用动态规划实现!

#include 
#include 
#include 
using namespace std;

int n;
long w;
long ans = 0; //计数器
vector vec;
void dfs(long sum,int loc);

int main()
{
    long total = 0;
    cin >> n;
    cin >> w;
    for(int i = 0;i < n;++i)
    {
        int x;
        cin >> x;
        vec.push_back(x);
        total += vec[i]; //所有放进去都成立
    }
    if(total <= w)
    {
        ans = pow(2,n);
    }
    else
    {
        sort(vec.begin(),vec.end());
        dfs(0,0);
    }
    cout << ans << endl;
    
    return 0;
}                                //dfs(0,0)       dfs(0,1)       dfs(0,2)
void dfs(long sum,int loc)       // 1 2 4       // 1 2 4       // 1 2 4  
{                                // 1      1    // 2      4         
    if(sum > w)                  // 1+2    2    // 2+4    5
        return ;                 // 1+2+4  3    
    if(sum <= w)
        ans++;
    for(int i = loc;i < n;++i)
    {
        dfs(sum+vec[i],i+1); //不断递归
    }
}

 小易的字典

题目描述
小易在学校中学习了关于字符串的理论, 于是他基于此完成了一个字典的项目。 
小易的这个字典很奇特, 字典内的每个单词都包含n个'a'和m个'z', 并且所有单词按照字典序排列。 
小易现在希望你能帮他找出第k个单词是什么。 

输入描述:
输入包括一行三个整数n, m, k(1 <= n, m <= 100, 1 <= k <= 109), 以空格分割。

输出描述:
输出第k个字典中的字符串，如果无解，输出-1。 

输入
2 2 6

输出
zzaa

说明
字典中的字符串依次为aazz azaz azza zaaz zaza zzaa

#include 
#include 
#include 
#include 
using namespace std;

class Solution{
public:
    void solve(int n,int m,long long k)
    {
        vector x;
        while(n && m)
        {
            //每次迭代问题规模缩减一个单位
            ////排列组合:假设当前序列首字符为a，剩下n-1个a放在剩下n - 1 +m 个位置共有的可能数
            long long count = 1;
            for(int i = 0;i < n-1;++i)
            {
                //求组合数
                count *= n-1+m-i;
                count /= (i+1);
                if(count > k) break;
                //防止越界。count>k就可以退出计算了
            }
            if(k <= count)
            {  //如果k小于等于count，则表明首字符的确应为a
                x.push_back('a');
                n--; //问题缩减为 n-1个a和m个z 中找第k大
            }
            else
            {
                x.push_back('z');
                m--; //问题缩减为 n-1个a和m个z 中找第k-count大
                k -= count;
            }
        }
        //循环结束后，剩余子序列只存在"aa..aaa" 或 "zz..zzz"1种情况
        if(k != 1)
        {
            cout << -1;
            return ;
        }
        while(n--) x.push_back('a');
        while(m--) x.push_back('z');
        for(int i = 0;i < x.size();++i)
        {
            cout << x[i];
        }
    }
};


int main()
{
    Solution a;
    int n,m;
    long long k;
    while(cin >> n >> m >> k)
    {
        a.solve(n,m,k);
    }
    
    return 0;
}

 代码参考：(๑•̀ㅂ•́)و✧ https://www.nowcoder.com/questionTerminal/12b1b8ef17e1441f86f322b250bff4c0