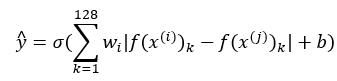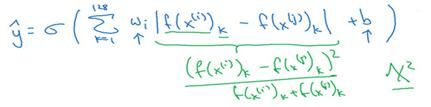吴恩达深度学习笔记(105)-人脸识别之面部验证与二分类

https://www.toutiao.com/a6652895489354105351/

 

面部验证与二分类（Face verification and binary classification）

Triplet loss是一个学习人脸识别卷积网络参数的好方法，还有其他学习参数的方法，让我们看看如何将人脸识别当成一个二分类问题。

 

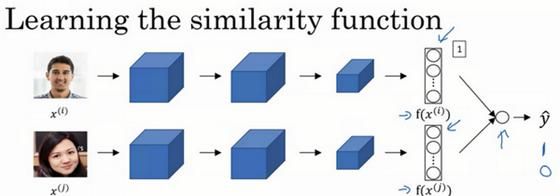
另一个训练神经网络的方法是选取一对神经网络，选取Siamese网络，使其同时计算这些嵌入，比如说128维的嵌入（编号1），或者更高维，然后将其输入到逻辑回归单元，然后进行预测，如果是相同的人，那么输出是1，若是不同的人，输出是0。

这就把人脸识别问题转换为一个二分类问题，训练这种系统时可以替换Triplet loss的方法。

最后的逻辑回归单元是怎么处理的？

输出y^会变成，比如说sigmoid函数应用到某些特征上，相比起直接放入这些编码（f(x^(i)),f(x^(j))），你可以利用编码之间的不同。

 

我解释一下，符号f(x^(i) )_k代表图片x^(i)的编码，下标k代表选择这个向量中的第k个元素，|f(x^(i) )_k-f(x^(j) )_k |对这两个编码取元素差的绝对值。

你可能想，把这128个元素当作特征，然后把他们放入逻辑回归中，最后的逻辑回归可以增加参数w_i和b，就像普通的逻辑回归一样。你将在这128个单元上训练合适的权重，用来预测两张图片是否是一个人，这是一个很合理的方法来学习预测0或者1，即是否是同一个人。

 

还有其他不同的形式来计算绿色标记的这部分公式（|f(x^((i)) )_k-f(x^((j)) )_k |），

比如说，公式可以是((f(x^((i)) )_k-f(x^((j)) )_k )^2)/(f(x^((i)) )_k+f(x^((j)) )_k )，

这个公式也被叫做χ^2公式，是一个希腊字母χ，也被称为χ平方相似度。

	Yaniv Taigman, Ming Yang, Marc'Aurelio Ranzato, Lior Wolf (2014). DeepFace: Closing the gap to human-level performance in face verification

这些公式及其变形在这篇DeepFace论文中有讨论，之前也引用过。

 

但是在这个学习公式中，输入是一对图片，这是你的训练输入x（编号1、2），输出y是0或者1，取决于你的输入是相似图片还是非相似图片。

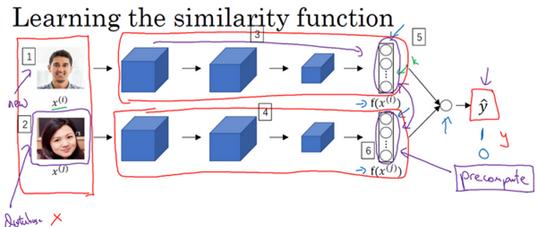
与之前类似，你正在训练一个Siamese网络，意味着上面这个神经网络拥有的参数和下面神经网络的相同（编号3和4所示的网络），两组参数是绑定的，这样的系统效果很好。

之前提到一个计算技巧可以帮你显著提高部署效果，如果这是一张新图片（编号1），当员工走进门时，希望门可以自动为他们打开，这个（编号2）是在数据库中的图片，不需要每次都计算这些特征（编号6），不需要每次都计算这个嵌入，你可以提前计算好，那么当一个新员工走近时，你可以使用上方的卷积网络来计算这些编码（编号5），然后使用它，和预先计算好的编码进行比较，然后输出预测值y^。

因为不需要存储原始图像，如果你有一个很大的员工数据库，你不需要为每个员工每次都计算这些编码。这个预先计算的思想，可以节省大量的计算，这个预训练的工作可以用在Siamese网路结构中，将人脸识别当作一个二分类问题，也可以用在学习和使用Triplet loss函数上，我在之前的视频中描述过。

总结一下，把人脸验证当作一个监督学习，创建一个只有成对图片的训练集，不是三个一组，而是成对的图片，目标标签是1表示一对图片是一个人，目标标签是0表示图片中是不同的人。利用不同的成对图片，使用反向传播算法去训练神经网络，训练Siamese神经网络。

 

这个你看到的版本，处理人脸验证和人脸识别扩展为二分类问题，这样的效果也很好。

希望你知道，在一次学习时，你需要什么来训练人脸验证，或者人脸识别系统