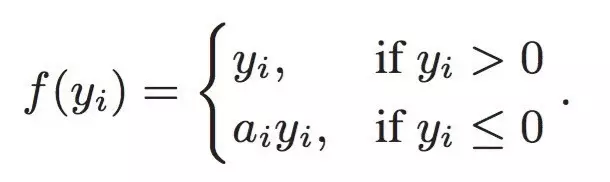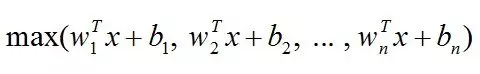为什么使用非线性激活函数？常见的非线性激活函数及优缺点对比

• 为何使用非线性激活函数？ 

​

 如上图的神经网络，在正向传播过程中，若使用线性激活函数(恒等激励函数)，即令，则隐藏层的输出为

 

 即

 

可以看到使用线性激活函数神经网络只是把输入线性组合再输出，所以当有很多隐藏层时，在隐藏层使用线性激活函数的训练效果和不使用影藏层即 标准的Logistic回归是一样的。故我们要在隐藏层使用非线性激活函数而非线性的。

通常只有一个地方可以使用线性激活函数，就是你在做机器学习中的回归问题。 y是一个实数，举个例子，比如你想预测房地产价格， y就不是二分类任务0或1，而是一个实数，从0到正无穷。如果y是个实数，那么在输出层用线性激活函数也许可行，你的输出也是一个实数，从负无穷到正无穷。总而言之，不能在隐藏层使用线性激活函数，除了一些特殊情况，比如和压缩有关的。

• 饱和的概念

当一个激活函数h(x)满足时，我们称之为右饱和。 
当一个激活函数h(x)满足 时，我们称之为左饱和。 
当一个激活函数，既满足左饱和又满足又饱和时，我们称之为饱和。

对任意的x，如果存在常数c，当 x > c 时恒有则称其为右硬饱和。 
对任意的x，如果存在常数c，当 x < c 时恒有则称其为左硬饱和。 
若既满足左硬饱和，又满足右硬饱和，则称这种激活函数为硬饱和。 
如果只有在极限状态下偏导数等于0的函数，称之为软饱和。

•  常用激活函数

参考链接：

1）https://mp.weixin.qq.com/s？__biz=MzI1NTE4NTUwOQ==&mid=2650325236&idx=1&sn=7bd8510d59ddc14e5d4036f2acaeaf8d&scene=0#wechat_redirect

2）http://www.ai-start.com/dl2017/html/lesson1-week3.html#header-n152

1、sigmoid函数

 

 求导：

当或：

 当： 

  Sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。由于在后向传递过程中，sigmoid向下传导的梯度包含了一个f’(x) 因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f’(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。

优点：

1. Sigmoid 函数的输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可以用作输出层。它在物理意义上最为接近生物神经元。
2. 求导容易。

缺点：

1. 由于其软饱和性，容易产生梯度消失，导致训练出现问题。
2. 其输出并不是以0为中心的。

 2、tanh  

同样的，Tanh 激活函数也具有软饱和性。Tanh 网络的收敛速度要比 Sigmoid 快。因为 Tanh 的输出均值比 Sigmoid 更接近 0，SGD 会更接近 natural gradient（一种二次优化技术），从而降低所需的迭代次数。

优点：

1. 比Sigmoid函数收敛速度更快。
2. 相比Sigmoid函数，其输出以0为中心。

缺点：

      还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失。

 3、Relu与Leeaky Relu

 ReLU 在x<0 时硬饱和。由于 x>0时导数为 1，所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。但随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为“神经元死亡”。

优点：

1. 相比起Sigmoid和tanh，ReLU在SGD中能够快速收敛。据称，这是因为它线性、非饱和的形式。
2. Sigmoid和tanh涉及了很多很expensive的操作（比如指数），ReLU可以更加简单的实现。
3. 有效缓解了梯度消失的问题。
4. 在没有无监督预训练的时候也能有较好的表现。
5. 提供了神经网络的稀疏表达能力。

缺点：

        随着训练的进行，可能会出现神经元死亡，权重无法更新的情况。如果发生这种情况，那么流经神经元的梯度从这一点开始将永远是0。也就是说，ReLU神经元在训练中不可逆地死亡了。

        ReLU另一个问题是输出具有偏移现象，即输出均值恒大于零。偏移现象和 神经元死亡会共同影响网络的收敛性。

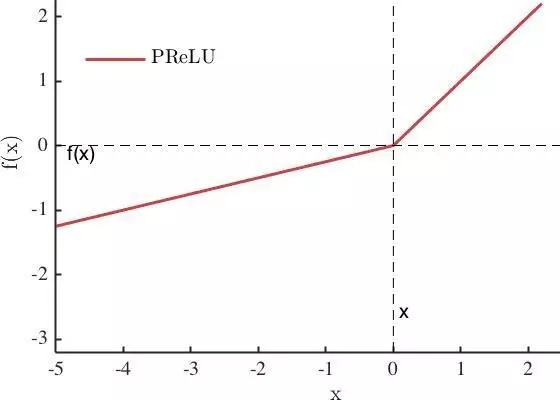
4、PRelu

PReLU 是 ReLU 和 LReLU 的改进版本，具有非饱和性。当 ai 比较小且固定的时候，称之为 LReLU。LReLU 最初的目的是为了避免梯度消失。但在一些实验中，发现 LReLU 对准确率并没有太大的影响。很多时候，当我们想要应用 LReLU 时，必须非常小心谨慎地重复训练，选取出合适的 a，LReLU 表现出的结果才比 ReLU 好。因此有人提出了一种自适应地从数据中学习参数的 PReLU。PReLU具有收敛速度快、错误率低的特点。因为PReLU的输出更接近0均值，使得SGD更接近natural gradient。PReLU可以用于反向传播的训练，可以与其他层同时优化。

5、Erelu

ELU 融合了sigmoid和ReLU，具有左侧软饱性。右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱能够让ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于零，所以收敛速度更快。

PReLU、ELU等激活函数不具备Relu这种稀疏性，但都能够提升网络性能。

6、Maxout

Maxout是ReLU的推广，其发生饱和是一个零测集事件。Maxout网络能够近似任意连续函数，且当w2,b2,…,wn,bn为0时，退化为ReLU。

Maxout能够缓解梯度消失，同时又规避了ReLU神经元死亡的缺点，但增加了参数和计算量。