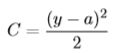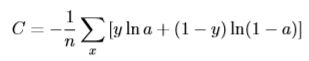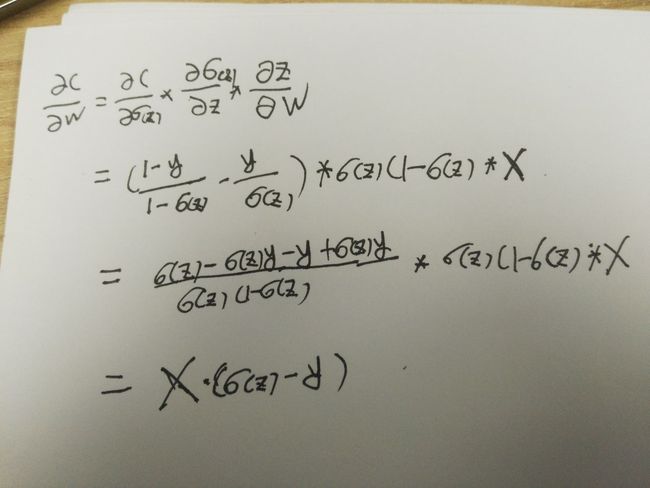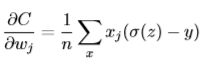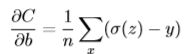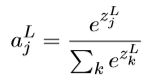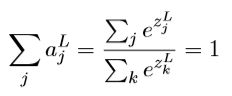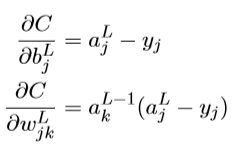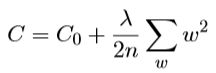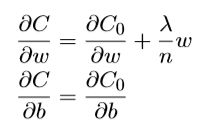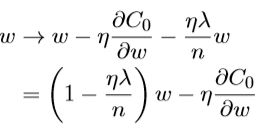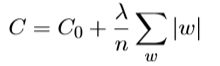神经网络的优化方式

优化问题一：训练缓慢

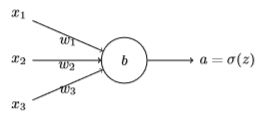
假设现在有个仅1个input节点和1个output节点的网络，x的输入为1，输出为0，要用sigmoid训练出w和b

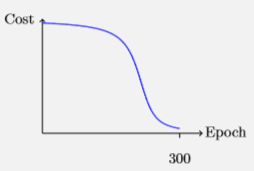
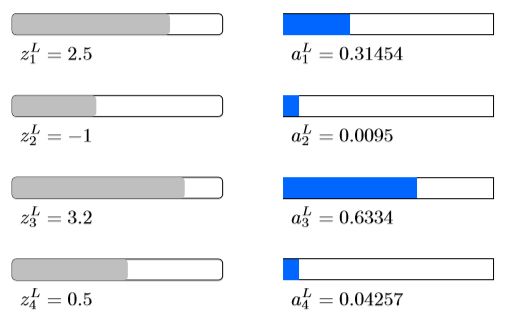
假设初始的w=2 b=2结果为0.98，离我们的训练目标0还有非常大非常大的距离，按照人类的学习经验当错误越明显时人进步的程度越大，但是我们的训练周期内结果从0.98到0表现出来的效果是这样子的：

可见在开始的100次迭代中虽然错误很明显，但是学习的成果微乎其微，这是为什么呢？

上一篇《反向传播的数学推导》我们推导过

其中

对z求导：

将x=1，y=0带入后：

前面还有篇文章《Logistic回归（1）》里也详细介绍了sigmoid函数，当z的绝对值大到某种程度后线性就趋于平滑，σ’(z)趋于0，再乘以梯度下降算法的步长参数后改变微乎其微了。

知道了原因，我们要如何解决呢？

 

 

解决方案一：交叉熵代价函数

我们把网络改造下，input拆成若干个节点，网络如下：

我们把cost function改为交叉熵（交叉熵的知识基础请参考《熵》）

PS：并不是任何一个阿猫阿狗都可以用来做costfunction，需要具备两个特性：1个是非负，1个是a≈y时函数值为0.非负很好证明了，负负得正；将a=y带入函数中，y只有0和1两个值再带入变量y中可求得第二个特性。

下面对权重w求偏导：

很容易推得对偏量b求导少乘一个x。

这样的结果已经十分优美了，很直观看得出学习的速度取决于σ(z)-y，而且不存在训练缓慢的问题！再来看下新的学习速度：

 

可以准备两种cost function的python代码了。

二次距离在深度学习数学基础—反向传播中已经出现过：

class QuadraticCost(object) :
    #平方差
    @staticmethod
    def fn(a, y):
        return 0.5*linalg.norm(a-y)**2

    @staticmethod
    def delta(z, a, y):
        return (a - y)*sigmoid_prime(z)

再添加一个交叉熵：

class CrossEntropyCost(object) :

    #计算交叉熵
    @staticmethod
    def fn(a,y):
        #nan_to_num使用0代替数组x中的nan元素
        return sum(nan_to_num(-y * log(a) - (1 - y) * log(1 - a)))

    @staticmethod
    def delta(z,a,y):
        return (a-y)

Backprop函数也需要做微调：

#反向传播主函数，最核心的部分
    def backprop(self,x,y):
        nabla_b = [zeros(b.shape) for b in self.biases]
        nabla_w = [zeros(w.shape) for w in self.weights]
        activation = x
        activations = [x]
        zs = []
        for b,w in zip(self.biases, self.weights) :
            z = dot(w,activation) +b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        #计算output层的误差律delta
        #delta = self.cost_derivative(activations[-1],y) * sigmoid_prime(zs[-1])
        delta = self.cost.delta(zs[-1],activations[-1],y)
        #修正output层
        #output对左后一层隐藏层biases的误差率是delta
        nabla_b[-1] = delta
        # output对左后一层隐藏层weights的误差率是delta多乘以一个前一层的输出
        nabla_w[-1] = dot(delta,activations[-2].transpose())
        #开始修复隐藏层，这里可以看得出方向是从后往前推
        for line in range(2, self.num_layers) :
            z = zs[-line]
            sp = sigmoid_prime(z)
            delta = dot(self.weights[-line+1].transpose(), delta) * sp
            nabla_b[-line] = delta
            nabla_w[-line] = dot(delta, activations[-line-1].transpose())
        return (nabla_b,nabla_w)

解决方案二：柔性最大值

对神经网络做改造，output层不再通过sigmoid函数来处理z，而是用“柔性最大值函数”来做处理

分母是所有分子的求和，所以有

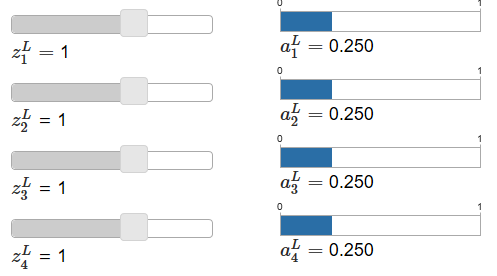
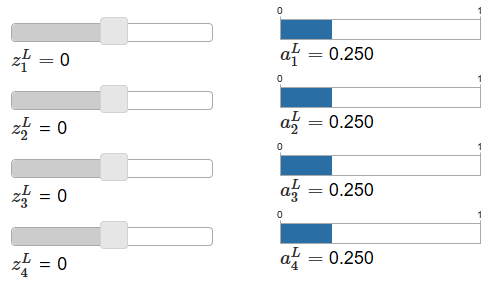
这个函数看似非常繁琐，我们可以看下这个函数的意义或者说效果是什么。在http://neuralnetworksanddeeplearning.com/chap3.html中78公式这里有动画，大家可以操作下，我也截了几张图：

特性规律是：1当其中某个z大于其它的z时，它对应的output就按照一定规则增长；2所有的output的和等于1；3当所有z相等时，output相等；4与z的绝对值大小无关

PS：如果计算概率，例如手写数字神经网络要给出各个数字结果判断的概率，明显sigmoid是做得到的，而柔性最大值可以直接代表了概率。

Output的σ(z)换成柔性最大后，costfunction也要做相应的改造换成对数似然（log-likelihood）

再来审核一下这个cost function，假如结果完美100%概率，ln1=0，cost function结果为0；如果慢慢变得不靠谱，偏差越来越大，概率从100%趋于0，-lna在不断变大。所以满足cost function的2个特性。

用C对权重和偏量求偏导：

从结果中可以看出柔性最大值+对数似然会得到与前面交叉熵类似的结果，都可以解决学习缓慢的问题。

 

 

优化问题二：过度拟合

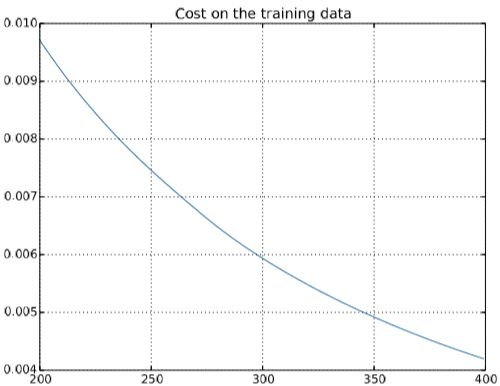
还是上面的例子，用1000幅图片来训练手写数字的神经网络，采用交叉熵作为cost fuction，训练400次迭代，可以看到cost function是平滑下降的，最后200次迭代效果如下：

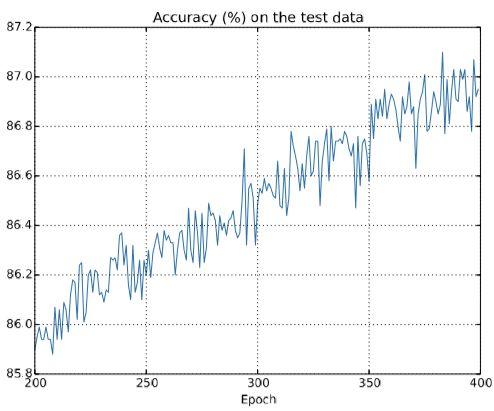
但是测试集准确率缺表现出另一种曲线：

从第280次迭代开始，准确率 82.20%左右震荡，没再有提高，所以上面cont function的下降只是一种假象，从280以后出现了过度拟合或过度训练。

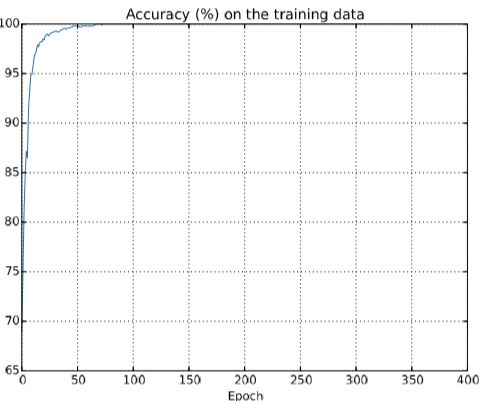
再从测试集的准确率来理解下过拟合：

可以看到从50次以后，训练集的准确率就已经达到了100%，但是应用到真正的测试集上准确率缺只有82%，说明神经网络几乎是单纯的记忆训练集，并没有很好的提取特性的信息。

 

解决方案一：增加训练集样本量

解决过度拟合有很多套路，比如可以通过观察训练集和测试集的准确率；或者将训练集中拆出一部分验证集根据一定策略提前结束迭代（Hold-out方法）；但是最有效的办法还是增加训练集的样本量，例如同样的网络我们将训练样本从1000提高到5W，效果如下图，测试准确率有了显著的提高。

事实上增加训练集样本量还可以补偿不同的机器学习算法的差距，所以数据才是王道。

 

解决方案二：规范化

最常用的规范化手段被称为权重衰减或者L2规范化，增加一个额外的项到代价函数上，这个项叫做规范化项，一般并不包含偏置b。

一般函数表达式如下：

其中C0为原始的cost function,例如交叉熵，λ>0称为规范化参数，n为训练集大小。

对w和b求偏导变为了：

偏置b的梯度下降没有变化，权重w的梯度下降变为了

这种调整被称为权重衰减。从公式中看λ越小，权重衰减越弱，反之越强。规范化的目的就是让网络偏向于学习小一点的权重。

对应的python代码改造：

#这个函数是真正做训练,eta是训练的步长
    #lmbda规范化参数
    def update_mini_batch(self, mini_batch, eta, lmbda, n):
        nabla_b = [zeros(b.shape) for b in self.biases]
        nabla_w = [zeros(w.shape) for w in self.weights]
        #训练mini_batch，mini_batch不是全部的训练集，而是分段后的一小段
        for x,y in mini_batch:
            #backpropagation  反向传播
            delta_nabla_b, delta_nabla_w = self.backprop(x,y)
            #更新临时nabla中的b和w
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b,delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w,delta_nabla_w)]
        #真正修改self中的w和b，梯度下降
        #需要注意这里w和b公式不一样
        #此处引入L2规范化
        self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w,nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb for b,nb in zip(self.biases, nabla_b)]

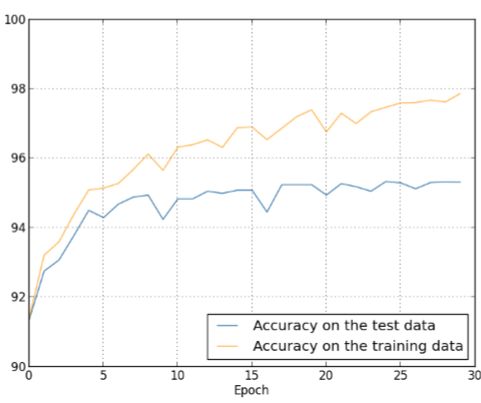
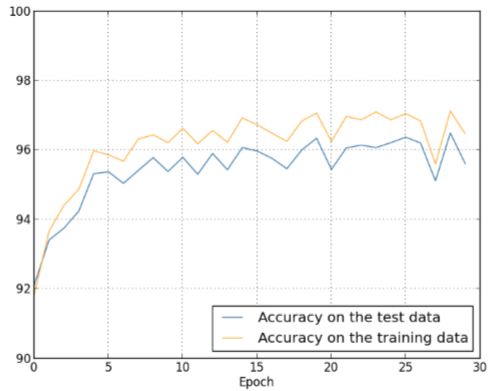
还是用前面的1000训练样本+交叉熵的cost function，得到的测试集准确率有了稳定的增长：

如果用5W个训练集，λ=5.0，只需要迭代30次：

可以看得出测试集准确率达到了96.5%，而且测试集与训练集准确率的差距明显缩小。如果进一步优化，最终可以达到98.04%的准确率。

规范化的网络往往要比非规范化的网络表现的好，这是基于实验的结论，目前并没有一套完整的关于所发生情况的解释，仅仅是一些不完备的启发式规则或者经验。通常的解释是：小的权重在某种程度上意味着更底的复杂性，也就对数据给出了一种更简单却更强大解释，因此应该优先选择。

其它规范化技术还包括：

1 L1规范化，与L2相差一个绝对值

2弃权，有点像多网络组合

3人为扩展训练数据，例如对手写数字做一定角度的偏转。

 

 

到目前为止，上面所述的基于cost function的改造提高梯度下降速率是优化了output层，目前仍然存在着隐藏层下降缓慢的问题，需要采取的手段是权重初始化。

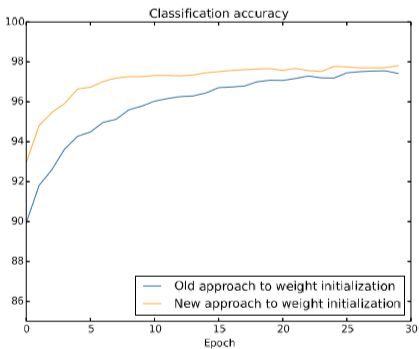
权重初始化通过给权重w除以一个（本隐藏层网络节点数开根号）使高斯函数更尖锐（测试偏置b不需要做改变），优化后神经元更不容易饱和，因此也不太可能遇到学习下降的问题。

Python代码优化后如下：

#多了一层处理，多除了一个x开根号
    def default_weight_initializer(self):
        self.biases = [random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [random.randn(y, x)/sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

改造前后效果对比图如下：

 

优化问题三：如何选择超参数

我们上面给了一些列的优化的思路，有了成熟的概念和方法论，但是目前遇到的挑战是我们怎么合理的设置λ、η等参数。

 

第一步：宽泛策略

首先要明白一点，我们的网络的参数是不可能一次性传入参数就可以建好的，它必定是一个慢慢调试的过程，而庞大的网络和训练集往往会消耗我们大量的等待时间，所以首先要做的是使问题简单化。例如手写数字识别，可以先识别0和1两个数字，这样在训练集、网络、运算消耗上都要精简很高，方面我们快速的入手和调优。

网络层次上也可以进行简化，例如[784,30,10]比起[784,100,10]训练速度上更有优势，我们可以从更小的网络开始。

训练集上也可以做一定精简，例如手写识别我们现在有5W训练集，可以用1000、500甚至100条先来进行训练，等后续找到方向后再扩大训练集个数。

宽泛策略的中心思想就是用最小的代价、最快的速度找到λ、η等参数的优化方向，不一定要准确率多高，而是要拿到肯定的、网络在优化的信号。

 

第二步：学习速率η优化

先看一个案例，不同的学习速率对cost function结果的影响

我们必须要掌握梯度下降原理再配合这张图才可以看明白图片里的信息，η=2.5时明显是步长太大了，导致一直在谷底外面不同的位置跨来跨去；η=0.25稍微好一点，但步长还是稍微大了一些，导致在谷底附近转来转去；η=0.025步长最小，可以精准的走到谷底。当然步长与训练速度是成正比的，与训练精度是成反比的，需要配合自己的经验来暂定一个η值。这里的η只需要定好数量级既可，不需要再做进一步调试，因为最终结果是所有超参数一起配合调优的，而且互相之间会动态的影响。

 

动态的学习速率能兼顾训练速度和精度的平衡，例如上图案例开始使用0.25的步长，当发现10次迭代之后没有明显效果后再减少到0.025的步长，如此迭代，每次减少一些，直到最终通过代码逻辑判断无法再优化时（步长太小或cost function不再改变）结束学习。

 

第三步：规范化参数λ优化

前面调优时先不要引入λ，参数要一个一个的调试，第三步再开始引入λ。λ的单参数优化相对简单，从λ=1.0开始尝试，然后按照10倍增加或减小，与η一样找到λ的数量级既可。

 

 

第四步：小批量数据大小选择

由于我们每次批量数据的计算是通过矩阵运算来进行的，理论上小批量数据越大训练越快（当然要在内存、cpu等硬件条件前提下），小批量数据越小拆分的小批量样本越多精准度也就越高，所以这也是个平衡的问题。

先固定一个小批量数据大小，例如100，然后进行上面第二步第三步的优化，获得η和λ的数量级，然后对η和λ组合调优，经过经验和漫长的验证拿到一对理想的参数后，再调整小批量数据大小的数量级，改数量级会影响λ的数量级，然后再进行调优。

 

选择超参数的难度很大过程就是枯燥的不断验证，我们很难找到最好的结果，但是我们可以找得到距离最好结果最近的那套参数。其本质就是效率和准确度上的平衡。

 

 

其它优化技术：

Momentum梯度下降

我们一般理解的梯度下降是基于位置的，而momentum梯度下降是基于速度的。就像我们把一个皮球滚向山谷底部，每次我们只需要决定皮球的滚动速度和方向，同时给它增加一个摩擦力作为阻力，这样只要在连续正确的方向上就会越滚越快，可以提高学习速度，同时摩擦力会逐渐的减少速度减小在谷底的震荡。

公式由：

改造为：

V就是前面所说的速度，μ是摩擦力，η是学习步长。

当μ=1时摩擦力为0，如果连续每次都在同一个方向那么v会越来越大，对w的影响也会原来越大，真正的学习步长也会越来越大；反之η=0是摩擦力直接将原始速度抵消掉，速度将无法叠加，就变成了一个普通的梯度下降，完全由cost function值来决定学习的速率。在实践中，选择合适的0-1之间的摩擦系数可以避免过量叠加速度又能提高学习速度。

 

 

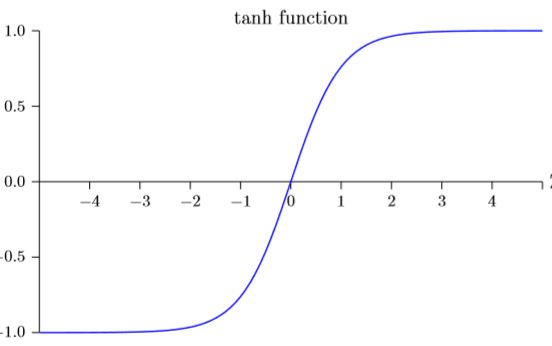
双曲正切函数tanh

曲线图如下：

形状上与sigmoid函数类似，但是tanh的范围是（-1，1），sigmoid的范围是（0，1）.Sigmoid函数与tanh函数孰优孰劣，这个目前还没有定论，只能通过不断的试验去摸索。

 

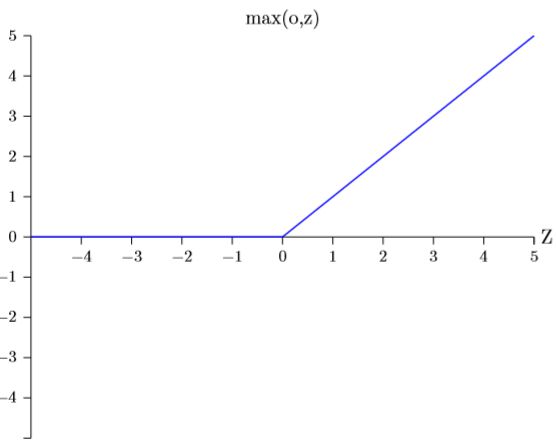
修正线性神经元ReLU（rectified linear unit）

它的输出是：

图形如下：

在sigmoid函数中结果趋于0或1时，学习速度将下降到几乎不变的程度，tanh也有类似的问题，而ReLU并不存在这个问题；而且当w*x+b为负数时，梯度就消失了，神经元就完全停止了学习，提前终止。

更新：

重点再介绍下弃权（Dropout）

每次在训练时临时删除一部分隐藏层神经元，同时让输入层和输出层神经元保持不变，如下图：

一次前向传播和BP后，先恢复所有隐藏层神经元，再随机删除部分隐藏层神经元，如此迭代，直到训练结束。

这么做的意义是什么？答案是消除过度拟合。

随机的删除神经元相当于基于相同的输入输出我们使用了不同的网络在训练，最终的训练结果相当于所有网络“投票”决定的。虽然不同的网络可能会以不同的方式过度拟合，平均法可以帮助我们消除一部分过度拟合。

机器学习中也有类似的“强学习器”和“弱学习器”，详见《分类器集成和非均衡分类》，原理上同出一辙。