【HDL系列】Brent-Kung树形加法器原理与设计
目录
一、并行加法器基本方法
二、进位链计算重构原理
三、Brent-Kung加法器
四、Verilog设计
在超前进位加法器中，其进位可以并行计算出，打破了进位链传播中当前的进位依赖于前一级的进位的关系，使得第n位进位只与输入有关。
但是，对于大位宽加法器，其每一个进位生成的逻辑面积耗费大，芯片造价成本上升，在前几期中已有介绍。很多研究者致力于在时间延迟与逻辑门数之间寻找平衡点，却极少数关注如何使用简洁与规则的方式最小化芯片面积和设计成本。本文将介绍的Brent-Kung加法器，由Richard P.Brent和H.T.Kung教授于上世纪80年代提出，Brent-Kung加法器是一种树形加法器，采用了树形结构，达到了N比特加法器延迟正比于log N, 面积正比于N的效果。本文介绍并行加法器基本方法，Brent-Kung加法器基本原理与Verilog设计。
一、并行加法器基本方法
对于N比特的A和B两数，结果为N比特S和1比特进位Cout，超前进位加法器的进位链与和公式的计算公式如下（为了统一，此处序号从1开始到N）：
其中：
如对于C4的生成，其算式如下：
每个进位的生成依赖于G和P，对于每一位进位，如何做到更加节省逻辑面积与减少计算时间呢？正是利用了一种树形结构，通过以下基本方法生成进位与和达到。
图中输入为N比特A和B，输出N比特S和1比特Cn即Cout，已用红色标出。这种并行加法器的基本方法即将输入数A和B通过一部分逻辑转化为G和P，P由A和B异或，G由AB相与即可，其中的G和P通过树形门级结构用于生成进位Cn与和Sn。
二、进位链计算重构原理
Brent-Kung加法器定义了以下运算“o”:
其中的p,g,g’,p’均是二进制数。
上式这么看容易糊涂，运算“o”想表达的意思是以下两个式子：
（1）输入p,g,g’,p’，输出g+p.g’
（2）输入p,g,g’,p’，输出p.p’
特别提醒：此部分的实质为对超前进位加法器的进位链计算进行了重构，如果对超前进位加法器的进位计算熟稔于心，可忽略以下定理，并只要记住定理后（Gi，Pi）的生成式子。
定理一、
Ci = Gi, i=1,2,…N
因为C0=0,所以C1 = G1 + P1*C0 = G1
为什么Ci=Gi，此处证明忽略，可以从假定Ci-1=Gi-1开始。
定理二、
同时，
基于以上两式子可以看出，“o”操作符合交换律，(gi,pi)操作可以使用任意顺序。根据以上定理一和定理二可以得出，此式子将用于树形进位链生成：
三、Brent-Kung加法器
由以上方法可知，pi由AB异或生成，gi由AB相与生成。
而新的进位由下式生成，即Ci=Gi，只要计算出以下式子就可以得到所有的进位Gi即可。
如何计算呢？
先看一个例子，当n=8时，（G8,P8）的计算方法如下图。
(G8，P8)的树结构计算方法
其中白色圈表示数据传递，数据前后没有变化；黑色圈表示上文中定义的“o”操作，其计算示意图如下。
白色圈与黑色圈操作计算方法示意
在T=3时刻G8和P8的计算如下：
（G8，P8）= （g8，p8）o（g7，p7）o（g6，p6）o（g5，p5）o（g4，p4）o（g3，p3）o（g2，p2）o（g1，p1）
对于一般问题（Gi,Pi），i=1,2,3，…N的计算，其结构图如下：
16比特Brent-Kung加法器进位计算图，图片来源Brent-Kung论文
如其中C9=G9，（G9，P9）=（G8,P8）o（g9,p9）,所以在生成C9前还进行了一次“o”操作。
从逻辑层数，扇入扇出和布线拥塞度三个方面看该树形加法器，Brent-Kung加法器的拓扑结构经历逻辑层数较多，需要(2logN – 1)级，扇入扇出和布线拥塞度较低。
四、Verilog设计
设计一个N比特的Brent-Kung加法器，重点在于从门级去展开各路进位的生成逻辑，生成该进位链的树形结构。
以下是16比特的Brent-Kung加法器，分三部分：
（1）生成p，g信号，由半加器模块组成；
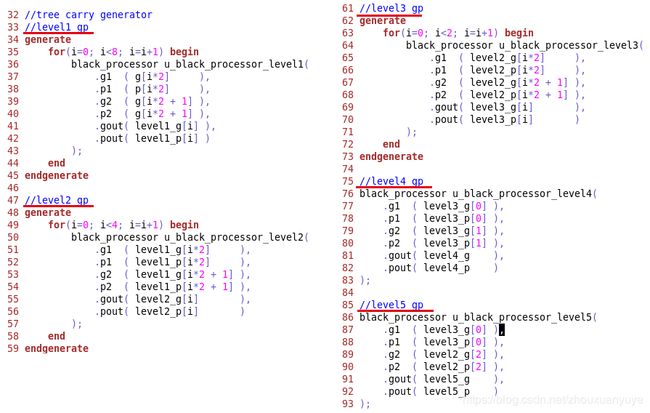
（2）“o”操作单元实现，由p，g信号生成进位链逻辑，一部分可规律性地通过verilog generate语句生成，其余部分通过模块化或者assign单独实现；
（3）生成输出进位Cout和S信号。
注：如果不假定C0=0，则可以将（gc,pc）=（C0,0）参与到（G1，P1）的计算中去。
16比特Brent-Kung加法器PG生成逻辑
16比特Brent-Kung加法器7级进位生成逻辑——第1-5级
16比特Brent-Kung加法器7级进位生成逻辑——第6级
16比特Brent-Kung加法器7级进位生成逻辑——第7级
16比特Brent-Kung加法器和S生成逻辑
欢迎批评指正，更多阅读，关注“纸上谈芯”，不定期更新，共同学习:
