基于深度学习的人脸识别算法

简介

我们经常能从电影中看到各种神奇的人脸识别技术，例如图1。人脸识别技术是基于面部特征信息进行身份识别的一种生物识别技术。该技术在图片/视频中，从人脸的角度入手，识别出画面中的人物是谁。如图2所示，严格来讲，这个过程包括人脸检测 (face detection) ，人脸对齐(face alignment) ，人脸识别 (face recognition) 三个部分。人脸检测目的是从图片/视频中，找到人脸，并确定人脸的位置； 人脸对齐目的是找到人的面部特征点（鼻子，眼睛，嘴巴等），解决人脸的角度变化问题；人脸识别目的是识别人脸，确定身份。本文我们只关注人脸识别这部分工作。

人脸识别是一个历史悠久的任务，从20世纪50年代开始，研究人员已经开始关注人脸识别这个领域。从最早基于人脸几何结构特征，到基于建模方法，局部特征描述子(Gabor, LBP)，目前主流的方法是基于深度学习的方法。自从2012年，AlexNet [1] 以巨大领先优势获得ImageNet第一名以后，研究人员来开始思考是否能够用深度学习方法来做人脸识别的任务。高性能计算机 (CPU, GPU) 出现，大规模人脸数据集出现 (LFW [2] ，CISIA-WebFace [3] ， MS-Celeb-1M [4]) ，加上对人脸识别问题的深刻理解，基于深度学习的人脸识别算法将人脸识别精度提高了一个新的台阶。损失函数是CNN (卷积神经网络) 重要组成部分，它指导了网络的优化目标。本文从损失函数入手，简单介绍基于CNN的人脸识别的损失函数的原理以及发展过程。
在人脸识别中，每个人都可以看做一类，直观的想法可以用分类算法来做。但是，不同于分类算法，人脸数据集一般个人（类别）较多，每个人的样本却不多，并且样本不能覆盖所有人，测试的时候很多情况会出现训练集中不存在的样本。基于此，通用的方法把人脸识别看做一个距离度量的问题，通过学习样本的特征，然后计算样本之间的距离，来确定人物身份。本文主要介绍以下四种常用的损失函数：Contrastive Loss[5]，Triplet Loss [6]， Center loss [7]和 A-Softmax loss [8]。

Contrastive Loss

早在2005年，Chopra[5]就提出了Contrastive loss就用来解决人脸验证/识别问题。首先，作者从人脸数据集，选出若干对人脸，构成人脸二元组。这样的人脸二元组包括两种情况：属于同一个人；属于不同的人，见图3。如果一个人脸对属于同一个人，标记这种人脸对的标签Y=0，如果一对人脸中，属于不同的人，那么标记这种人脸对的标签Y=1。这样做还有一个好处，能够扩充数据集，支持CNN的训练。以论文中的AT&T Database of Faces [9] 为例，一共400张图片，40个人，每个人10张图片。同一个人的人脸二元组有4000个，不同人的人脸二元组有156000个，一定程度上更满足CNN大规模训练数据要求。

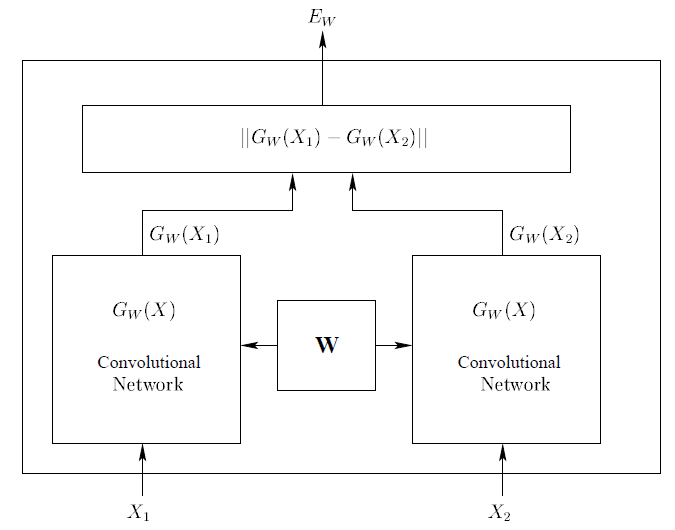
为了方便阐述，我把论文中的网络结构也放到这里，如图4所示：

Contrastive loss 定义如下：
$$l(W)=\sum _{i=1}^{P}L(W,(Y,X_1,X_2{)}^i)$$

$$L(W,(Y,X_1,X_2{)}^i)=(1-Y)L_G(E_W(X_1,X_2{)}^i)+Y{L}_I(E_W(X_1,X_2{)}^i)$$

这里W表示网络的参数，$(Y,X_1,X_2)$ 表示第i个人脸二元组， $L_G$表示属于同一类的部分损失函数， $L_I$表示属于不同人脸的损失函数， P是训练的人脸二元组的数目。$L_G$这里 是一个单调递增的函数， $L_I$是一个单调递减的函数。一个最简单的例子$L_G(x)=x,L_I(x)=-x$ , 那么上述损失函数L变为：
$$L(W,(Y,X_1,X_2{)}^i)=(1-Y)E_W(X_1,X_2{)}^i-Y(E_W(X_1,X_2{)}^i))$$

如果Y = 0，表示输入的是属于同一个人的人脸二元组，后面一项为0，最小化损失函数L让$E_W(X_1,X_2)$最 小，既是类内的距离尽可能小。当Y = 1时，表示输入的人脸二元组属于不同的人，前面的一项为0，最小化损失函数L，等价于$E_W(X_1,X_2)$变大，既是类间的距离尽可能大。以上过程就是contrastive loss 函数。

Triplet Loss

FaceNet [6] 文中提出了Triplet Loss，与Contrastive loss的输入二元组不同的是，Triplet输入时人脸三元组。随机从某个人照片中选择一张，叫做Anchor；再从这个人照片中选择另一个照片，叫做Positive；最后随机选择一张其他人的照片，叫做Negative， 这样就构成了图像的三元组。图5就是三元组的一个例子。

人脸识别的优化目标是同一个人距离尽可能近，不同人的距离尽可能远。假设$X_i^a,X_i^p,X_i^n$ 分别代表第i个三元组的Anchor，正例，负例。 $f(X_i^a),f(X_i^p),f(X_i^n)$分别代表对应的特征。Triplet Loss损失函数如下所示：
$$L=\sum _i^N[\Vert f(x_i^a)-f(x_i^p){\Vert }_2^2-\Vert f(x_i^a)-f(x_i^n){\Vert }_2^2+\alpha {]}_{+}$$

表示[]内的值如果大于零的时候，损失等于该值，小于零的时候，损失等于0。 $\alpha$ 是超参数，表示Anchor和Positive特征距离应该比Anchor和Negative的特征距离大于 。最小化上述损失函数，就能保证同一个人脸特征距离小于不同人的人脸特征距离了。

Center Loss

二元组正例和负例存在严重不平衡，选择什么的负例呢？三元组选择有多种多种，但什么样的三元组是最优的选择？ 引入了二元组，三元组为了解决问题，然而又带来了新的问题。有木有什么方法可以不必纠结如何选择有效的二元组，三元组吗？当然有的。直观的想法就是用Softmax 作为损失函数训练分类的损失，用全连接层特征作为人脸特征进行相似度比较。但是，Softmax只会使类别分开，并不会约束类内距离，特征会相对稀疏散布在分界面之间，我自己做了一个实验，用Softmax训练了Mnist数据集， 设置最后一层全连接层特征为2维，可视化出现结果如图6所示。

由于Softmax损失不会对类内特征做任何约束，那么在特征空间（以特征维度为2示例）中，分界面之间的区域都会被认为是一类。在人脸识别任务下，人脸数据集很难覆盖所有人，也就说如果把单个人为一类的话，分界面之间区域特征都认为这个人是很不合理的。就会出现新的类别测试的时候，特征会落到某个类特征区域内，那么就会判断为该类，出现误判。针对这种情况，Wen [8]提出了center loss。整个训练的损失函数等于Softmax loss加上center loss。
其中center loss损失函数如下：
$$L_C=\frac{1}{2}\sum _{i=1}^m(\Vert x_i-c_{y_i}\Vert {)}_2^2$$

$C_{yi}\in R^d$表示第$Y_i$ 类的特征中心。Center loss目标是让每类的特征尽可能集中，让每类在特征空间内所占的范围尽可能小，测试时当新的类别出现时，不会误判为已有的类别。结合center loss和softmax loss在一起，在Mnist的结果如图6右图所示，每类所占的空间极小。新的类出现，减少了误判的可能。

A-Softmax Loss

从图6左图可以看出，使用Softmax作为分类器，在二维空间内特征分布呈现圆形，三维空间中分布呈现球形。因此，在圆形、球形的分布中，如果使用欧式距离来衡量特征之间的距离，是不合理的，基于此，作者提出了用角度距离来衡量特征之间的距离的方法A-Softmax。以二分类为例，传统的Softmax 分类器可以得到分界面：
$$W_1^{T}x+b=X_2^{T}x+b\to (W_1^T-W_2^T)x-(b_1-b_2)=0$$
可以把Softmax 写成角度的形式:
$$||W_1||||x||cos({\theta }_1)+b_1=||W_2||||x||cos({\theta }_2)+b_2$$
将W, b进行normalize 操作以后使$||w_i||=1,b_i=0$ ，分界面就变为了 $||x||(cos({\theta }_1)-cos({\theta }_2))=0$，这样就可以从角度入手学习分界面，作者将这种方法叫做Modified Softmax。在人脸任务中，还需要保证同一个人的特征尽可能近，不同的人特征尽可能远。作者在Modified Softmax基础上提出了加入超参数m来限制类内距离小于类间距离。在Modified Softmax中，如果$cos({\theta }_1)>cos({\theta }_2)$ 认为输入第一类，修改的A-Softmax 则是$cos(m{\theta }_1)>cos({\theta }_2)$成立的时候，才被认为是第一类，满足这样条件的θ_1 范围就降低了很多，这样就缩小了类内的距离。论文中m=4。第二类同理。
修改后的A-Softmax损失函数如下所示：
$$L_i=\frac{1}{N}\sum _i-\log (\frac{e^{\Vert x_i\Vert \cos (m{\theta }_{(}{y}_i),i)}}{e^{\Vert xi\Vert \cos (m\theta yi,i)}+{\sum }_{j̸=yi}{e}^{\Vert xi\Vert \cos (\theta j,i)}})$$

Softmax，Modified Softmax， A-Softmax作用下的特征分布如图7所示：

Cosine 距离是一个非线性距离，在人脸度量上比线性的欧式距离更有优势，加入超参数m，相当于在原有角度距离的基础上，限制了类内距离，保证类间距离大的同时类内距离小。正是如此，该算法也取得了Megaface竞赛的第一名。

结语：由于本人水平有限，文中如有错误，请留言指出错误，万分感谢。

参考文献：

[1] Alex Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton ImageNet Classification with Deep Convolutional Neural Networks NIPS 2012
[2] http://vis-www.cs.umass.edu/lfw/
[3] http://www.cbsr.ia.ac.cn/english/CASIA-WebFace-Database.html
[4] https://www.microsoft.com/en-us/research/project/ms-celeb-1m-challenge-recognizing-one-million-celebrities-real-world/
[5] Sumit Chopra, Raia Hadsell, Yann LeCun Learning a Similarity Metric Discriminatively, with Application to Face Verification. CVPR 2005
[6] Florian Schroff, Dmitry Kalenichenko , James Philbin. FaceNet: A Unified Embedding for Face Recognition and Clustering CVPR 2015
[7] Yandong Wen, Kaipeng Zhang, Zhifeng Li, Yu Qiao. A Discriminative Feature Learning Approach
for Deep Face Recognition ECCV 2016
[8] Weiyang Liu, Yandong Wen, Zhiding Yu, Ming Li, Bhiksha Raj, Le Song SphereFace: Deep Hypersphere Embedding for Face Recognition CVPR 2017