纪中暑假集训 2020.07.24【NOIP提高组】模拟 反思+题解

这次题目相对来说比较简单，可是我也只拿了130分，本来有220的，T1一个2bytes的小细节的错误让我没了90分，要总结经验！

T1：【NOIP2015模拟10.28B组】序章-弗兰德的秘密

Description

背景介绍（有意思……）
弗兰德，我不知道这个地方对我意味着什么。这里是一切开始的地方。3年前，还是个什么都没见过的少年，来到弗兰德的树下，走进了封闭的密室，扭动的封尘已久机关，在石板上知道了这个世界最角落的最阴暗的东西。那种事情，从未忘怀，从未动摇，我还记得，那一天，我，里修，第一次拔起了剑……

弗兰德的密室里，机关上方画着两棵树的字样，机关下方是一个有数字的刻度……
弗兰德最高的两棵树，只要知道两棵树的共同的相似度就行了……
给定两棵有根树，可以任意删除两棵树上的节点（删除一棵节点必须保证该节点的子树内的所有节点也必须要被删除，换一种说法，删除后的树必须联通并形成一棵树，且根节点不能被删除），使得删除后的两棵树同构，这两棵树有一个共同大小，即树的size，最大化同构的树的size即为机关的答案……

注：两棵同构的树要满足以下条件：
1、两棵树节点个数相等。
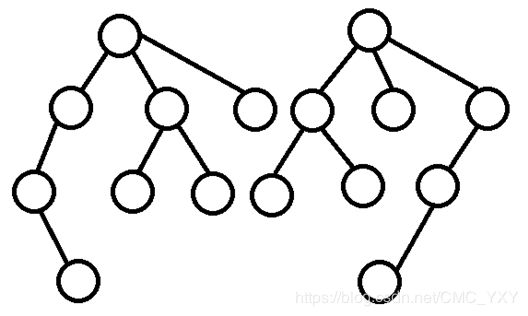
2、两棵树的以根节点的儿子为根子树对应同构。如下图，为两棵同构的有根树。
如下图，为两棵同构的有根树。

Input

一行两个整数n,m分别表示两棵有根树的大小。
以下n-1行描述第一棵树，每行两个数x,y表示x号节点是y号节点父亲。
以下m-1行描述第二棵树，每行两个数x,y表示x号节点是y号节点父亲。
数据保证两棵树的1号节点均为根。

Output

一行一个数，表示两棵树的相似度（删除后最大化的同构树的大小）。

Sample Input

3 3
1 2
1 3
1 2
2 3

Sample Output

2

【样例解释】

第一棵树可以保留1号节点和2号节点删除3号节点，也可以保留1号节点与3号节点删除2号节点，
第二棵树保留1号节点和2号节点删除3号节点。
剩下的树同构，树的节点个数均为2。

Data Constraint

对于30%的数据，1 ≤ n ≤10
对于60%的数据，1 ≤ n ≤ 100
对于100%的数据，1 ≤ n ≤ 1000数据保证两棵树上每个节点的度均不超过5。

反思&题解

比赛&正解思路： 很显然是树形DP，看到节点度数不超过5，果断抛弃链式前向星，邻接表直接干，我们用两个dfs，一个用来遍历第一棵树的节点，一个用用来转移，设$f[i][j]$为第一棵树的第i个节点与第二棵树的第j个节点的最大同构，那么这道题就很好做了，因为是用dfs转移，所以没有固定的方程，比较好做，具体大家可以自己思考一下，综合code理解
反思： 细节一定要注意好了！

CODE

#include
using namespace std;
int n,m,f[1005][1005],tree1[1005][1005],tree2[1005][1005],num1[1005],num2[1005],k1,k2;
bool bz[1005];
void dp(int k,int tot,int k1,int k2)
{
	if (k>num1[k1])	f[k1][k2]=max(f[k1][k2],tot);
	else
	{
		dp(k+1,tot,k1,k2);
		int i;
		bool flag=true;
		for (i=1;i<=num2[k2];i++)
		{
			if (!bz[i])
			{
				bz[i]=true;
				flag=false;
				dp(k+1,tot+f[tree1[k1][k]][tree2[k2][i]],k1,k2);
				bz[i]=false;
			}
		}
		if (flag) f[k1][k2]=max(f[k1][k2],tot);
	}
}
void dg(int now)
{
	if (!num1[now])
	{
		int i;
		for (i=1;i<=m;i++)
			f[now][i]=1;
	}
	else
	{
		int i;
		for (i=1;i<=num1[now];i++)
			dg(tree1[now][i]);
		for (i=1;i<=m;i++)
		{
			if (!num2[i]) f[now][i]=1;
			else
			{
				dp(1,0,now,i);
				f[now][i]++;
			}	
		}	
	}
}
int main()
{
	freopen("frand.in","r",stdin); 
	freopen("frand.out","w",stdout);
	scanf("%d%d",&n,&m);
	int i;
	for (i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		tree1[x][++num1[x]]=y;
	}
	for (i=1;i<m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		tree2[x][++num2[x]]=y;
	}
	dg(1);
	printf("%d\n",f[1][1]);
	return 0;
}

T2：【NOIP2015模拟10.28B组】圣章-精灵使的魔法语

Description

【背景介绍】（搞笑……）
“魔法？？？算了吧，这种东西我肯定学不了的啦！”明明是个剑士，却被眼前这位洋洋自得的精灵使——弗洛莉拖出去学魔法，真是个没事找茬的家伙……
“没事啦。作为一名冒险者会发生很多情况，中毒啦，受伤啦，被咒语束缚之类的，没有魔法就很难办的呀！”她到是好像一副什么都懂的样子，真是令人火大。
“都说我是个人类了，魔法这种东西学起来很困难的吧！”我只好找个看似靠谱的借口。
然而，她那不屈不挠的声音又响了起来：“人类虽然与自然的共鸣，也就是魔法的连接较少，但如果认真训练的话还是可以做到的呢！总之，试试看吧！念念咒语之类的！”弗洛莉把魔法书一把拍在了我面前。
我没兴趣地瞟了一眼，“哼。这种东西我不看也会，伦福萨——密西卡！”才刚刚念完不知道从哪里偷学来的魔法咒语。随即，便听到弗洛莉的一声尖叫，使得整个酒店的人的视线都往这边看来。喂喂喂，别往我这边看啊，我有视线恐惧症啊！！！！况且，我只是把她正在吃的面包的样子变成虫子而已，谁会料到这种情况啊啊啊！！
“真是的，弗洛莉才是老拖我的后腿呢！”我没好气地笑道……
“里修！你……”她从牙缝里挤出了一个字。我顿感不妙，见到了那张比魔鬼还可怕的扭曲的面孔。“真是个魔法的天才哪！”她一扫之前不愉快的表情，想我露出大拇指，好像是在夸奖我的样子。
咦？她竟然没有打我，那真是我福大命大。我这样想着，便一屁股坐在了凳子上，松了口气……
【题目描述】
“伦福萨”【即" ( “】和“密西卡”【即” ) “】是两种不同的精灵咒语，已知一个成功的咒语符合如下的规定：
每一个密西卡之前都可以对应匹配到一个伦福萨，即为一个合法的精灵魔法咒语。
方便的是，我们将“伦福萨”视为” ( “，“密西卡”视为” ) “，合法的精灵魔法咒语即为一个合法的括号序列。
如：” ( ( ( ) ) ) “” ( ( ) ( ) ) “” ( ) ( ) ( ) “均为合法的魔法咒语，” ) ( “” ( ) ) ( “” ( ( “均为不合法的魔法咒语。
现在弗洛莉给我一个长长的“伦福萨”【即” ( “】和“密西卡”【即” ) “】的片段，每次给我一个l和r，让我判断需要在这个片段前最少添多少个“伦福萨”【即” ( “】，以及最少添多少个“密西卡”【即” ) “】可以成为一个合法的魔法咒语，更令人不爽的是，弗洛莉有的时候还会把一个“伦福萨”【即” ( “】变成“密西卡”【即” ) “】，或把一个“密西卡”【即” ) “】变为“伦福萨”【即” ( "】。
题目一大堆都是废话……

Input

第一行两个正整数n,m，表示我现在含有的咒语元素（“伦福萨”【即" ( “】和“密西卡”【即” ) “】）的个数以及弗洛莉给我的任务个数，
第二行包含n个字符（“伦福萨”【即” ( “】或“密西卡”【即” ) “】）表示一开始弗洛莉给我的咒语片段。
以下m行包括两种任务：
Change x，表示弗洛莉将位置为x上的咒语片段进行一次变换（原来是“伦福萨”【即” ( “】变为“密西卡”【即” ) “】，原来是“密西卡”【即” ) “】变为“伦福萨”【即” ( “】）。
Query l r，询问从l到r的区间的片段，在这个片段前最少添上多少个伦福萨”【即” ( “】，在这个片段后最少添上多少个“密西卡”【即” ) "】可以成为合法的魔法序列。

Output

每个询问对应一行答案，每行包括两个整数，表示在这个片段前最少添上多少个伦福萨”【即" ( “】，在这个片段后最少添上多少个“密西卡”【即” ) "】可以成为合法的魔法序列。

Sample Input

6 4
(()()(
Query 1 3
Query 3 6
Change 6
Query 1 6

Sample Output

0 1
1 1
0 0

【样例解释】

1.片段为“ ( ( ) ”最右边填1个 ) 即可。
2.片段为“ ) ( ) ( ”最左边添1个 ( 最右边添1个 ) 即可。
3.片段为“ ( ( ) ( ) ) ”已经是合法片段。不需添加。

Data Constraint

对于20%的数据，1 ≤ n,m ≤ 100
对于40%的数据，1 ≤ n,m ≤ 3000
另外含有30%的数据，数据中不包含修改操作。
对于100%的数据，1 ≤ n,m ≤ 150,000

反思&题解

比赛思路： 一眼线段树，第二眼……怎么处理这个括号序列啊……主要是我线段树基础没那么好，所以无奈只能暴力骗分
正解思路： 只需要记录区间内有需要添加左括号和右括号，change的时候将叶子节点取反（0变1,1变0）就行了，连懒标记都不用打（我太弱了……）
反思： 线段树要随时温习，这是一个很重要的知识点

CODE

#include
using namespace std;
int tree[600005][2],n,m,ans1,ans2;
char cz[7],s[150005];
void build(int now,int l,int r)
{
	if (l==r)
	{
		if (s[l-1]=='(') tree[now][1]=1;
		else tree[now][0]=1;
	}
	else
	{
		int mid=l+r>>1;
		build(now<<1,l,mid);
		build(now<<1|1,mid+1,r);
		tree[now][0]=tree[now<<1][0]+max(0,tree[now<<1|1][0]-tree[now<<1][1]);
		tree[now][1]=tree[now<<1|1][1]+max(0,tree[now<<1][1]-tree[now<<1|1][0]);
	}
}
void find(int now,int l,int r,int x,int y)
{
	if (l==x && r==y)
	{
		ans1=tree[now][0];
		ans2=tree[now][1];
	}
	else
	{
		if (l!=r)
		{
			int mid=l+r>>1;
			if (y<=mid) find(now<<1,l,mid,x,y);
			else if (x>mid) find(now<<1|1,mid+1,r,x,y);
			else
			{
				find(now<<1,l,mid,x,mid);
				int tot1=ans1,tot2=ans2;
				find(now<<1|1,mid+1,r,mid+1,y);
				int tot11=ans1,tot22=ans2;
				ans1=tot1+max(0,tot11-tot2);
				ans2=tot22+max(0,tot2-tot11);
			}
		}
	}
}
void change(int now,int l,int r,int v)
{
	if (l==v && r==v)
	{
		tree[now][0]^=1;
		tree[now][1]^=1;
	}
	else
	{
		if (l!=r)
		{
			int mid=l+r>>1;
			if (v<=mid) change(now<<1,l,mid,v);
			else change(now<<1|1,mid+1,r,v);
			tree[now][0]=tree[now<<1][0]+max(0,tree[now<<1|1][0]-tree[now<<1][1]);
			tree[now][1]=tree[now<<1|1][1]+max(0,tree[now<<1][1]-tree[now<<1|1][0]);
		}
	}
}
int main()
{
	freopen("elf.in","r",stdin);
	freopen("elf.out","w",stdout);
	scanf("%d%d",&n,&m);
	scanf("%s",s);
	build(1,1,n);
	int i;
	for (i=1;i<=m;i++)
	{
		scanf("%s",cz);
		if (cz[0]=='Q')
		{
			ans1=0;
			ans2=0;
			int ll,rr;
			scanf("%d%d",&ll,&rr);
			find(1,1,n,ll,rr);
			printf("%d %d\n",ans1,ans2);
		}
		else
		{
			int xx;
			scanf("%d",&xx);
			change(1,1,n,xx);	
		}	
	}
	return 0;
}

T3：【NOIP2015模拟10.28B组】终章-剑之魂

Description

【背景介绍】（中二……）
古堡，暗鸦，斜阳，和深渊……
等了三年，我独自一人，终于来到了这里……
“终焉的试炼吗？就在这里吗？”我自言自语道。
“终焉的试炼啊！就在这里啊！”我再一次自言自语道。
“这背后可能有那个东西吗？”我自言自语道。
“这背后一定有那个东西呢！”我又一次自言自语道。
我沉默着，踏上黑漆漆的索桥，小心翼翼地，拿出锋利的注入我灵魂的双剑……
“那么，我们开始吧……”我最后一次自言自语道。
【题目描述】
My soul of my sowrd!
终焉的试炼即将到来，作为一名有修养的剑士，虽然没有习得n刀流但是二刀流还是没问题的。然而我也是个剑的收藏者，家里屯着n把剑，每一把剑都有一个灵魂值a[i]，由于一些剑之间可能有共鸣，所以我需要两把契合度最高的剑。据剑圣所说，两把编号为i,j剑的契合度为a[i] and a[j]。如何深得剑的灵魂呢？
注：AND 为按位与运算，先将数转成二进制，不满位数的补全0，然后成为两个长度相同的二进制数，处理的时候，两个相应的二进制位都为1，该位的结果值才为1，否则为0。例下图。

Input

第一行一个整数n，代表藏剑数。
第二行n个整数，第i个整数表示a[i]。

Output

输出包含一个正整数，最好的两把剑的契合度。

Sample Input

5
12 5 6 3 1

Sample Output

4

【样例解释】

5 and 6=4或者12 and 5=4或者12 and 6=4

Data Constraint

对于40%的数据 n ≤ 1,000
对于100%的数据 n ≤ 1,000,000，0 ≤ a[i] < 2^31

反思&题解

比赛&正解思路： 第一眼以为是DP，但是$O($$n$ $log$ $n$)我觉得咋也不可能，之后看到数据范围豁然开朗，$2^{31}$很明显有玄机，我们就转化为二进制一位一位枚举，从高位开始（因为从高位取最优），之后我们判断一个$a[i]$如果前$i-1$位与答案相同且第i位是1则是合法的，只要有两个以上合法的即更新答案
反思： 数据如果是2的多少次方的话那么可以往位运算想
PS： 大家敢信这题的数据水到排序之后两两and都能过……

CODE

#include
using namespace std;
long long a[1000005],n,ans;
int main()
{
	freopen("sword.in","r",stdin);
	freopen("sword.out","w",stdout); 
	scanf("%lld",&n);
	long long i;
	for (i=1;i<=n;i++)
		scanf("%lld",&a[i]);
	for (i=31;i>=1;i--)
	{
		long long j,tot=0;
		for (j=1;j<=n;j++)
		{
			if ((ans&a[j])==ans)
			{
				if ((a[j]&(1<<i-1))) tot++;
			}
		}
		if (tot>=2) ans+=(1<<i-1);
	}
	printf("%lld\n",ans);
	return 0;
}