信号与系统——离散系统分析的MATLAB实现

一、实验目的
1．掌握利用MATLAB进行离散系统的时域分析、z域分析和频域分析的基本方法；
2．掌握根据系统函数的零、极点设计滤波器的方法；
3．深刻理解离散时间系统的系统函数在分析离散系统的时域特性和频率特性中的重要作用及意义。

二、实验内容
1、已知系统y(k)-y(k-1)-2y(k-2)=f(k)，输入f(k)=(-1)^k ε(k)，起始状态为y(-1)=0, y(-2)=1/6。
（1）利用MATLAB进行时域分析，求单位序列响应、零输入响应、零状态响应和全响应，2018aMATLAB程序如下：

clear
clc
a=[1,-1,-2];b=[1,0,0];
n=0:10;
f=(-1).^n;                %输入信号，长度为11
qz=[0,1/6];               %起始状态
ct=filtic(b,a,qz);        %初始条件
h=impz(b,a,n)             %求单位序列响应
yzi=filter(b,a,0*f,ct)    %求零输入响应，ct为系统初始条件
yzs=filter(b,a,f)         %求零状态响应
y=yzi+yzs                 %求全响应 
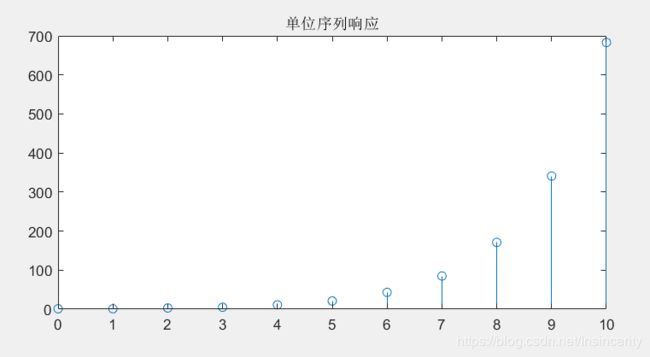
subplot(2,2,1);stem(n,h);title('单位序列响应');
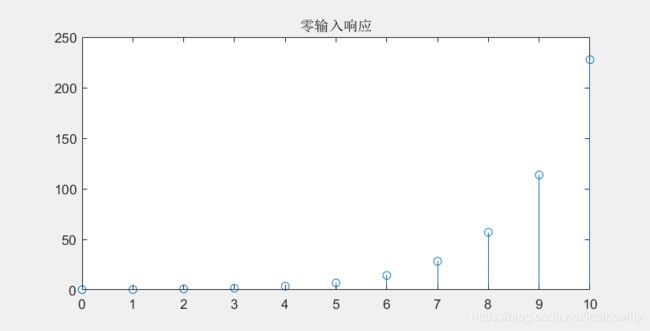
subplot(2,2,2);stem(n,yzi);title('零输入响应');
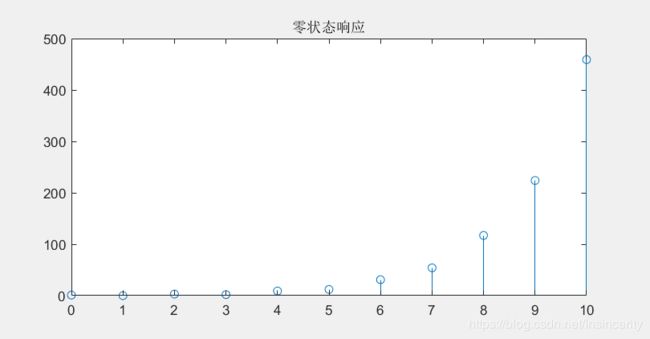
subplot(2,2,3);stem(n,yzs);title('零状态响应');
subplot(2,2,4);stem(n,y);title('全响应');

运行结果：
单位序列响应
零输入响应

零状态响应

全响应

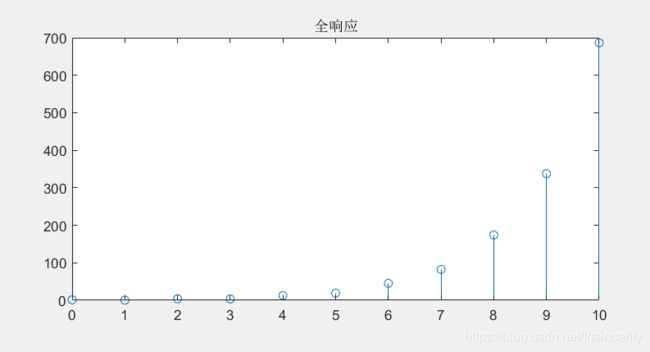
（2）利用MATLAB进行z域分析，求零输入响应、零状态响应和全响应，2018aMATLAB程序如下：

clear
clc
syms z real
a=[1,-1,-2];b=[1,0,0];             %系统模型
qz=[0,1/6];                        %起始状态
f=str2sym('(-1)^k*heaviside(k)');  %输入信号
F=ztrans(f);                       %输入信号的z变换
Zn=[z^2,z,1];
A=a*Zn';B=b*Zn';                   %构建A和B
C=-[a(3)*z+a(2)*z^2,a(3)*z^2]*qz'; %构建C
H=B/A;                             %构建系统函数
Yzi=C/A;
yzi=iztrans(Yzi)
Yzs=H.*F;
yzs=iztrans(Yzs)
y=yzi+yzs

运行结果：
零输入响应 yzi = (-1)^n/9 + (22^n)/9
零状态响应 yzs = (13(-1)^n)/18 + 2^n/9 + ((-1)^n*(n - 1))/3
全响应 y = (5*(-1)^n)/6 + 2^n/3 + ((-1)^n*(n - 1))/3

2、已知离散系统的系统函数为 ，用MATLAB画出零极点图及系统的幅频特性曲线，并判断系统的稳定性，2018aMATLAB程序如下：

clear
clc
a=[2 0 0 -1];
b=[0 1 -2 -1];
zplane(b,a);
[H,w]=freqz(b,a,100);
mag=abs(H);
phase=angle(H)*180/pi;  %求相频特性，单位为角度
figure;                 %新建图形窗口
plot(w,mag);
xlabel('Frequency(rad)'); 
ylabel('Magnitude');
title('Magnitude response');
figure;                 %新建图形窗口
plot(w,phase);
xlabel('Frequency(rad)'); ylabel('Phase');
title('Phase response');

运行结果如下：
零极点图

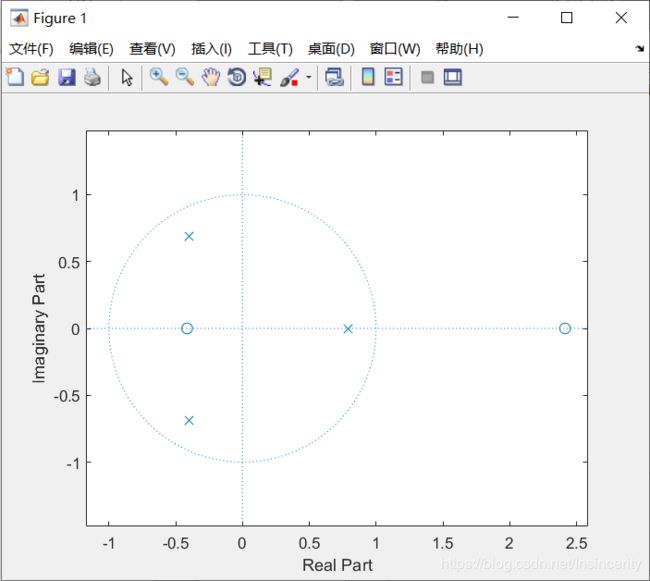
幅频特性曲线


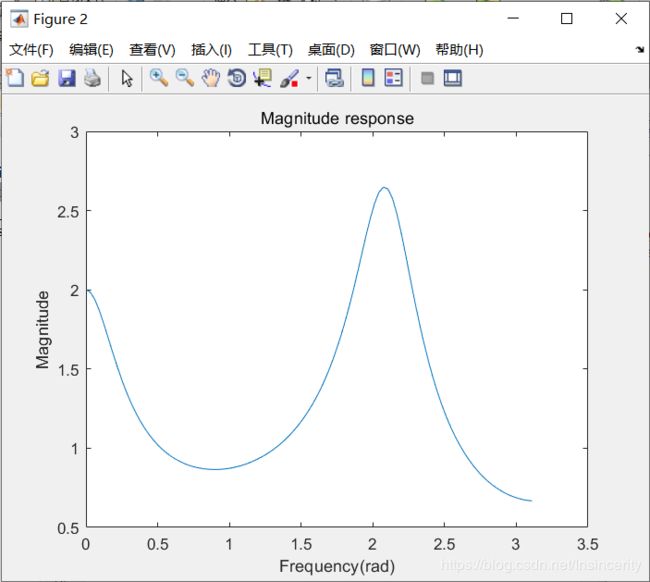
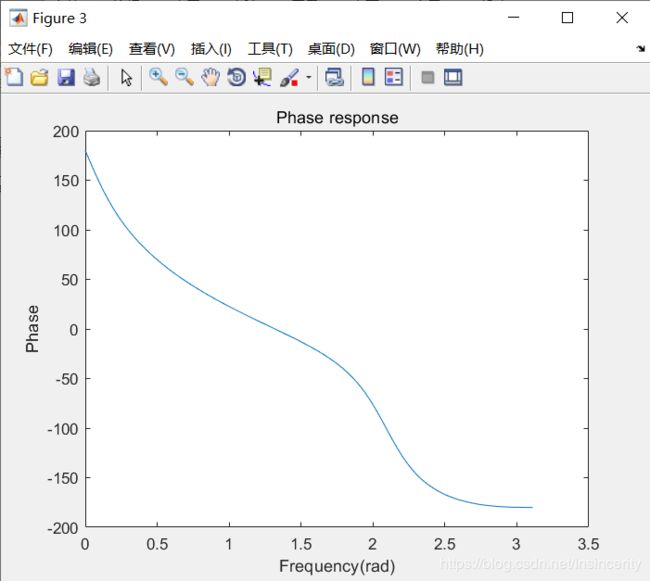
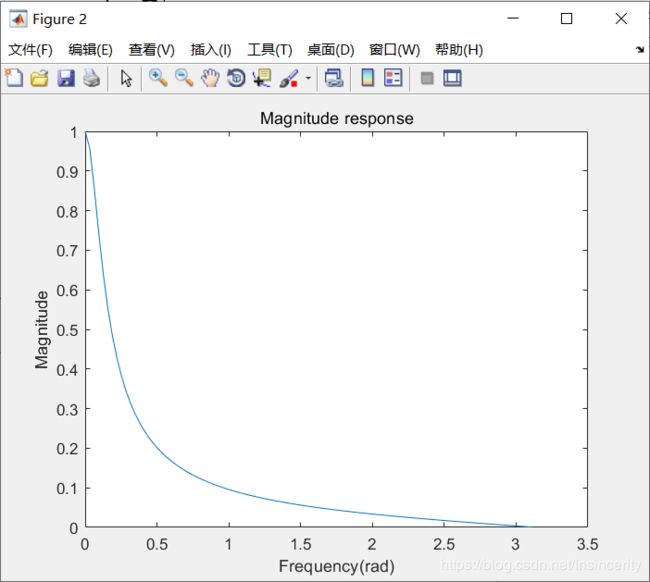
3、根据零极点分布对系统频率特性的影响设计一个单极点单零点、因果实系数低通滤波器H1 (Ω)，满足|H(Ω)|(Ω=0)=1, |H(Ω)|( Ω=π/2)=0.0526, |H(Ω)|( Ω=π)=0，并画出其幅频特性曲线；要求详细列出根据零极点设计滤波器的步骤。
提示：因为所设计的滤波器为单极点单零点、实系数滤波器，所以设该滤波器的系统函数为H(z)=k (z-r)/(z-p)，其中r和p均为实数。
根据要求|H(Ω)|( Ω=0)=1, |H(Ω)|( Ω=π/2)=0.0526, |H(Ω)|( Ω=π)=0;
因为z=e^jΩ，所以可得|H(z)|( z=1)=1, |H(z)|( z=j)=0.0526,|H(z)|( z=-1)=0
所设计滤波器的系统函数为H(z)=k (z-r)/(z-p)=0.0499 (z+1)/(z-0.9002)=0.0499 (1+z^{(-1))/(1-0.9002z}(-1) )=(0.0499+0.0499z^{(-1))/(1-0.9002z}(-1) )=(0.0499z+0.0499)/(z-0.9002)，2018aMATLAB程序如下：

clear
clc
a=[1,-0.9002];
b=[0.0499,0.0499];
zplane(b,a);
[H,w]=freqz(b,a,100);
mag=abs(H);
phase=angle(H)*180/pi; 
figure;
plot(w,mag);
xlabel('Frequency(rad)'); 
ylabel('Magnitude');
title('Magnitude response');
figure;
plot(w,phase);
xlabel('Frequency(rad)'); ylabel('Phase');
title('Phase response');

零极点图

幅频特性曲线