求二叉树中两个节点的最近公共祖先（三叉链，搜索树，普通二叉树）

求二叉树中两个节点的最近公共祖先。

要求：分别考虑以下三种情况
       1、二叉树每个节点有parent（三叉链）
       2、二叉树是搜索二叉树。
       3、就是普通二叉树。（尽可能实现时间复杂度为O（N））

节点：

struct Node
{
    int _data;
    Node* _left;
    Node* _right;
    Node* _parent;

    Node(int x)
        :_data(x)
        , _left(NULL)
        , _right(NULL)
        , _parent(NULL)
    {}
};

一、二叉树每个节点有parent（三叉链）

       这里介绍两种方法并提供代码实现。
第一种方法：
       Node* CommonAncester0(Node* node1, Node* node2)
       把从node1和node2到根节点分别看做两个单链表，定义一个指针tmp游走node2这条链表，node1每走一个节点将node2遍历一遍，同时将tmp->_parent对比，若相等，node1即为公共祖先节点；不相等继续游走。
       代码如下：

Node* CommonAncester0(Node* node1, Node* node2)
{
    if (node1 == NULL || node2 == NULL)
        return NULL;
    Node* tmp = node2;
    while (node1)
    {
        node1 = node1->_parent;
        tmp = node2;
        while (tmp)
        {
            if (node1 == tmp->_parent)
                return node1;
            tmp = tmp->_parent;
        }
    }
    return NULL;
}

第二种方法：
       把从node1和node2到根节点分别看做两个单链表，看做寻找两个相交单链表的交点问题来解决。

       代码：

Node* CommonAncester1(Node* node1, Node* node2)
{
    if (node1 == NULL || node2 == NULL)
        return NULL;
    //先计算链表长度
    int len1 = Length(node1);
    int len2 = Length(node2);
    int sub = 0;
    Node* fast = NULL;
    Node* slow = NULL;

    if (len1 >= len2)
    {
        sub = len1 - len2;
        fast = node1;
        slow = node2;
        while (sub--)
            fast = fast->_parent;
        while (fast)
        {
            if (fast == slow)
                return fast;
            fast = fast->_parent;
            slow = slow->_parent;
        }
    }
    else
    {
        sub = len2 - len1;
        fast = node2;
        slow = node1;
        while (sub--)
            fast = fast->_parent;
        while (fast)
        {
            if (fast == slow)
                return fast;
            fast = fast->_parent;
            slow = slow->_parent;
        }
    }
    return NULL;
}

二、二叉树是搜索二叉树

搜索二叉树特点：
       任意一个节点的左子树的值都小于该节点的值，右子树的值都大于该节点的值。
       从二叉树的根节点开始比较，若两个节点的值都比根节点值大，则公共祖先节点一定在右子树，继续在右子树中用相同方法查找；若都比根节点值小，则公共祖先节点一定在左子树，继续在左子树中查找；若两个节点的值一个大于根节点的值，一个小于根节点的值，则公共祖先节点为根节点。
       代码：

Node* CommonAncester2(Node* root, Node* node1, Node* node2)
{
    if (root == NULL || node1 == NULL || node2 == NULL)
        return NULL;
    if ((root->_data > node1->_data && root->_data < node2->_data) || (root->_data > node2->_data && root->_data < node1->_data))
        return root;
    else if (root->_data < node1->_data && root->_data < node2->_data)
        return CommonAncester2(root->_right, node1, node2);
    else if (root->_data == node1->_data || root->_data == node2->_data)
        return root;
    else
        return CommonAncester2(root->_left, node1, node2);
}

三、普通二叉树

方法1：
       分别找到node1和node2到根节点的路径存储在两个vector中，然后遍历两个vector，直到找到不同的节点。

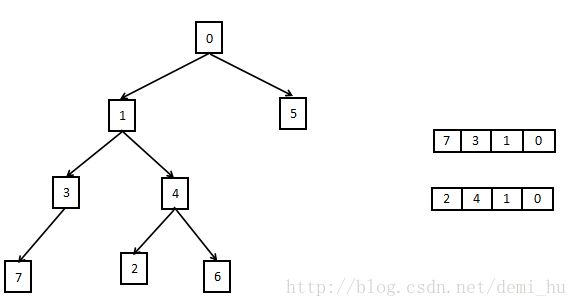
方法2：
       先从根节点开始遍历，若node1或node2中一个与root相同，则根节点即为公共节点；递归查找节点 ，若一个节点在root左子树，一个节点在root右子树，root为公共祖先；如果两个节点都出现在左子树，则说明最低公共祖先在左子树中，否则在右子树。

Node* CommonAncester3(Node* root, Node* node1, Node* node2)
{
    if (root == NULL || node1 == NULL || node2 == NULL)
        return NULL;
    if (node1 == root || node2 == root)
        return root;

    Node* cur = NULL;
    Node* left = CommonAncester3(root->_left, node1, node2);
    if (left)
    {
        cur = CommonAncester3(left->_left, node1, node2);
        if (cur == NULL)
            cur = CommonAncester3(left->_right, node1, node2);
        if ((cur == node1&&left == node2) || (cur == node2&&left == node1))
            return root;
    }

    Node* right = CommonAncester3(root->_right, node1, node2);
    if (right)
    {
        cur = CommonAncester3(right->_left, node1, node2);
        if (cur == NULL)
            cur = CommonAncester3(right->_right, node1, node2);
        if ((cur == node1&&right == node2) || (cur == node2&&right == node1))
            return root;
    }

    if (left&&right)
        return root;
    if (left == NULL)
        return right;
    else
        return left;
}