特征选择方法详解Part2-卡方检验、互信息(Mutual Information)
Content
- 1. 单变量分析
- 1.1 卡方检验
- 1.1.1 原理
- 1.1.2 使用示例
- 1.2 互信息(Mutual Information)
- 1.2.1 原理
- 1.2.1.1 互信息(Mutual Information)
- 定义一
- 定义二
- 定义三
- 1.2.1.2 Normalized Mutual Information
- 1.2.1.3 Adjusted Mutual Information
- 1.2.2 Notice
- 1.2.3 使用示例
- 2. 后续
特征选择系列:
-
特征选择方法详解Part1-方差分析、Pearson、Spearman
-
特征选择方法详解Part2-卡方检验、互信息(Mutual Information)
-
特征选择方法详解Part3-SelectFromModel-RFE、L1、Tree、Permutation importance
在前文《特征选择方法详解Part1-方差分析、Pearson、Spearman》中,详细总结了特征选择的基本方法专家推荐、方差分析和单变量相关性分析方法Pearson、Spearman方法。在本文中将延续Part1的行文结构,介绍单变量相关性分析方法中的卡方检验和互信息方法。
文章同步发在我的个人博客,欢迎大佬们指教。特征选择方法详解Part2-卡方检验、互信息(Mutual Information)
1. 单变量分析
1.1 卡方检验
1.1.1 原理
卡方检验,又称 χ 2 \chi^2 χ2 检验,其用来衡量样本实际观测值与理论推断值之间的偏离程度。在特征工程计算相关性时,理论推断值可以理解为:假设此特征与目标变量(即label)无关,此特征的取值应该服从的分布。(不理解的话直接看下文中例子就明白了)。
先上公式(同样,不想看公式的话直接看下文中例子就明白了):
χ 2 = ∑ i = 1 n ( A − T ) 2 T \chi^2 = \sum_{i=1}^n\frac{(A-T)^2}{T} χ2=i=1∑nT(A−T)2
其中A为实际观测值,T为理论推断值。从上式可以很清晰地看到,计算得到的 χ 2 \chi^2 χ2 值越大,相关性越高。
举个例子就很好明白了:假如现在有一批肿瘤内科患者的数据,想判断患者的收入水平(简单以穷人和富人代替)是否与患者患肠癌有关。简单制作下表表示真实观测值的分布:
| 肠癌患者 | 非肠癌患者 | 总计 | |
|---|---|---|---|
| 穷人 | 67 | 83 | 150 |
| 富人 | 102 | 64 | 166 |
| 总计 | 169 | 147 | 316 |
在上表中四个频数就是卡方检验公式里的A,即A=[67, 83, 102, 64]。
在这个数据中,肠癌患者约占总患者人数的53.48%。如果我们假设患者的收入水平与其患肠癌无关,那理论上,表格应该如下:
| 肠癌患者 | 非肠癌患者 | 总计 | |
|---|---|---|---|
| 穷人 | 150x53.48% ≈ \approx ≈ 80 | 150x46.52% ≈ \approx ≈ 70 | 150 |
| 富人 | 166x53.48% ≈ \approx ≈ 89 | 166x46.52% ≈ \approx ≈ 77 | 166 |
| 总计 | 169 | 147 | 316 |
那么这时候,理论推断值T=[80, 70, 89, 77]。
这下就很明白了,带入卡方检验公式得:
χ 2 = ( 67 − 80 ) 2 80 + ( 83 − 70 ) 2 70 + ( 102 − 89 ) 2 89 + ( 64 − 77 ) 2 77 ≈ 8.62 \chi^2 = \frac{(67-80)^2}{80} + \frac{(83-70)^2}{70} + \frac{(102-89)^2}{89} + \frac{(64-77)^2}{77} \approx 8.62 χ2=80(67−80)2+70(83−70)2+89(102−89)2+77(64−77)2≈8.62
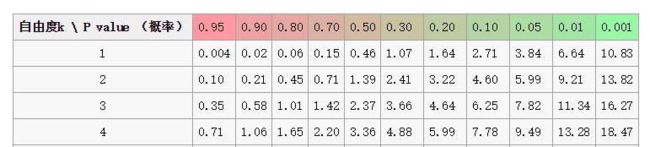
计算得到了 χ 2 \chi^2 χ2 值,如何判断“患者的收入水平与其患肠癌无关”的假设是否成立呢?聪明的人早已整理了卡方分布临界值表,根据 χ 2 \chi^2 χ2 值和其对应的自由度(自由度=(行数 - 1) * (列数 - 1),如上表,行数和列数不计入“总计”列和行。)去表里查一下就可以了(见下图),这个例子中,8.62 > 6.64, 就认为有1%的概率认为“患者的收入水平与其患肠癌无关”的假设成立,即有99%的置信度认为“患者的收入水平与其患肠癌有关”。
上面例子中,使用的变量如收入水平,使用的是离散值,而且从公式可以看到,需要统计频数信息,显然连续变量不适合统计频数。那么问题来了,连续值如何使用卡方检验方法呢? 其实很简单,只需要将连续变量离散化就可以了,想想决策树算法在连续变量上怎么使用的,就是将连续变量的取值范围划分区间,这样每个连续变量的值都有一个区间,就变成离散变量了。使用卡方检验也是一样的道理。
1.1.2 使用示例
sklearn.feature_selection.chi2(X, y)可以计算 χ 2 \chi^2 χ2 值和对应的P-value,但是进行特征选择时,当然不是一个一个计算,而是批量计算。
sklearn.feature_selection提供了 SelectKBest和SelectPercentile方法,看名字就知道,SelectKBest选择前K个最好的特征,SelectPercentile则是按百分比选择特征。这2个方法可选择计算相关性的方法,具体可查看官方文档SelectKBest, SelectPercentile
这里给一个官方示例
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectKBest
>>> from sklearn.feature_selection import chi2
>>> X, y = load_iris(return_X_y=True)
>>> X.shape
(150, 4)
>>> X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
>>> X_new.shape
(150, 2)
1.2 互信息(Mutual Information)
互信息这个方法,真正总结起来,远远比我想象的要复杂。
我仔细阅读了sklearn.feature_select中方法mutual_info_regression、mutual_info_classif的源码、sklearn.metrics中方法mutual_info_score、normalized_mutual_info_score、adjusted_mutual_info_score的源码和互信息的经典论文【A. Kraskov, H. Stogbauer and P. Grassberger, “Estimating mutual information”. Phys. Rev. E69, 2004.】,然后才弄清楚以下几点:
- mutual_info_regression、mutual_info_classif两种方法实现时的区别
- sklearn.feature_select中互信息方法和sklearn.metrics中互信息方法的区别
- 当变量是连续变量的时候,如何计算的(我原先以为是将连续变量划分区间从而实现离散化,实际和我想象的远不一样)
这一小节,我会对上面三个点进行总结性的介绍,如果有时间,我想我会专门写一篇文章详细介绍。
1.2.1 原理
1.2.1.1 互信息(Mutual Information)
定义一
了解决策树的生成过程的话,互信息的理解其实很简单。首先介绍一个概念:信息熵(information entropy),按西瓜书的说法,其是度量样本集合纯度最常用的一种指标。看到“熵”(其物理含义是度量体系混乱程度的指标,值越大越混乱),再看到修饰词“信息”,我想它的含义已经很明确了。这里同样给出其在西瓜书上的公式:
E n t ( D ) = − ∑ k = 1 ∣ Y ∣ p k log 2 p k Ent(D) = -\sum_{k=1}^{|Y|}p_k\log_2p_k Ent(D)=−k=1∑∣Y∣pklog2pk
这里的D可以理解为一个变量(机器学习中可认为其是label,feature都可以定义为D), p k p_k pk 表示向量D中第k个取值所占的比例。Ent(D)值越小,则D纯度越高。
西瓜书中的信息增益(information gain)即是互信息。这里给出互信息的第一个公式(来自西瓜书,变量名修改了下):
G a i n ( Y , X ) = E n t ( Y ) − ∑ v − 1 V ∣ Y v ∣ ∣ Y ∣ E n t ( Y v ) Gain(Y, X) = Ent(Y) - \sum_{v-1}^V\frac{|Y^v|}{|Y|}Ent(Y^v) Gain(Y,X)=Ent(Y)−v−1∑V∣Y∣∣Yv∣Ent(Yv)
式中定义了变量Y和X之间的互信息,这里的 v v v 表示X所有可能取值的编号, Y v Y_v Yv 表示当 x = x v x=x_v x=xv 时,其所对应的Y的值的集合, ∣ Y v ∣ |Y^v| ∣Yv∣ 即表示此集合中的样本数量。举个例子吧,假如 Y = [ 1 , 1 , 0 , 1 ] , X = [ 1 , 2 , 1 , 1 ] Y=[1,1,0,1], X=[1,2,1,1] Y=[1,1,0,1],X=[1,2,1,1] , 这时X的取值有2个:1和2,即 v = [ 0 , 1 ] v=[0, 1] v=[0,1] , 当v=0, 即 x = x 0 = 1 x=x_0=1 x=x0=1 时, ∣ Y v ∣ = [ 1 , 0 , 1 ] |Y^v|=[1,0,1] ∣Yv∣=[1,0,1] , ∣ Y v ∣ = 3 |Y^v|=3 ∣Yv∣=3 .Gain(Y, X) 值越大,说明X和Y相关性越高。
从上面的公式和举例来看,明显X和Y是离散值。如果是连续值的话,可以将X和Y通过划分区间的方式离散化,具体可见西瓜书4.4节。
定义二
直接上公式, 如果X和Y是离散变量:
M I ( X , Y ) = ∑ i = 1 ∣ X ∣ ∑ j = 1 ∣ Y ∣ P ^ ( i , j ) log P ^ ( i , j ) P ( i ) P ( j ) = ∑ i = 1 ∣ X ∣ ∑ j = 1 ∣ Y ∣ ∣ X i ∩ Y j ∣ N log ∣ X i ∩ Y j ∣ / N ∣ X i ∣ / N ⋅ ∣ Y j ∣ / N MI(X,Y)=\sum_{i=1}^{|X|} \sum_{j=1}^{|Y|} \hat P(i,j) \log\frac{\hat P(i,j)}{P(i)P(j)}=\sum_{i=1}^{|X|} \sum_{j=1}^{|Y|} \frac{|X_i\cap Y_j|}{N} \log\frac{|X_i \cap Y_j|/N}{|X_i|/N \cdot |Y_j|/N} MI(X,Y)=i=1∑∣X∣j=1∑∣Y∣P^(i,j)logP(i)P(j)P^(i,j)=i=1∑∣X∣j=1∑∣Y∣N∣Xi∩Yj∣log∣Xi∣/N⋅∣Yj∣/N∣Xi∩Yj∣/N
如果X和Y是连续变量:
M I ( X , Y ) = ∬ f ( x , y ) log f ( x , y ) f ( x ) f ( y ) MI(X,Y)=\iint f(x,y) \log\frac{f(x,y)}{f(x)f(y)} MI(X,Y)=∬f(x,y)logf(x)f(y)f(x,y)
上式中 f ( x , y ) f(x,y) f(x,y) 表示变量X和Y的联合概率密度函数, f ( x ) f(x) f(x) 和 f ( y ) f(y) f(y) 同理。话说这个式子,完全不知道怎么使用。
定义三
直接上公式(来自于我看网上没人写过这个公式,因为很少有人懂吧):
M I ( X , Y ) = Ψ ( k ) − < Ψ ( n x + 1 ) + Ψ ( n y + 1 ) > + Ψ ( N ) MI(X,Y)=\Psi(k)-<\Psi(n_x+1)+\Psi(n_y+1)>+\Psi(N) MI(X,Y)=Ψ(k)−<Ψ(nx+1)+Ψ(ny+1)>+Ψ(N)
上式 Ψ \Psi Ψ 函数是 Gamma函数的导数,scipy.special.digamma可实现其计算;另外 < X > = N − 1 ∑ i = 1 N x i \lt X\gt=N^{-1}\sum_{i=1}^Nx_i <X>=N−1∑i=1Nxi ,上式中k是k近邻算法的参数, n x n_x nx 表示使用X拟合一个k近邻算法后,给定中心点和半径,所有在半径内对数据的个数(我看sklearn上源码是这样算的,论文中也说了,但是没说实现细节), n x n_x nx 同理,N表示样本数。
这个公式引用自互信息的经典论文【A. Kraskov, H. Stogbauer and P. Grassberger, “Estimating mutual information”. Phys. Rev. E69, 2004.】。其从公式二推导而来(推导挺复杂,没看懂)。
为什么要写这个公式呢,sklearn中mutual_info_regression、mutual_info_classif方法在实现时,如果X和Y其中出现连续变量,则使用上式计算的互信息。
1.2.1.2 Normalized Mutual Information
Normalized Mutual Information将互信息归一化到0和1之间,0表示不相关,1表示很完美的相关,这样就更方便比较不同的feature和label的相关程度大小。如下为其公式:
N M I ( X , Y ) = M I ( X , Y ) F ( H ( X ) , H ( Y ) ) , H ( X ) = − E n t ( X ) NMI(X,Y)=\frac{MI(X,Y)}{F(H(X),H(Y))}, H(X)=-Ent(X) NMI(X,Y)=F(H(X),H(Y))MI(X,Y),H(X)=−Ent(X)
上式中 F ( H ( X ) , H ( Y ) ) F(H(X),H(Y)) F(H(X),H(Y)) F表示函数,其可以是均值(mean)、最大值(max)、最小值(min)、均方根函数(sqrt)
1.2.1.3 Adjusted Mutual Information
不管是NMutual Information还是Normalized Mutual Information都有一个缺点:对于离散变量X和Y,如果X和Y的取值越多,那么MI(X,Y)和NMI(X,Y)都倾向于变得更大,而这并不代表X和Y的相关性变得更强。于是,Adjusted Mutual Information应运而生,其公式如下:
A M I ( X , Y ) = M I ( X , Y ) − E ( M I ( X , Y ) ) F ( H ( X ) , H ( Y ) ) − E ( M I ( X , Y ) ) AMI(X, Y)=\frac{MI(X, Y) - E(MI(X, Y))}{F(H(X), H(Y)) - E(MI(X, Y))} AMI(X,Y)=F(H(X),H(Y))−E(MI(X,Y))MI(X,Y)−E(MI(X,Y))
至于上式中的 E ( M I ( X , Y ) ) E(MI(X, Y)) E(MI(X,Y)) 的定义,由于太长且很复杂,这里就不写了(主要自己没理解[捂脸]),给个维基百科的链接吧,有兴趣的朋友可以fan&@¥墙看一下Adjusted Mutual Information)。
1.2.2 Notice
-
不管是NMutual Information还是Normalized Mutual Information都有一个缺点:对于离散变量X和Y,如果X和Y的取值越多,那么MI(X,Y)和NMI(X,Y)都倾向于变得更大,而这并不代表X和Y的相关性变得更强。所以现在使用更多的是Adjusted Mutual Information;
-
sklearn中mutual_info_regression方法在计算互信息时使用的是定义三;
-
sklearn中mutual_info_classif方法在计算互信息时,如果X和Y其中出现连续变量,使用定义三计算互信息,如果都是离散变量,则直接调用sklearn.metrics.mutual_info_score方法,即定义二中的第一个公式;
-
sklearn.metrics中方法mutual_info_score、normalized_mutual_info_score、adjusted_mutual_info_score本意是评价聚类算法效果的,所以这三种算法只支持离散变量。即使输入连续变量也会按照离散变量去计算,导致不正确的结果。
1.2.3 使用示例
sklearn.feature_select中方法mutual_info_regression、mutual_info_classif的使用可见上节卡方检验的使用示例(只需要将方法chi2改成mutual_info_regressionu或mutual_info_classif即可)。
这里给一下sklearn.metrics中方法mutual_info_score、normalized_mutual_info_score、adjusted_mutual_info_score的示例。
>>> import numpy as np
>>> from sklearn.metrics import mutual_info_score, normalized_mutual_info_score, adjusted_mutual_info_score
>>> rng = np.random.RandomState(0)
>>> y1 = rng.randint(0, 10, size=100)
>>> y2 = rng.randint(0, 10, size=100)
>>> y2[:20] = y1[:20]
>>> print("MI")
>>> print(mutual_info_score(y1, y2), mutual_info_score(y1 % 3, y2 % 3))
0.5305136007637552, 0.026551556693229707
>>> print("NMI")
>>> print(normalized_mutual_info_score(y1, y2), normalized_mutual_info_score(y1 % 3, y2 % 3))
0.2381306291604139, 0.0252301499426718
>>> print("AMI")
>>> print(adjusted_mutual_info_score(y1, y2), adjusted_mutual_info_score(y1 % 3, y2 % 3))
0.03389853740628566, 0.0054476031181075295
2. 后续
一下午码了这么多,肯定有一些错字或者遗漏,以后发现再改吧。
写到这里,单变量相关性分析方法就介绍完了。基于模型的特征选择方法可继续看Part3。