HDU第11页（入门）

HDU2000-ASCII码排序

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
bool cmp(int x,int y)
{
	return x>y;
}
int main()
{
	char a[3];
	while(cin>>a)
	{
		sort(a,a+3,cmp);
		for(int i=2;i>=0;i--)
		{
			if(i!=2)
			cout<<" ";
			cout<<a[i];
		}
		cout<<endl;
	} 
	return 0;
}

HDU2001-计算两点间的距离

发现HDU的题和PAT有点差别 比较注重变量类型

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	float x1,y1,x2,y2;
	while(cin>>x1>>y1>>x2>>y2)
	{ 
	float sum=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
	printf("%.2f\n",sum); 
	} 
	return 0;
}

HDU2002-计算球体积

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	double r;
	while(cin>>r)
	{
		double s=3.1415927*r*r*r*4/3;
		printf("%.3f\n",s);
	}
	return 0;
}

HDU2003-求绝对值

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	double n;
	while(cin>>n)
	{
		printf("%.2f\n",abs(n));
	}
	return 0;
}

HDU2004-成绩转换

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	while(cin>>n)
	{
		if(n>100||n<0)
		{
		        printf("Score is error!\n");
		}
		else
		{
		    switch(n/10)
		       {
		        case 10:printf("A\n");break; 
		        case 9: printf("A\n");break;
		        case 8: printf("B\n");break;
		        case 7: printf("C\n");break;
		        case 6: printf("D\n");break;
		        default:printf("E\n");break;
		        }
		}
	}
	return 0;
}

HDU2005-第几天？

第一次没把数组定义放在循环里结果一直WA- -

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int isrunyear(int y)
{
	if((y%400==0&&y%100==0)||(y%4==0&&y%100!=0))
	return 1;
	return 0;
}
int main()
{
	int y,m,d,sum;
	while(scanf("%d/%d/%d",&y,&m,&d)!=EOF)
	{
		int a[12]={31,29,31,30,31,30,31,31,30,31,30,31};
		sum=0;
		if(!isrunyear(y))
		{
			a[1]=28;
		}
		for(int i=0;i<m-1;i++)
		{
			sum+=a[i];
		}
		sum+=d;
		cout<<sum<<endl;
	}
	return 0;
}

HDU2006-求奇数的乘积

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,sum,a;
	while(cin>>n)
	{
		sum=1;
		while(n--)
		{
			cin>>a;
			if(a%2!=0)
			sum*=a;
		}
		cout<<sum<<endl;
	}
	return 0;
}

HDU2007-平方和与立方和

这题唯一骚的地方在于n可能会大于m，所以要加一个if判断

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,m;
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		int sum1=0,sum2=0;
		if(n>m)
		{
			int t;
			t=n;
			n=m;
			m=t;
		}
		for(int i=n;i<=m;i++)
		{
			if(i%2==0)
			sum1+=i*i;
			else
			sum2+=i*i*i;
		}
		cout<<sum1<<" "<<sum2<<endl;
	}
	return 0;
}

HDU2008-数值统计

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,z,f,l;
	float m;
	while(scanf("%d",&n)!=EOF&&n)
	{
		z=f=l=0;
		while(n--)
		{
			cin>>m;
			if(m>0)
			z++;
			else if(!m)
			l++;
			else
			f++;
		}
		cout<<f<<" "<<l<<" "<<z<<endl;
	}
	return 0;
}

HDU2009-求数列的和

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	float n;
	int m;
	while(scanf("%f%d",&n,&m)!=EOF)
	{
		float sum=n;
		for(int i=1;i<m;i++)
		{
			n=sqrt(n);
			sum+=n;
		}
		printf("%.2f\n",sum);
	}
	return 0;
}

HDU2010-水仙花数

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int m,n;
	while(scanf("%d%d",&m,&n)!=EOF)
	{
		int flag=0;
		for(int i=m;i<=n;i++)
		{
			int g=i%10;
			int s=i/10%10;
			int b=i/100%10;
			if(i==g*g*g+s*s*s+b*b*b)
			{
				if(flag)
				cout<<" ";
				flag=1;
				cout<<i; 
			}
		}
		if(!flag)
		cout<<"no";
		cout<<endl;
	}
	return 0;
}

HDU2011-多项式求和

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int m,n;
	float sum;
	while(scanf("%d",&m)!=EOF)
	{
		while(m--)
		{
			cin>>n;
			sum=0;
			for(int i=1;i<=n;i++)
			{
				if(i%2==0)
				sum-=1.0/i;
				else
				sum+=1.0/i;
			}
			printf("%.2f\n",sum);
		}
	}
	return 0;
}

HDU2012-素数判定

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int isprime(int x)
{
	for(int i=2;i<=sqrt(x);i++)
	{
		if(x%i==0)
		return 0;
	}
	return 1;
}
int main()
{
	int x,y;
	while(scanf("%d%d",&x,&y)!=EOF&&(x!=y!=0))
	{	
		int flag=1;
		for(int i=x;i<=y;i++)
		{
			if(!isprime(i*i+i+41))
			{
				flag=0;
				break;
			}
		}
		if(flag)
		cout<<"OK"<<endl;
		else
		cout<<"Sorry"<<endl; 
	}
	return 0;
}

HDU2013-蟠桃记

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int x;
	while(scanf("%d",&x)!=EOF)
	{	
		int s=1;
		for(int i=1;i<x;i++)
		{
			s=(s+1)*2; 
		}
		cout<<s<<endl;
	}
	return 0;
}

HDU2014-青年歌手大奖赛_评委会打分

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int x;
	int a[101],max,min;
	float sum;
	while(scanf("%d",&x)!=EOF)
	{	
		sum=0,max=0,min=100;
		for(int i=0;i<x;i++)
		{
			cin>>a[i];
			if(a[i]>max)
			max=a[i];
			if(a[i]<min)
			min=a[i];
			sum+=a[i];
		}
		sum=sum-max-min;
		printf("%.2f\n",sum/(x-2));
	}
	return 0;
}

HDU2015-偶数求和

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,m;
	int a[101];
	while(scanf("%d%d",&n,&m)!=EOF)
	{	
		for(int i=1,k=2;i<=n;i++,k+=2)
		{
			a[i]=k;
		}
		int s=0,k=n;//用k来标记位置 
		for(int i=1;i<=n;i++)
		{
			s+=a[i];
			if(i%m==0)
			{
				if(k!=n)//判断前面是否输出过数 
				cout<<" ";
				cout<<s/m;
				s=0;
				k-=m;
			}
			else if(k==k%m)
			{
				cout<<" ";
				cout<<s/(k%m);
				s=0;
			}
		}
		cout<<endl;
		
	}
	return 0;
}

HDU2016-数据的交换输出

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,min,k;
	int a[101];
	while(scanf("%d",&n)!=EOF&&n)
	{	
		min=100;
		for(int i=0;i<n;i++)
		{
			cin>>a[i];
			if(a[i]<min)
			{min=a[i];
			k=i;
			}
			
		} 
		int t;
		t=a[k];
		a[k]=a[0];
		a[0]=t;
		for(int i=0;i<n;i++)
		{
			if(i)
			cout<<" ";
			cout<<a[i];
		} 
		cout<<endl;
	} 
	return 0;
}

HDU2017-字符串统计

本来用的string的结果oj提示编译错误- -改成char

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	char s[1111];
	cin>>n;
	while(n--)
	//while(scanf("%d",&n)!=EOF) 这样写会WA
	{	
		cin>>s;
		int sum=0;
		for(int i=0;i<strlen(s);i++)
		{
			if(s[i]>='0'&&s[i]<='9')
			sum++;
		}
		cout<<sum<<endl;
	} 
	return 0;
}

HDU2018-母牛的故事

这题看上去很复杂其实把规律找到你会发现就是个递归 F(n)=F(n-1)+F(n-3)

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	int a[60];
	a[1]=1,a[2]=2,a[3]=3;
	while(scanf("%d",&n)!=EOF&&n)
	{	
		for(int i=4;i<=n;i++)
		{
			a[i]=a[i-1]+a[i-3];
		}
		cout<<a[n]<<endl;
	} 
	return 0;
}

HDU2019-数列有序!

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,m;
	int a[100];
	while(scanf("%d%d",&n,&m)!=EOF&&(n!=0||m!=0))
	{	
		int i;
		for(i=0;i<n;i++)
		{
			cin>>a[i];
		}
		a[i]=m;
		sort(a,a+n+1);
		for(i=0;i<=n;i++)
		{
			if(i)
			cout<<" ";
			cout<<a[i];
		}
		cout<<endl;
	} 
	return 0;
}

HDU2020-绝对值排序

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
bool cmp(int x,int y)
{
	if(x<0)
	x=abs(x);
	if(y<0)
	y=abs(y);
	return x>y;
}
int main()
{
	int n,m;
	int a[100];
	while(scanf("%d",&n)!=EOF&&n)
	{	
		for(int i=0;i<n;i++)
		{
			cin>>a[i];
		}
		sort(a,a+n,cmp);
		for(int i=0;i<n;i++)
		{
			if(i)
			cout<<" ";
			cout<<a[i];
		}
		cout<<endl;
	} 
	return 0;
}

HDU2021-发工资咯：）

这题能算贪心吧 其实只要将每个老师的工资从大到小对各种面值不同的纸币进行除商就好了

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,m;
	int a[6]={100,50,10,5,2,1};
	while(scanf("%d",&n)!=EOF&&n)
	{	
		int s=0;
		while(n--)
		{
			cin>>m;
			for(int i=0;i<6;i++)
			{
				if(m/a[i])
				{
					int k=m/a[i];
					s+=k;
					m=m-k*a[i]; 
				}
			}
		} 
		cout<<s<<endl;
	} 
	return 0;
}

HDU2022-海选女主角

题目描述字很多 大意是在输入的数中找到绝对值最大的数 输出位置和值

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,m,max=0,row,col;
	int a[100][100];
	while(scanf("%d%d",&n,&m)!=EOF)
	{	
		max=0;
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
			{
				cin>>a[i][j];
				if(abs(a[i][j])>max)
				{
					max=abs(a[i][j]);
					row=i;
					col=j;
				}
			}
		}
		cout<<row+1<<" "<<col+1<<" "<<a[row][col]<<endl;
	} 
	return 0;
}

HDU2023-求平均成绩

做题一小时找错一小时- -菜是原罪 提交9次WA7次 罪魁祸首居然是double和float
可恶啊 长记性了

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,m,cnt=0;
	double a[55][6],b[55],c[6];
	while(scanf("%d%d",&n,&m)!=EOF)
	{	
		double sum=0;
		cnt=0;
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
			{
				cin>>a[i][j];
			}
		}
		for(int i=0;i<n;i++)
		{
			sum=0;
			for(int j=0;j<m;j++)
			{
				sum+=a[i][j];
			}
			b[i]=sum/m;
			if(i)
			cout<<" ";
			printf("%.2lf",b[i]);
		}
		cout<<endl;
		for(int i=0;i<m;i++)
		{
			sum=0;
			for(int j=0;j<n;j++)
			{
				sum+=a[j][i];
			}
			c[i]=sum/n;
			if(i)
			cout<<" ";
			printf("%.2lf",c[i]);
		}
		cout<<endl;
		for(int i=0;i<n;i++)
		{
			int flag=1;
			for(int j=0;j<m;j++)
			{
				if(a[i][j]<c[j])
				{
					flag=0;
					break;
				}
			}
			if(flag)
			cnt++;
		}
		cout<<cnt<<endl<<endl;
	}
	return 0;
}

HDU2024-C语言合法标识符

找错半天突然想起来空格会被scanf视为结束- - 用了string 案例是没问题了oj系统维护了明天再提交试试
还是我考虑的太少了以为开头只要不是数字就行但其实除了字母和下划线还会有其他的符号！@ #太菜了

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	char s[1000];
	while(scanf("%d",&n)!=EOF)
	{	
		getchar();
		while(n--)
		{
			gets(s);
			int flag=1;
			if(s[0]>='a'&&s[0]<='z'||s[0]>='A'&&s[0]<='Z'||s[0]=='_') 
			{
				for(int i=1;i<strlen(s);i++)
				{
					
					if(!(s[i]>='a'&&s[i]<='z')&&!(s[i]>='A'&&s[i]<='Z')&&!(s[i]>='0'&&s[i]<='9')&&s[i]!='_')
					{
						flag=0;
						break;
					}
				}
			}
			else
			flag=0;
			if(!flag)
			cout<<"no"<<endl;
			else 
			cout<<"yes"<<endl;
		}
	}
	return 0;
}

HDU2025-查找最大元素

因为看到一位大佬说对于这个题，不用指针来做，就不够专业。用字符数组和字符串函数来做，只能算入门级别的做法。刚好我指针也不太懂就从现在学一下
所以这里给出两种代码
1.利用数组

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	char s[1000];
	while(gets(s))
	{	
		char max='A';
		for(int i=0;i<strlen(s);i++)
		{
			if(s[i]>max)
			{
				max=s[i];
			}
		}
		for(int i=0;i<strlen(s);i++)
		{
			cout<<s[i];
			if(s[i]==max)
			{
				cout<<"(max)";
			}
		}
		cout<<endl;
	}
	return 0;
}

2.利用指针

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	char s[1000],*t;
	while(gets(s))
	{	
		char max='A';
		t=s;
		while(*t)
		{
			if(*t>max)
			max=*t;
			t++;
		}
		t=s;
		while(*t)
		{
			cout<<*t;
			if(*t==max)
			cout<<"(max)";
			t++;
		}
		cout<<endl;
	}
	return 0;
}

HDU2026-首字母变大写

因为上面用了指针所以现在开始多练练指针 说真的看懂和自己会写是不一样的

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	char s[1000],*t;
	while(gets(s))
	{	
		t=s;
		*t-=32;
		t++;
		while(*t)
		{
			cout<<*(t-1);
			if(*(t-1)==' ')
			*t-=32;
			t++;
			if(!*t)
			cout<<*(t-1); 
		}
		cout<<endl;
	}
	return 0;
}

HDU2027-统计元音

这题找错也找了半天- -后来不知道怎么醒的调了一下getchar的位置就A了

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	cin>>n;
	getchar();
	while(n--)
	{
		
		char s[1000],*t;
		gets(s);
		int a,e,i,o,u;
		a=e=i=o=u=0;
		t=s;
		while(*t)
		{
			if(*t=='a')
			a++;
			else if(*t=='e')
			e++;
			else if(*t=='i')
			i++;
			else if(*t=='o')
			o++;
			else if(*t=='u')
			u++;
			t++;
		}
		cout<<"a:"<<a<<endl<<"e:"<<e<<endl<<"i:"<<i<<endl<<"o:"<<o<<endl<<"u:"<<u<<endl;
		if(n)
		cout<<endl;
	}
	return 0;
}

HDU2028-Lowest Common Multiple Plus

这题真的写了太久太久了 看欧几里得算法把我看裂开了 菜到不行- - 其实标准库里有__gcd函数，但是我还是自己写了一个加深记忆
主要思路：根据定理：两数之积等于最小公倍数和最大公约数之积，所以两两求最大公约数后得出最小公倍数，再将这个最小公倍数与后一位数求新的最小公倍数，直至循环结束
不懂欧几里得的可以先去了解一下- -拿来直接用也可以 我是因为有强迫症所以把自己所有不懂的地方都弄懂了才来解题
欧几里得算法

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int gcd(int x,int y)
{
	return y==0?x:gcd(y,x%y);
}
int main()
{
	int n;
	int a[111],sum=1;
	while(cin>>n)
	{
		sum=1;
		memset(a,0,sizeof(a));
		for(int i=0;i<n;i++)
		{
			cin>>a[i];
		}
		int r=gcd(a[0],a[1]);//r为最大公约数 
		int k=a[0]*a[1]/r;//k为最小公倍数 
		for(int i=2;i<n;i++)
		{
			r=gcd(k,a[i]);
			k=k/r*a[i];
		}
		cout<<k<<endl;
		
		
	} 
	return 0;
}

HDU2029-Palindromes _easy version

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	char s[1111];
	cin>>n;
	getchar();
	while(n--)
	{
		gets(s);
		int l=strlen(s);
		int flag=1;
		for(int i=0;i<l;i++)
		{
			if((l%2!=0)&&i==((l-1)/2))
			break;
			if(s[i]!=s[l-i-1])
			{
				flag=0;
				break;
			}
		}
		if(flag)
		cout<<"yes"<<endl;
		else
		cout<<"no"<<endl;
	}
	return 0;
}

HDU2030-汉字统计

本题百度了一下汉字机内码的特点 要注意的是一个汉字为两个字节，他的最高位是1（也就是汉字是由两个负数组成的）知道这个基本就无脑A了 至于为什么最高位是1就得出是负数的结论这个我也不太清楚- -以后再去了解吧

这里解释一下
用二进制的最高位表示数 最高位即最左边的那位
就是二进制的最高位为0表示这是正数,二进制的最高位为1表示 这是负数.
简言之,就是数的符号,0为正,1为负.

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	cin>>n;
	getchar();
	while(n--)
	{
		char s[1000],*t;
		gets(s);
		t=s;
		int cnt=0;
		while(*t)
		{
			if(*t<0)
			{
				cnt++;
			}
			t++;
		}
		cout<<cnt/2<<endl;
	}
	
	
	return 0;
}

HDU2031-进制转换

这是比较低级的算法- -但这确实是我脑子中第一个想到的方法

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n,r,a[100],i;
	while(scanf("%d%d",&n,&r)!=EOF)
	{
		memset(a,0,sizeof(a));
		i=0;
		if(n<0)
		cout<<"-";
		while(n)
		{
			int k=n;
			k%=r;
			a[i]=k;
			i++;
			n/=r;
		}
		for(int j=i-1;j>=0;j--)
		{
			a[j]=abs(a[j]);
			if(r<10||a[j]<10)
			cout<<a[j];
			else
			{
				if(a[j]==10)
				cout<<"A";
				else if(a[j]==11)
				cout<<"B";
				else if(a[j]==12)
				cout<<"C";
				else if(a[j]==13)
				cout<<"D";
				else if(a[j]==14)
				cout<<"E";
				else if(a[j]==15)
				cout<<"F";
			}
		}
		cout<<endl;
	}
	
	return 0;
}

HDU2032-杨辉三角

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	int a[31][31];
	while(cin>>n)
	{
		for(int i=1;i<=n;i++)
		{
			a[i][1]=a[i][i]=1;
		}
		for(int i=3;i<=n;i++)
		{
			for(int j=2;j<i;j++)
			{
				a[i][j]=a[i-1][j-1]+a[i-1][j];
			}
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=i;j++)
			{
				if(j!=1)
				cout<<" ";
				cout<<a[i][j];
			}
			cout<<endl;
		}
		cout<<endl;
	}
	return 0;
}

HDU2033-人见人爱A+B

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	cin>>n;
	int h1,m1,s1,h2,m2,s2,sum1,sum2,sum3;
	while(n--)
	{
		sum1=sum2=sum3=0;
		cin>>h1>>m1>>s1>>h2>>m2>>s2;
		sum1=h1+h2;
		sum2=m1+m2;
		sum3=s1+s2;
		if(sum2>59)
		{
			sum2-=60;
			sum1++;
		}
		if(sum3>59)
		{
			sum3-=60;
			sum2++;
		}
		cout<<sum1<<" "<<sum2<<" "<<sum3<<endl;
	}
	return 0;
}

HDU2034-人见人爱A-B

先去百度了一下集合减法是什么即属于A中A集合但不属于B集合的数 提交的时候居然提示Presentation Error 仔细看看题目发现每个元素后跟一个空格- -
然后题目要求从小到大打印 这里给出使用set容器的代码和普通代码
然后要注意result.end()中存放的是该容器的size(),而不是输入进去的最后一个元素

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
int main()
{
	int n,m,v;
	set<int> result;
	while(cin>>n>>m&&(n!=0||m!=0))
	{
		result.clear();
		for(int i=0;i<n;i++)
		{
			cin>>v;
			result.insert(v);
		}
		for(int i=0;i<m;i++)
		{
			cin>>v;
			if(result.find(v)!=result.end())
			{
				result.erase(v);
			}
		}
		if(result.size()==0)
		cout<<"NULL"<<endl;
		else
		{
			for(set<int>::iterator it=result.begin();it!=result.end();it++)
				cout<<*it<<" ";
			cout<<endl; 
		}
	}
	return 0;
}

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
int main()
{
	int n,m,v;
	while(cin>>n>>m&&(n!=0||m!=0))
	{
		int a[111],v,flag=0;
		for(int i=0;i<n;i++)
		{
			cin>>a[i];
		}
		for(int i=0;i<m;i++)
		{
			cin>>v;
			for(int i=0;i<n;i++)
			{
				if(a[i]==v)
				a[i]=0;
			}
		}
		sort(a,a+n);
		for(int i=0;i<n;i++)
		{
			if(a[i])
			{
				flag=1;
				cout<<a[i]<<" ";
			}
		}
		if(flag)
		cout<<endl;
		else
		cout<<"NULL"<<endl;
	}
	return 0;
}

HDU2035-人见人爱A^B

其实已经是二刷本题了 大一的时候没看懂快速幂随便找了个代码A了 这回算是真看懂了 不懂快速幂的可以先学习一下 写的算是很详细了 我这样的菜鸡都能看懂哈哈哈哈
快速幂取模算法

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
long long Mode(long long a, long long b, long long mode)
{
	long long sum = 1;
	a = a % mode;
 
	while (b > 0) {
		if (b % 2 == 1)		//判断是否是奇数，是奇数的话将多出来的数事先乘入sum
			sum = (sum * a) % mode;
 
		b /= 2;
		a = (a * a) % mode;// 不断的两两合并再取模，减小a和b的规模
	}
	return sum;
}
int main()
{
	int n,m;
	while(cin>>n>>m&&(n!=0||m!=0))
	{
		cout<<Mode(n,m,1000)<<endl;
	}
	return 0;
}

HDU2036-改革春风吹满地

自己的思路感觉有点麻烦- -百度了一下 本题要用到叉积求面积 系统快要开始维护了晚点再看先做下一题
叉积求面积

利用多边形（n边形）面积计算公式：S=0.5 * ( (x0$\ast$y1-x1$\ast$y0) + (x1$\ast$y2-x2$\ast$y1) + … + (xn$\ast$y0-x0$\ast$yn) )，
其中点(x0，y0), (x1， y1), … , (xn，yn)为多边形上按逆时针顺序的顶点（（x0，y0）与（xn，yn）为同一点）。
注意最后要另外加上第一个点和第n个点的叉积

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
struct point
{
	int x,y;
}N[100];
int main()
{
	int n;
	while(cin>>n&&n)
	{
		double sum=0;
		for(int i=0;i<n;i++)
		{
			cin>>N[i].x>>N[i].y;
		}
		for(int i=1;i<n;i++)
		{
			sum+=(N[i].x*N[i-1].y-N[i].y*N[i-1].x);
		}
		sum+=(N[0].x*N[n-1].y-N[n-1].x*N[0].y);
		printf("%.1lf\n",abs(sum)*0.5);
	}
	return 0;
}

HDU2037-今年暑假不AC

一道贪心 本题要求看的节目数量尽可能的多，分析题目后办法之一是在一个节目看完后马上接下一个 那么要实现的话其实只要将每个节目的结束时间进行排序 然后递归比较下一个节目的开始时间是否大于上一个节目的结束时间 如果是 即节目数加一 看完后记得将时间调整为这个节目的结束时间
其实我的贪心也烂的一笔 思路也是看大佬的代码才得出的- -

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
struct times
{	
	int b,e;
}N[101];
bool cmp(times x,times y)
{
	return x.e<y.e;
}
int main()
{
	int n,m;
	while(cin>>n&&n)
	{
		for(int i=0;i<n;i++)
		{
			cin>>N[i].b>>N[i].e; 
		}
		sort(N,N+n,cmp);
		int cnt=1,k=N[0].e;
		for(int i=1;i<n;i++)
		{
			if(N[i].b>=k)
			{
				cnt++;
				k=N[i].e;
			}
		}
		cout<<cnt<<endl;
	}
	return 0;
}

HDU2039-三角形

2038不见了- -
第一次提交WA百度了一下发现题目说是正数没说是整数- - 太粗心
因为a+b>c&&a+c>b&&c+b>a不等式交换就是a-b 所以代码可以再优化

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
int istriangle(double x,double y,double z)
{
	if(x+y>z&&x+z>y&&z+y>x)
	return 1;
	return 0;
}
int main()
{
	int n;
	double x,y,z;
	cin>>n;
	while(n--)
	{
		cin>>x>>y>>z;
		if(istriangle(x,y,z))
		cout<<"YES"<<endl;
		else
		cout<<"NO"<<endl; 
	}
	return 0;
}

HDU2040-亲和数

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
long isqinhe(int x)
{
	int sum=0;
	for(int i=1;i<=sqrt(x);i++)
	{
		if(x%i==0&&(i!=x/i))
		sum+=i+x/i;
		else if(x%i==0)
		sum+=i;
	}
	return sum-x;
}
int main()
{
	int n,a,b;
	cin>>n;
	while(n--)
	{
		cin>>a>>b;
		if(a==isqinhe(b)&&b==isqinhe(a))
		cout<<"YES"<<endl;
		else
		cout<<"NO"<<endl;
	}
	return 0;
}

HDU2041-超级楼梯

其实这一道题就是一道斐波拉契数列的题目！我们可以分析一下！因为它只能跨上一级或二级，所以到达我们这一层的走法就是前1阶的走法（再走一步就到我们啦）以及前2阶的走法（再走一步就到我们了！）注意！不能选走两次一步的！因为我们走了一次一步，那就是到达我们的前1阶，这样子就是我们前面（前1阶的走法里面包含了的）。

这道题还有两个小坑，那就是我们一开始就是处于第一阶，在计算的时候要注意一下。还有一个bug是如果m=1 理应输出0 但oj系统上输出0和1都是没问题的

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
int main()
{
	int n,m;
	int a[40];
	a[1]=1,a[2]=1,a[3]=2;
	cin>>n;
	while(n--)
	{
		int sum=0;
		cin>>m;
		for(int i=4;i<=m;i++)
		{
			a[i]=a[i-1]+a[i-2];
		}
		cout<<a[m]<<endl;
	}
	return 0;
}

HDU2042-不容易系列之二

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
int main()
{
	int n,m,sum=3;
	cin>>n;
	while(n--)
	{
		cin>>m;
		sum=3;
		while(m--)
		{
			sum=(sum-1)*2;
		}
		cout<<sum<<endl;
	}
	return 0;
}

HDU2043-密码

变量用的有点多- -怀疑是自己太菜了

#include
#include
#include
#include
#include
#include 
#include 
#include
using namespace std;
int main()
{
	int n;;
	cin>>n;
	getchar();
	while(n--)
	{
		char s[50],*t;
		gets(s);
		t=s;
		int cnt=0,flag=1,flag1=0,flag2=0,flag3=0,flag4=0;
		while(*t)
		{
			if(strlen(s)>=8&&strlen(s)<16)
			{
				if(*t>='a'&&*t<='z'&&!flag1)
				{cnt++;flag1=1;}
				else if(*t>='A'&&*t<='Z'&&!flag2)
				{cnt++;flag2=1;}
				else if(*t>='0'&&*t<='9'&&!flag3)
				{cnt++;flag3=1;}
				else if((*t=='~'||*t=='!'||*t=='@'||*t=='#'||*t=='$'||*t=='%'||*t=='^')&&!flag4)
				{cnt++;flag4=1;}
				t++;
				if(cnt==3)
				break; 
			}
			else
			{
				flag=0;
				break;
			}
			
			
		}
		if(cnt>=3)
		{
			cout<<"YES"<<endl;
		}
		else if(!flag)
		cout<<"NO"<<endl;
		else 
		cout<<"NO"<<endl;
	}
	return 0;
}

HDU2044-一只小蜜蜂…

看了大神的分析感觉自己菜到烂开

这个问题非常类似于：HDU2041 超级楼梯，略微有些不同。

站在第n个蜂房想一下，前一步是从哪里来的，问题就清楚了。

看图可知，由于蜜蜂每次只能从前1个蜂房前2个蜂房过来，那么f(n)=f(n-2)+f(n-1)。这部就是一个斐波那契数列吗？就是一个递推问题？

可是，开始时候，蜜蜂是在第1个蜂房，所以数列的开始几项会有所不同。

f(1)=0，因为蜜蜂开始在第1个蜂房；

f(2)=1，蜜蜂只能从第1个蜂房来到第2个蜂房；

f(3)=2，蜜蜂可以从第1个蜂房过来，也可以从第2个蜂房过来；

f(n)=f(n-2)+f(n-1)，n>3。

有了以上的递推式，一切几乎就解决了。

还需要考虑的一点是，蜜蜂从a蜂房到b蜂房的各种可能路径，相当于从第1蜂房到第b-a+1蜂房。

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	int n,a,b;
	ll arr[50];//int不够装
	cin>>n;
	while(n--)
	{
		cin>>a>>b;
		arr[1]=0;arr[2]=1;arr[3]=2;
		for(int i=4;i<=b;i++)
		{
			arr[i]=arr[i-1]+arr[i-2];
			
		}
		cout<<arr[b-a+1]<<endl;
	} 
	return 0;
}

HDU-2045- 不容易系列之(3)—— LELE的RPG难题

牛皮 我是真的没想到这种思路 心疼的抱抱自己

这题的难度主要在递推公式的找寻，一般从最后开始找规律。
思路如下：

n个方格的涂色方案可以由n - 1的涂色方案追加一个得出，分两种情况：

1.在n - 1的合法涂色方案后追加一个方格，由于合法方案的首尾颜色不同，因此第n个方格的颜色必定是这两种颜色之外的一种，即方案数为f[n - 1]。
2.在n - 1的不合法涂色方案（首尾颜色相同）后追加一个合法的涂色方格，也可能使其成为长度为n的合法涂色方案，而这种不合法涂色方案的结构必定是f[n - 2]合法方案 + 首格颜色 + 首格外的两种颜色，即方案数为2 * f[n - 2]。

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	int n;
	ll a[50];
	a[1]=3;a[2]=6;a[3]=6;
	while(cin>>n)
	{
		for(int i=4;i<=n;i++)
		{
			a[i]=a[i-1]+a[i-2]*2;
		}
		cout<<a[n]<<endl;
	} 
	return 0;
}

HDU-2046-骨牌铺方格

解题思路：在我们知道这是一道递推的题目后，当长方形方格为2×n时，我们应该要想到骨牌的铺放方案是从2×（n-1）和2×（n-2）中的铺放方案中来的。我们用f(n)表示当骨牌数为n时的铺放方法数目。
骨牌数目为n时相当于是在骨牌数为（n-1）的尾端增加了一张竖牌；同时也相当于在骨牌数为（n-2）的尾端增加了两张横牌（大家可以动手稍微画一下，想一下就明白了）。记住不能再算竖牌，不然就和（n-1）的那种重复了。

用算式表示就是：f(n) = f(n-1) + f(n-2)。即斐波拉契数列。

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	int n;
	ll a[50];
	a[1]=1;a[2]=2;a[3]=3;
	while(cin>>n)
	{
		for(int i=4;i<=n;i++)
		{
			a[i]=a[i-1]+a[i-2];
		}
		cout<<a[n]<<endl;
	} 
	return 0;
}

HDU-2047-阿牛的EOF牛肉串

这次是自己试着推的因为前面都是从后面推起那我们也从后面开始分析
当F[n]等于O时 要求F[n-1]不为O 即有F[n]=F[n-2]*2
当F[n]不等于O时 F[n]=F[n-1]*2
综上所述 F[n]=F[n-1]*2+F[n-2]*2

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	int n;
	ll a[50];
	a[1]=3;a[2]=8;
	while(cin>>n)
	{
		for(int i=3;i<=n;i++)
		{
			a[i]=a[i-1]*2+a[i-2]*2;
		}
		cout<<a[n]<<endl;
	} 
	return 0;
}

HDU-2048-神、上帝以及老天爷

这道题实际上就是让我们求：当所有人都拿不到自己所对应的号时的可能性，典型的错排问题

本题思路：
假设有n-1个人完全错排，而第n个人手上拿到的是自己名字 那么这个人与前面n-1个人每个人交换一次即可达到n个人完全错排即F(n-1)$\ast$(n-1）
假设在前n-1个人中也有一个人拿到的是自己名字，那么这个人与第n个人交换即可达到完全错排即(n-1)*F(n-2)
综上即F(n)=(n-1)$\ast$(F(n-1)+F(n-2))
全错的概率 = 全错数 / 全部情况。
全部情况就是N的阶乘。
WA五遍- -检查发现是数组开小了

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
double factorial(int x)
{
	double sum=1;
	for(int i=1;i<=x;i++)
	{
		sum*=i;
	}
	return sum;
}
int main()
{
	ll a[20];
	int n;
	cin>>n;
	int k;
	a[1]=0;a[2]=1;a[3]=2;
	while(n--)
	{
		cin>>k;
		for(int i=4;i<=k;i++)
		{
			a[i]=(i-1)*(a[i-1]+a[i-2]);
		}
		printf("%.2lf%%\n",a[k]/factorial(k)*100);
	}
	return 0;
}

HDU-2049-不容易系列之(4)——考新郎

这道题其实就是上一道题的衍生 在N个数中M个数有多少种错排方法
即高中的排列组合问题

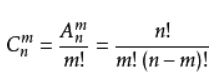
这里要注意阶乘函数定义需要用long long 因为20！已经是2432902008176640000了

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
ll factorial(int x)
{
	double sum=1;
	for(int i=1;i<=x;i++)
	{
		sum*=i;
	}
	return sum;
}
int main()
{
	ll a[21];
	int c;
	cin>>c;
	int m,n;
	a[1]=0;a[2]=1;a[3]=2;
	while(c--)
	{
		cin>>n>>m;
		for(int i=4;i<=m;i++)
		{
			a[i]=(i-1)*(a[i-1]+a[i-2]);
		}
		cout<<factorial(n)/factorial(m)/factorial(n-m)*a[m]<<endl;
	}
	return 0;
}

HDU-2050-折线分割平面

不会沃日 下一题先

HDU-2051-Bitset

简单的十进制转二进制

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	int n,a[1001],cnt=0;
	while(cin>>n)
	{
		cnt=0;
		int i=0;
		while(n)
		{
			a[i]=n%2;
			n/=2;
			cnt++;
			i++;
		}
		for(int i=cnt-1;i>=0;i--)
		cout<<a[i];
		cout<<endl;
	}
	return 0;
}

HDU-2052-Picture

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	int n,m;
	while(cin>>n>>m)
	{
		cout<<'+';
		for(int i=1;i<=n;i++)
		{
			cout<<'-';
		}
		cout<<'+'<<endl;
		for(int i=1;i<=m;i++)
		{
			cout<<'|';
			for(int j=1;j<=n;j++)
			{
				cout<<' ';
			}
			cout<<'|'<<endl;
		} 
		cout<<'+';
		for(int i=1;i<=n;i++)
		{
			cout<<'-';
		}
		cout<<'+'<<endl<<endl;
	}
	return 0;
}

HDU-2053-Switch Game

题意：有一些灯排成一条直线。所有的灯在刚开始都是关闭的，在对灯进行一系列操作后:在第 i 次操作的时候，调整所有标号是 i 的倍数的灯的状态(原本打开的灯将它关闭，原本关闭的将它打开)。
本来按照我清晰的思路写 结果超时了- - 百度了一下
判断第n盏灯的状态只要判断n的被操作次数即n的因数个数 比如n=10 那么在1、2、5、10次操作时会操作n灯 偶数次就是关闭0 奇数次就是打开1

//其实这里可以缩短时间 循环到sqrt(n)即可
//但题目要求不大我嫌麻烦就写个快一点的了
#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	while(cin>>n)
	{
		int sum=0;
		for(int i=1;i<=n;i++)
		{
			if(n%i==0)
			sum++;
		}
		if(sum%2==1)
		cout<<"1"<<endl;
		else
		cout<<"0"<<endl; 
	}
	return 0;
}

HDU-2054-A == B ?

看着这题通过率巨低我就试着做了一下 果然涉及到字符的题目都巨麻烦- - 提交好几次没A掉最后发现是数组开小了cao 看了看时间现在都1点了沃日

写的时候就一直担心会超时什么的 还好不用去前导0题目没有对001和1这种进行要求 还算有点人性 要是再写段去前导0我感觉必超时- -说白了还是算法效率太低
我的去小数点后0的思路是记录下最后一个不为0的数的位置，还有一种方法是从最后一位开始 如果为0就换成’\0’结束符 这种简单点

试了几次WA之后，终于AC了，其实很简单，但是需要严谨。

思路：这题由于没有给出条件，因此会出现上千甚至上万位数的测试数据，于是必须用字符串来解题。

然后难点就是去除小数点后不为零数字后面的0，实际上就这两点而已。

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	char n[111111],m[111111];
	while(cin>>n>>m)
	{
		int flag=1,n1,m1,flagn=0,flagm=0;
		int len1=strlen(n),len2=strlen(m);
		for(int i=0;i<strlen(n);i++)
		{
			if(n[i]=='.')
			{
				n1=i+1;
				len1=n1-1;
				break;
			}
		}
		for(int i=0;i<strlen(m);i++)
		{
			if(m[i]=='.')
			{
				m1=i+1;
				len2=m1-1;
				break;
			}
		}
		for(int i=n1;i<strlen(n);i++)
		{
			if(n[i]!='0')
			{
				flagn=1;
			}
			else
			flagn=0;
			if(flagn==1)
			len1=i+1;
		}
		for(int i=m1;i<strlen(m);i++)
		{
			if(m[i]!='0')
			{
				flagm=1;
			}
			else
			flagm=0;
			if(flagm==1)
			len2=i+1;
		}
		if(len1!=len2)
		{
			cout<<"NO"<<endl;
		}
		else
		{
			for(int i=0;i<len1;i++)
			{
				if(n[i]!=m[i])
				{
					cout<<"NO"<<endl;
					flag=0;
					break;
				}
			}
			if(flag)
			cout<<"YES"<<endl;
		}
	}
	return 0;
}

HDU-2055-An easy problem

第一遍落了=号 WA了- -还好马上看到了

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
int main()
{
	int n;
	cin>>n;
	while(n--)
	{
		int y;
		char x;
		cin>>x>>y;
		if(x>='A'&&x<='Z')
		cout<<x-64+y<<endl;
		if(x>='a'&&x<='z')
		cout<<(x-96)*-1+y<<endl;
	}
	return 0;
}

HDU-2056-Rectangles

1

HDU-2057-A + B Again

本来想手动模拟十六进制加法的然后在考虑怎么输入的问题 百度了一下发现新的方法- -

注意：十六进制输入十六进制输出就ok。
题目告知A长度不会超过15位，A最大为fffffffffffffff，转换成10进制为 1152921504606847046，long long范围是-$2^{63}$~ +$2^{63}$-1, +MAX: 9223372036854775807，所以long long足够了。

需要注意的是如果用long long，输入和输入时都需要写成 %llX
，%x和%X分别对应十六进制中字母小写和字母大写，需要对结果<0时做一些处理，这样就AC了~

附带：
格式字符 格式字符意义 
d   以十进制形式输出带符号整数(正数不输出符号) 
o   以八进制形式输出无符号整数(不输出前缀O) 
x   以十六进制形式输出无符号整数(不输出前缀OX) 
u   以十进制形式输出无符号整数 
f   以小数形式输出单、双精度实数 
e   以指数形式输出单、双精度实数 
g   以%f%e中较短的输出宽度输出单、双精度实数 
c   输出单个字符 
s   输出字符串

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	ll a,b;
	while(scanf("%llx %llx",&a,&b)!=EOF)
	{
		if(a+b>=0)
		printf("%llX\n",a+b);
		else
		printf("-%llX\n",-(a+b));
	}
	return 0;
}

HDU-2068-RPG的错排

这两天状态不对- -越来越不想学了完蛋
思路：错排计数。错位排列的公式有dn=n!(1-1/1!+1/2!-1/3!+…+(-1)^$n\ast 1$/n!) 还有一个递推的形式 d[n]=(n-1)*(d[n-1]+d[n-2]) 。其中 d[0]=1 d[1]=0 d[2]=1;这里采用第二种形式。对于N个数全排列，要求不是错排的个数大于或等于n的一半，也就是错排的个数小于或等于n的一半，即错排的个数 从0到n/2 ，对每个错排的个数都有C（n,i）种选择，i为错排的个数，在n个数中挑i个来错排，$c(n,i)\ast d[i]$ 即每种错排情况的个数，累加起来即可。

#include
#include
#include
#include
#include
#include 
#include
using namespace std;
typedef long long ll;
int main()
{
	int n;
	ll a[25],b[26][26];
	for(int i=0;i<=25;i++)
	{
		b[i][0]=b[i][i]=1;
	}
	for(int i=2;i<=25;i++)
	{
		for(int j=1;j<i;j++)
		{
			b[i][j]=b[i-1][j]+b[i-1][j-1];
		}
	}
	while(cin>>n&&n)
	{
		a[0]=1;a[1]=0;a[2]=1;a[3]=2;
		for(int i=4;i<14;i++)
		{
			a[i]=(i-1)*(a[i-1]+a[i-2]);
		}
		ll sum=0;
		for(int i=0;i<=n/2;i++)
		{
			sum+=a[i]*b[n][i];
		}
		cout<<sum<<endl;
	}
	return 0;
}