使用STM32做FFT

如何使用ARM做FFT变换？如何将FFT的变换结果还原成幅度、频率等具有实际物理意义的数值呢？本文和大家一起探讨些这些问题。本文硬件使用GFARM02硬件模块[1]，文章最后有其淘宝链接。核心器件为STM32F103RCT6，为Cortex-M3核，采用的CMSIS版本为CMSIS_5-5.6.0。

ARM官方库函数

这里我们使用ARM官方的库函数进行FFT变换，该库支持复数FFT，当前复数 FFT 函数支持浮点类型， Q31 和 Q15类型。 有待分析的数据存放在一个输入数组中，为了节省空间，这些 FFT 函数将FFT的变换结果覆盖在输入数组中，数组的顺序均为：实部、虚部、实部、虚部…

浮点型复数FFT函数

浮点型复数FFT函数：

// 微信：GuoFengDianZi
#define TEST_LENGTH_SAMPLES 2048

uint32_t fftSize = 1024;
uint32_t ifftFlag = 0; //IFFT还是FFT运算,为0表示FFT
uint32_t doBitReverse = 1; //是否位反转
static float32_t testInput_50Hz_1khzSampling[TEST_LENGTH_SAMPLES];

arm_cfft_f32(&arm_cfft_sR_f32_len1024, testInput_50Hz_1khzSampling, ifftFlag, doBitReverse);
//arm_cfft_sR_f32_len1024代表进行1024点的FFT变换
//testInput_50Hz_1khzSampling是采样后得到的数组（数组的顺序均为：实部、虚部、实部、虚部......）

除了FFT之外，库还提供了求解复数模值的函数：

// An highlighted block
arm_cmplx_mag_f32(testInput_50Hz_1khzSampling, testOutput, NumSamples);
//testInput_50Hz_1khzSampling:有待求解的复数数组
//testOutput：存放输出数据的数组
//NumSamples：复数的个数

借助这两个函数我们可以进行FFT的分析了。

将FFT结果还原成幅度和频率

若采样频率为 Fs，信号频率 F，采样点数为 N，那么某点 n 所表示的频率为：
Fn=(n-1)*Fs/N; （假设n从1开始计数）
若FFT变换后第n点的幅度值为An，则对应的实际物理幅度数值：
A=An/(N/2);
运用上述公式即可将FFT结果和实际物理量对应起来。

编程实验1：FFT运算验证

// 满洲里国峰电子科技
// 微信：GuoFengDianZi
float32_t SampleFreq=1000;//以1kHz速率采样
// 模拟一个采样数组
for(i=0; i<fftSize; i++)
{       // 虚部为0
		testInput_50Hz_1khzSampling[i*2+1] = 0;
		// 将一个10Hz正弦波按照采样频率采样，存入实部
		testInput_50Hz_1khzSampling[i*2] = arm_sin_f32(2*3.1415926f*10*i/SampleFreq);
}

  //调用复数傅里叶变换
  arm_cfft_f32(&arm_cfft_sR_f32_len1024, testInput_50Hz_1khzSampling, ifftFlag, doBitReverse);
  //计算FFT幅度值
  arm_cmplx_mag_f32(testInput_50Hz_1khzSampling, testOutput, fftSize);
  //找到最大幅度值以及其对应的数组位置（下标）
  arm_max_f32(testOutput, fftSize, &maxValue, &testIndex);
  //找到并计算最大的幅度值
  maxValue=CalFirstPeakMag(maxValue, fftSize);
  printf("maxvalue=%f \r\n",maxValue);
  //找到最大的幅度值对应的频率值	
  PeakFreq=CalFirstPeakFreq(SampleFreq, fftSize, testIndex);
  printf("Freq=%f \r\n",PeakFreq);

使用串口助手打印的结果为：

在上述代码中我们的输入信号是幅度值为1、频率10Hz的正弦波，经过FFT分析后，我们计算得出其幅度值为0.9066，频率为9.766，在合理的区间，但存在差别，这就是频谱泄露。

频谱泄露

通过上面的实验我们基本可以使用STM32做FFT变换了。但是我们发现精确度还可以在提高，这里就涉及到频谱泄露的概念。

FFT是DFT的快速算法，而DFT只能计算有限的时域数据，如果这个有限的时域数据刚好是完整的波形如下图所示，那么就不会出现频谱泄露。

但是如果这个有限的时域数据并不是整数个波形，那么就会产生频谱泄露。如下图所示的波形就会产生频谱泄露。

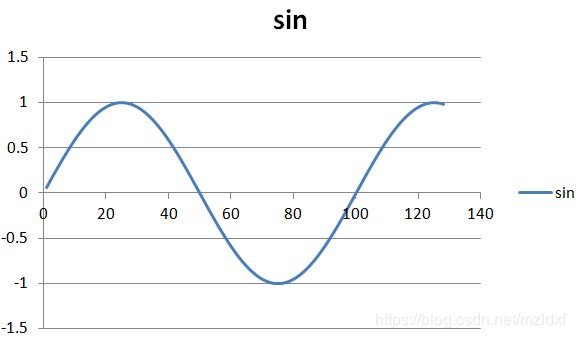
所谓频谱泄露就是主瓣的能量被旁瓣分走了，所以实验得到的幅值不是1，而是0.9。

针对频谱泄露，应尽量使用完整时域波形进行分析，再根据需要选择合适的窗函数来加以改善。

增加FFT点数、同时增加信号的周期数

对一个5Hz的正弦信号用60Hz采样速率采样，分别采样64、128、256、512、1024个点，并分别进行64、128、256、512、1024点FFT运算并对比结果，64bit FFT部分代码如下:

//满洲里国峰电子科技
//微信：GuoFengDianZi
#define TEST_LENGTH_SAMPLES 128
uint32_t fftSize = 64;
float32_t SampleFreq=60;//采样频率60Hz
for(i=0; i<fftSize; i++)
{
	testInput_Sampling[i*2+1] = 0;
	testInput_Sampling[i*2] = 1*arm_sin_f32(2*3.1415926f*5*i/SampleFreq);
}
  /* Process the data through the CFFT/CIFFT module */
  arm_cfft_f32(&arm_cfft_sR_f32_len64, testInput_Sampling, ifftFlag, doBitReverse);
  /* Process the data through the Complex Magnitude Module for
  calculating the magnitude at each bin */
  arm_cmplx_mag_f32(testInput_Sampling, testOutput, fftSize);

具体的函数解释，见博客：《使用STM32做FFT》，链接：https://blog.csdn.net/mzldxf/article/details/104101094
实验结果如下图所示，maxvalue表示频谱最高峰的峰值，Freq表示该峰值对应的频率，可见随着FFT点数和采样点数的同时增加（由于采样频率不变，意味着被采样的时域信号的周期数增加），频率的精确度越来越高（由于矩形窗的幅度识别度不高，而频率的识别精度高，所以我们观察频率）。

将多出的采样点置零？

如果我们采用64Bit FFT，采样点数也是64个，采样频率为50Hz，待测信号为1Hz，这样的话，一个周期内的采样点数是50个，最后14个点采样的是下个周期的，我们通过下面的代码将其置零，然后做FFT看效果如何？

	for(i=60; i<64; i++)
		testInput_Sampling[i*2]=0;

两次计算获得的数值一样，可见这样的做法没有什么帮助。

频谱分辨率

FFT的频谱分辨率由采样点数N和采样频率Fs决定：
频谱分辨率=Fs/N
例如我们想用FFT分析这样一个信号：
1.2$\times$arm_sin_f32(2$\times$ 3.1415926f $\times$ 5.5$\times$ i/SampleFreq)
其频率为5.5Hz，如果使用SampleFreq=64，fftSize = 64就得不到正确的结果。而使用SampleFreq=32，fftSize = 64就可以，这是因为虽然第二种采样频率低了，但是其频率分辨率更高。

DFT的由来–时域与频域的从连续到离散

//注：下面一段摘自维基百科，稍作了润色和修改，原文见[2]
自然界中的时间信号$x(t)$通常是连续的，对应的连续傅里叶变换$\hat{x}(\omega )$ 也是连续函数。由于数字处理器只能处理有限长的离散信号，因此必须将 $x(t)$和 $\hat{x}(\omega )$ 都离散化，并且建立对应的傅里叶变换，数字处理器才能够处理。[2]

首先，时域采样将$x(t)$离散化，这一过程对应着ADC采样。

其傅里叶变换为：（这一过程称之为：离散时间傅里叶变换DTFT）

需要注意的是${\hat{x}}_{discrete}(\omega )$ 仍然是连续的，数字处理器仍然处理不了，为此需要对其进行“频域离散化”，对其在频域上采样：

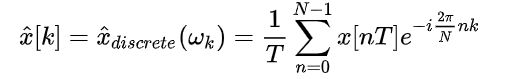
归一化后就是我们的DFT：

因此，通俗的说，DFT是为了处理自然界中模拟连续的物理量，将该物理量在时域、频域离散化后的结果。

使用公式产生正弦信号采样点

/* 50Hz, sampling rate: 1024Hz */
testInput_50Hz_1khzSampling[i*2] = 1.6*arm_sin_f32(2*3.1415926f*50*i/SampleFreq);

/****************************************************************************************/

作者：伏熊（专业：射频芯片设计、雷达系统、嵌入式。欢迎大家项目合作交流。）
微信：GuoFengDianZi

/****************************************************************************************/
笔者使用硬件淘宝店链接：
[1]https://item.taobao.com/item.htm?spm=a2126o.11854294.0.0.67154831RZohYn&id=611784950993

引用：
[2]https://zh.wikipedia.org/wiki/%E7%A6%BB%E6%95%A3%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2, 2020年1月28日