数据结构刷题记录--编程题

1（链表）

解析：我们可以修改给定节点之前的指针，使它指向该节点的下一个节点，但是我们无法访问该节点之前的位置，无法修改，所以我们需要将该节点的数据更改为后面节点的数据，然后删除该节点后面的节点，如果要删除的节点是末尾节点，则不能这样做

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public void deleteNode(ListNode node) {
        node.val = node.next.val;					//更改该节点的值=后面节点的值
        node.next = node.next.next;				//使该节点直接指向后面的节点后面的节点
    }
}

2.（链表）

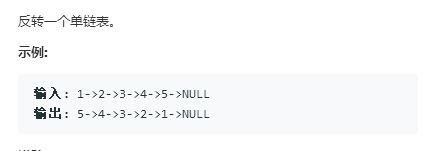
解析：我们需要定义一个新的指针指向第一个节点的前一个位置赋值为空，使用循环将后一个节点指向前一个节点，并将两个节点的指针后移，当当前指针指向空时，循环结束。

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;        //当前节点的上一个节点，初始为空
        ListNode cur = head;        //当前节点，初始为头结点
        while(cur != null){
            ListNode temp = cur.next;     //代表当前节点的下一个节点，用来将当前节点指针后移  
            cur.next = pre;               //使当前节点指向前一个节点
            pre = cur;                    //前一个节点指针后移
            cur = temp;                   //当前节点指针后移
        }
        return pre;
    }
}

3.(链表)

解析：使用快慢指针法，定义两个指针，慢指针初始位置为head，快指针初始位置为head.next，设置循环，快指针后移的速度是慢指针的两倍，如果快指针和慢指针相遇，则有环形；如果快指针最终指向null，则没有环形

public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head == null||head.next== null){
            return false;								//判定链表中如果没有元素或只有一个
        }
        ListNode a = head;						//定义慢指针
        ListNode b = head.next;				//定义快指针
        while(a != b){
            if(b == null||b.next == null){
                return false;							//快指针最终指向null，返回false
            }
            a = a.next;								//慢指针速度后移一次
            b = b.next.next;						//快指针后移两次
        }	
        return true;									//快慢指针相遇，循环结束，返回true
    }
}

4.删除链表中的元素（链表）
解析：找一个数据不是val的节点为头结点，定义两个指针指向该节点，一个进行删除操作，另一个进行查找操作，如果查找节点指向要删除的节点，则删除节点直接跳过该节点指向下一个节点

class Solution {
     public ListNode removeElements(ListNode head, int val) {
        while (head != null) {                  //找到一个节点作为头结点
            if (head.val != val)
                break;
            head = head.next;
        }
        ListNode pre = head;                    //删除指针
        ListNode cur = head;                    //查找指针
        while (cur != null) {
            if (cur.val == val){                 
                pre.next = cur.next;            //如果查找到元素，则使删除节点指向该节点的下一个节点
            }else{
                pre = cur;                      //否则使这两个节点指向同一个节点
            }
            cur = cur.next;                     //查找节点后移查找
        }
        return head;
    }
}

5.链表的中间节点（链表）

解析：我们可以将链表转换为一个数组，然后中间节点就是【length/2】

class Solution {
    public ListNode middleNode(ListNode head) {
        ListNode [] arr = new LisNode(100);						//创建一个长度为100的存储节点的数组
        int i = 0;
        while (head.next != null){
        	arr[i++] = head;
        	head = head.next;											//遍历链表存在数组中
        }
        return arr[i/2];														//返回数组的中间元素
    }
}

6.反转二维数组（数组）

解析：可以将每行数组从后往前遍历，然后用1减去每个元素，再返回

class Solution {
    public int[][] flipAndInvertImage(int[][] A) {
        int x=A.length;
        int y=A[0].length;
        int[][] B = new int[x][y];
        for (int i=0;i

7.高度检查器（数组）

解析：可以将原数组先复制一份出来，然后将新数组按升序排好序，最后将原数组与新数组进行比较，得出元素不同的个数

class Solution {
    public int heightChecker(int[] heights) {
        int[] arr = heights.clone();                //将原数组复制一份
        int temp;
        for(int i=0;iarr[j]){
                 temp=arr[i];
                 arr[i]=arr[j];
                 arr[j]=temp;
                }
            }
        }
        int diff = 0;
        for (int i=0; i

8.二叉搜索树的范围和（二叉树）

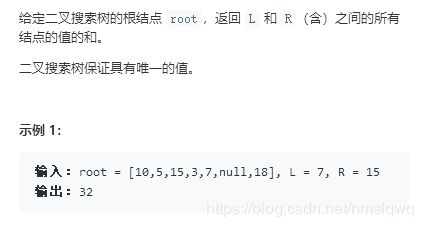
解析：题目要求求出范围在L和R之间的所有元素之和，我们需要对树进行深度优先遍历，从根节点开始，如果节点元素在L和R之间，则进行自加操作，如果元素大于L，则向右子树进行搜索，如果节点元素小于R，则向左子树进行搜索，当节点为null时递归结束

class Solution {
    int sum = 0;				//定义和默认值为0
    public int rangeSumBST(TreeNode root, int L, int R) {
        add(root,L,R);	
        return sum;
    }
    
    public void add(TreeNode p,int L,int R){
        if(p != null){
            if(p.val>=L&&p.val<=R){
                sum += p.val;
            }if(p.val>L){
                add(p.left,L,R);
            }if(p.val<R){
                add(p.right,L,R);
            }
        }
    }
}

9.反转二叉树（二叉树）

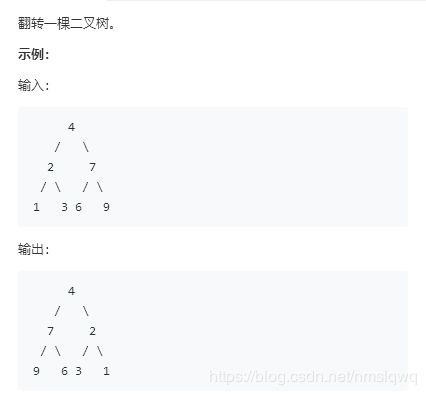
解析：使用递归将每个节点的孩子节点直接互换，最后返回

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return root;
        }
        TreeNode right = invertTree(root.right);
        TreeNode left = invertTree(root.left);
        root.left = right;
        root.right = left;
        return root;
    }
}

10.从二叉搜索树到更大和树（二叉树）

解析：题目要将每个节点的数据改为该节点元素加上所有大于该元素的和，由二叉搜索树的性质可知，节点右边的所有元素都大于该节点元素，所以使用反转的中序遍历将节点右边元素相加重新赋值给该节点即可

class Solution {
    public TreeNode bstToGst(TreeNode root) {
        dfs(root);
        return root;
    }
    
    int sum = 0;// 记录每个节点的右边的所有节点和，即原树中大于 node.val 的值之和
    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        
        dfs(root.right);// 先访问所有大于root的节点
        root.val += sum;// 赋值给当前节点
        sum = root.val;// 保存更大和
        dfs(root.left);// 后访问小于root的节点
    }
}

11.对称二叉树（二叉搜索树）

解析：当一个树二叉树左子树的根节点元素等于右子树的根节点元素，并且每个子树的右子树都与另一个树的左子树对称，则这个二叉树对称

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return add(root,root);
    }
    
    public boolean add(TreeNode t1,TreeNode t2){
        if(t1==null&&t2==null){
            return true;
        }
        if(t1==null||t2==null){
            return  false;
        }
        return (t1.val==t2.val&&add(t1.right,t2.left)&&add(t1.left,t2.right));
    }
}