猪施主

算法笔记——左神初级（8）哈希表、布隆过滤器、一致性哈希、并查集、岛问题

题目1：认识哈希函数和哈希表

哈希表中元素是由哈希函数确定的。

将数据元素的关键字K作为自变量，通过一定的函数关系（称为哈希函数），计算出的值，即为该元素的存储地址。

哈希函数

经典的哈希函数的输入域是无穷大的，接受的参数可以是string类型，返回一个16位的16个值范围的数。
哈希函数的输出域是有穷尽的，虽然很大，但是是个固定的数值
当输入参数固定的情况下，得到的输出值是固定的，它不是随机函数，样本固定得到的输出值也是固定的。
输入不一样，也有可能得到相同的输出值（哈希碰撞，因为输入比输出域大）
虽然会有两个输入对应相同的一个输出，但是对于大量的输入，对应的输出在输出域上是均匀分布的。

注意：对于哈希函数来说，有规律的输入并不能得到有规律的输入，例如十个1Mb的字符串，只有最后1byte的内容不一样，在经过哈希函数后得到的返回值会千差万别，而不会有规律，所以它可以来打乱输入规律。

通常哈希函数的输出域都很大，例如常见的MD5算法，它的输出域是0到264-1，但是往往我们都会将哈希函数的返回值模上一个较小的数m，让哈希函数的输出域缩减为0到m-1，并且模完后的0到m-1这个域上也是均匀分布的。

推广：对于输入对应的哈希值，使其模M之后的结果同样是均匀分布的。其次，可以通过将一个哈希函数的输出按位截取，如高八位和第八位再线性组合的方式得到新的哈希函数。

因为哈希函数的每一位都是相互独立的

哈希表

哈希表的经典结构

JVM中的哈希表：桶下加单链表，便可以形成哈希表的形式。JVM中存放的是桶加红黑树的形式。如果哈希表中单链表长度太长则进行扩容，重新计算所有的hashcode，然后重新模，形成新的哈希表。

实际在使用过程中，还可以离线扩容。比如说这个哈希表的长度是1000，在用的时候发现某条链上的长度为5了，长度为5并不影响使用，增删改查还是O(1)，只是再往上加的时候它的效率快不行了，但是你在get或put时还让你使用原来的结构，于此同时，我在后台给你分配一个更大的区域，比如容量为3000。一个数据经过哈希函数算完后，拿到新结构里放，如果用户有put行为，就同步往新老结构上塞，用户使用get时，从老结构上拿，也就是说不让使用者等待。当后台彻底扩容完成后，用户再用的时候，就把请求切换到新的结构上，然后把老结构销毁，这就是离线扩容。

因为有这么多的优化技巧，所以我们说哈希表的增删改查是O(1)的。

哈希函数在大数据中的应用

需求：我们有一个10TB的大文件存在分布式文件系统上，存的是100亿行字符串，并且字符串无序排列，现在我们要统计该文件中重复的字符串。

整体思路：利用哈希函数分流，以及哈希表的性质：相同输入导致相同输出，不同输入均匀分布。

假设，我们可以调用100台机器来计算该文件。

那么，现在我们需要怎样通过哈希函数来统计重复字符串呢。

首先，我们需要将这一百台机器分别从0-99标好号，然后我们在分布式文件系统中一行行读取文件（多台机器并行读取），通过哈希函数计算hashcode，将计算出的hashcode模以100，根据模出来的值，将该行存入对应的机器中。

根据哈希函数的性质，我们很容易看出，相同的字符串会存入相同的机器中。

然后我们就能并行100台机器，每台机器各自统计有哪些重复的字符串，这样就能大大加加快统计的速度。

如果还嫌单个机器处理的数据过大，可以把机器里的文件再通过哈希函数按照同样的方法把它分成小文件，然后在一台机器中并行多个进程，处理数据。

注意：这10TB文件并不是均分成100GB，分给100台机器，而是将这10TB文件中不同字符串的种类，均分到100台机器中。

题目2：设计RandomPool结构

【题目】设计一种结构，在该结构中有如下三个功能：
insert(key)：将某个key加入到该结构，做到不重复加入。
delete(key)：将原本在结构中的某个key移除。
getRandom()：等概率随机返回结构中的任何一个key。
【要求】 Insert、delete和getRandom方法的时间复杂度都是 O(1)

【思路】：
这个题的结构和哈希表的结构很像，不同的是哈希表是get(key,value)，而这题没有value，只有key，但有getRandom()这个函数。

如果用一张哈希表不能做到等概率随机返回任何一个key，哈希表的结构是，表中的每个位置上都挂一些链，如果样本量很少，必然会出现某一个位置上有数据，其它位置没数据的情况，此时又不能遍历，因为遍历就不是O(1)了；样本量很多的时候，虽然说会均匀分布，每个位置链的长度几乎差不多，但也不是严格一样，所以只用一张哈希表是做不到严格等概率返回一个key的。

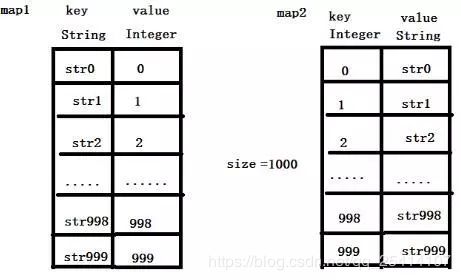
准备两个哈希表，假设A~Z依次进入，哈希表的结构就是：

注意：对应的0-25是指的序号，也就是递增的size！
　　

如果要等概率随机返回一个，可以使用Math.random() * size 随机产生[0,25)中等概率的一个数，随机出哪个数字，就在map2里把该数字对应的字符串返回，这就能做到绝对等概率。

以上是insert(key)和getRandom()的行为。

delete(key)又该怎么做呢？

如果直接在map1和map2中进行删除操作的话，会产生一个个的“洞”，如果0-999这1000个数中，执行了999个删除操作，那么0~999中产生了999个“洞”，只有一个位置上有数据，此时，如果getRandom()的话就会非常慢，这样就不能保证O(1)的时间复杂度。

正确的做法应该是：假设删除了map1中str2上的数据，map2对应的数据也会同步删除，然后把str999放到str2的位置上，再让str2对应的字符串改为999，然后删掉最后一条记录，size变为999。

即产生“洞”的时候，拿最后一个数据“填”这个“洞”，再把最后几个记录删掉，这样就能保证size的index区域还是连续的，此时getRandom()产生的随机数的位置就不会为空了。

注意：value上的0~999这个顺序并不是有序的，因为map本身就是乱序的，我们也不需要value是有序的，我们只要保证map上不存在“洞”，每条记录都是连续的，这样在getRandom()时就不会找不到数。

public class Code_02_RandomPool {

	public static class Pool<K> {
		private HashMap<K, Integer> keyIndexMap;
		private HashMap<Integer, K> indexKeyMap;
		private int size;

		public Pool() {
			this.keyIndexMap = new HashMap<K, Integer>();
			this.indexKeyMap = new HashMap<Integer, K>();
			this.size = 0;
		}

		public void insert(K key) {
			if (!this.keyIndexMap.containsKey(key)) {
				this.keyIndexMap.put(key, this.size);
				this.indexKeyMap.put(this.size++, key);
			}
		}

		public void delete(K key) {
		//先判断是否所要删除的key是否还存在
			if(this.keyIndexMap.containsKey(key)){
				//将key对应的size值读取出来，赋值给deleteIndex
				int deleteIndex = this.keyIndexMap.get(key);
				//将最后的size读取出来
				int lastIndex = --this.size;
				//将最后一个key读取出来
				K lastKey = this.indexKeyMap.get(lastIndex);
				//把最后一条记录"填"到要删除的位置
				//上方的图好好理解，这一步是在左边的表中把k为str999的vlaue改为2
				this.keyIndexMap.put(lastKey, deleteIndex);  
				this.indexKeyMap.put(deleteIndex, lastKey);
				this.keyIndexMap.remove(key);   //删掉最后对应的行
				this.indexKeyMap.remove(lastIndex);  //删掉最后一行，已替换到前面的key去了
			}
		}

		public K getRandom() {
			if (this.size == 0) {
				return null;
			}
			int randomIndex = (int) (Math.random() * this.size); // 0 ~ size -1
			return this.indexKeyMap.get(randomIndex);
		}

	}

题目3：布隆过滤器

主要用来解决查询一个元素是否在一个巨大的集合中的问题，如：黑名单问题，假设有一百亿个url的黑名单，在搜索这些黑名单的时候不想显示，每个url是64个字节，在用户搜索的时候我就需要先过滤。

布隆过滤器会出现虚警率，但不会漏报！

【题目】：如果一个黑名单网站包含100亿个黑名单网页，每个网页最多占64B，设计一个系统，判断当前的URL是否在这个黑名单当中，要求额外空间不超过30GB，允许误差率为万分之一。

实际工程的应用

实际上，布隆过滤器广泛应用于网页黑名单系统、垃圾邮件过滤系统、爬虫网址判重系统等，有人会想，我直接将网页URL存入数据库进行查找不就好了，或者建立一个哈希表进行查找不就OK了。

当数据量小的时候，这么思考是对的，但如果整个网页黑名单系统包含100亿个网页URL，在数据库查找是很费时的，并且如果每个URL空间为64B，那么需要内存为640GB，一般的服务器很难达到这个需求。

那么，在这种内存不够且检索速度慢的情况下，不妨考虑下布隆过滤器，但业务上要可以忍受判断失误率。

位图（bitmap）

布隆过滤器其中重要的实现就是位图的实现，也就是位数组，并且在这个数组中每一个位置只占有1个bit，而每个bit只有0和1两种状态。如上图bitarray所示！bitarray也叫bitmap，大小也就是布隆过滤器的大小。

假设一种有k个哈希函数，且每个哈希函数的输出范围都大于m，接着将输出值对k取余（%m）,就会得到k个[0, m-1]的值，由于每个哈希函数之间相互独立，因此这k个数也相互独立，最后将这k个数对应到bitarray上并标记为1（涂黑）。

等判断时，将输入对象经过这k个哈希函数计算得到k个值，然后判断对应bitarray的k个位置是否都为1（是否标黑），如果有一个不为黑，那么这个输入对象则不在这个集合中，也就不是黑名单了！如果都是黑，那说明在集合中，但有可能会误，由于当输入对象过多，而集合也就是bitarray过小，则会出现大部分为黑的情况，那样就容易发生误判！因此使用布隆过滤器是需要容忍错误率的，即使很低很低！

布隆过滤器重要参数计算

通过上面的描述，我们可以知道，如果输入量过大，而bitarray空间的大小又很小，那么误判率就会上升。那么bitarray空间大小怎么确定呢？不要慌，已经有人通过数据推倒出公式了！！！哈哈，直接用～

假设输入对象个数为n，bitarray大小（也就是布隆过滤器大小）为m，所容忍的误判率p和哈希函数的个数k。计算公式如下：（小数向上取整）

注意：由于我们计算的m和k可能是小数，那么需要经过向上取整，此时需要重新计算误判率p！往往就会更低

可以参考：布隆过滤器原理

假设一个网页黑名单有URL为100亿，每个样本为64B，失误率为0.01%，经过上述公式计算后，需要布隆过滤器大小为25GB，这远远小于使用哈希表的640GB的空间。

并且由于是通过hash进行查找的，所以基本都可以在O(1)的时间完成！

面试过程中可以跟面试官聊，尽可能地去根据要求的规模调整。之后可以多看看大数据相关的题目，带搜索相关的公司基本都会问到。 TAT

题目4：认识一致性哈希

一致性哈希涉及到服务器的负载均衡

传统的服务器抗压策略（负载均衡）

假设，我们有三台缓存服务器，用于缓存图片，我们为这三台缓存服务器编号为0号、1号、2号，现在，有3万张图片需要缓存，我们希望这些图片被均匀的缓存到这3台服务器上，以便它们能够分摊缓存的压力。

【策略】：hash（图片名称）% N

【问题】
问题1：当缓存服务器数量发生变化时，即增减机器时，会引起缓存的雪崩，可能会引起整体系统压力过大而崩溃（大量缓存同一时间失效）。
问题2：当缓存服务器数量发生变化时，几乎所有缓存的位置都会发生改变，怎样才能尽量减少受影响的缓存呢？

一致性哈希

参考这篇博客：zsythink.net/archives/1182/ 以及转载的一篇综合性博客

主要思想是：将哈希值绕成了一个环，然后将服务器结合虚拟节点思想放入环中，去争夺所管理的哈希值，均分整个环。不管加机器或者减少机器都是均分，极大减少了增减机器时的缓存位置改变，不需要全部重复计算。

题目5：认识并查集

并查集有两个功能：

将两个集合中的元素判断是否在同一个集合中，
根据两个集合中的元素将不是同一集合的整和到一起。

实现步骤：

最开始需要将所有的样本点给出
首先第一步将所有各自的数目整成一个集合（每个节点单独形成一个集合）
在一个集合中每个节点都是自己集合中的代表节点，当集合合并的时候，如果决定将2挂到1的底下，此时2所在集合中，只有1节点指向自己，所以1为这个集合的代表节点。
由于每一个集合中都有一个集合的代表节点，所以可以通过代表节点来进行是否在同一个集合的判断，也可以将另外一个集合的代表节点连接到本集合中，此时整个集合也只有一个代表节点，实现集合的整合。（首先进行元素数目的判断，将少元素的集合挂到多元素的底下）
在判断两个是否在同一个集合操作时，在向上查找的过程中，将路径上的所有元素直接连接到代表节点上。

代码如下：

public static class UnionFindSet{
	public HashMap<Node,Node> fatherMap;//第一个Node代表子节点，后面代表父节点
	//key：child   value：father   在查找过程中，就通过fatherMap向上找
	
	public HashMap<Node,Integer> sizeMap;//后面数值代表整个集合中节点的数目
	//其实只有代表节点的size才有意义，在同一个集合内，size都是相等的

	public UnionFindSet(){ //构造函数
		fatherMap = new HashMap<Node,Node>();
		sizeMap = new HashMap<Node,Integer>();
	}
	//初始化操作
	public void makeSets(List<Node> nodes){
		fatherMap.clear();
		sizeMap.clear();
		for(Node node:nodes){	
		//一开始每一个节点单独构成一个集合
			fatherMap.put(node,node);
			sizeMap.put(node,1);
		}
	}
	
	private Node findHead(Node node){  //找头也就是代表节点  递归
		Node father = fatherMap.get(node);
		if(father != node){
			father = findHead(father);
		}
		fatherMap.put(node,father);  //把节点拉扁平
		return father;
	}

	public boolean isSameSet(Node a,Node b){  //判断是否在同一集合
		return findHead(a) == findHead(b);
	}

	public void union(Node a,Node b){  //把两个集合合成一个
		if(a == null || b = null){
			return;
		}
		Node aHead = findHead(a);
		Node bHead = findHead(b);
		if(aHead != bHead){
			int aSetSize = sizeMap.get(aHead);
			int bSetSize = sizeMap.get(bHead);
			//进行判断，如果长度不同，则将短的集合连接到长集合的上面，同时将整体集合的长度相加作为新集合的总长度
			if(aSetSize <= bSetSize){
				fatherMap.put(aHead,bHead);
				sizeMap.put(bHead,aSetSize +bSetSize);
			}else{
				fatherMap.put(bHead,aHead);
				sizeMap.put(aHead,aSetSize+bSetSize);
			}
		}
	}
}

【结论】如果查询次数+合并的次数达到O（N）及以上

那么就应该使用并查集结构来做，这样查询过程的时间复杂度就是O（1）。

题目6：岛问题

【思路】两个for循环，一个for循环是遍历矩阵，遇到0和2就跳过，遇到1进入内层for循环的“感染”过程；“感染”for循环的操作是，将所有和进入位置1沾边的1全部感染成2，同时，岛数++；