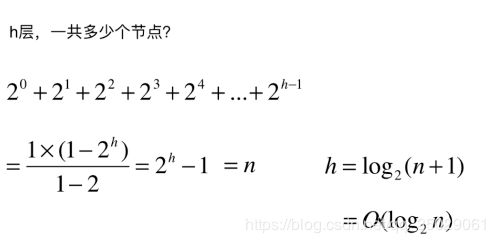java数据结构导图
java数据结构导图
数据结构思维图
线性数据结构
-数组
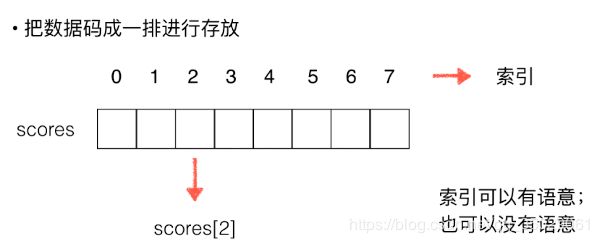
数组的概念就是把数据码成一排进行存放,数组中存放的元素类型必须一。
因为数组中的元素都是一个一个挨着排放的,所以可以给数组中的元素进行编号,从0开始的。
数组只是代存放元素的空间,数组的容量为N,最后的元素的索引为N-1,可以非常快速的直接访问第i个元素是谁。
-队列
是一种线性表
优先队列的底层是堆,不是线性结构,只能从一端添加元素,从另一端取出元素。
与生活中的排队的队列是一致的,是先进先出的数据结构。
队列分为数组队列与循环队列,数组队列出队是O(n)的复杂度,而循环队列入队和出队的复杂度都是o(1)
-栈
是一种线性表,相比数组栈对应的操作是数组的子集,添加元素只能在一端添加元素,取出元素也只能从同一端取出元素。
想从栈中取出元素(出栈),只能取出栈订的元素,用户只能看到最顶层的数据,看不到其他的元素。
栈是后进先出的数据结构(LIFO)。
栈的应用
撤销操作 CRTL+Z ,撤销操作就是从编辑器拿出栈顶的元素。
程序的调用,计算机使用系统栈记录程序的调用过程,子程序的调用。
A2程序执行到A函数第二行中断了,C程序执行完毕看一下系统栈,栈顶是B2,可以跳回B2的位置继续执行,找到上一次中断的位置。
-链表
真正的动态数据结构,不需要处理固定容量的问题。最简单的动态数据结构,天生具有递归性质。
链表的引用和内存相关。
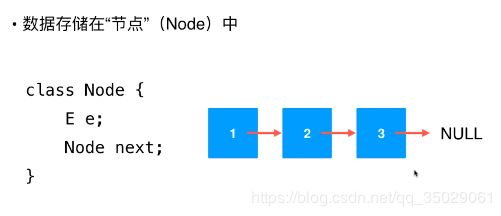
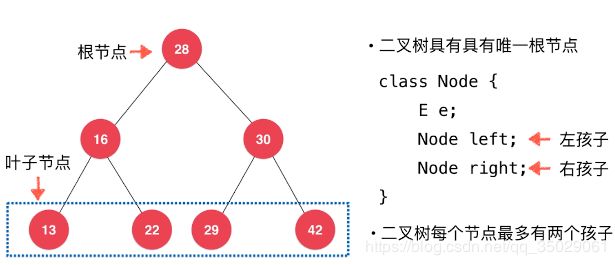
E存储真正的数据,Next是Node类型的数据,也是一个节点,是当前节点的下一个节点,使得数据整合在一起了。
Next为空的节点是最后一个节点。
链表丧失了随机访问的能力,通过索引进行访问。
-哈希表
哈希表的地址空间就是数组,也可以链表与红黑树的复合数据结构(链地址法)
找到关系对应的内容转换为索引用数组进行存储,直接通过索引通过对应关系找到真正关心的内容,数据的复杂度都是o(1)。
键转化为索引的方式就是哈希函数
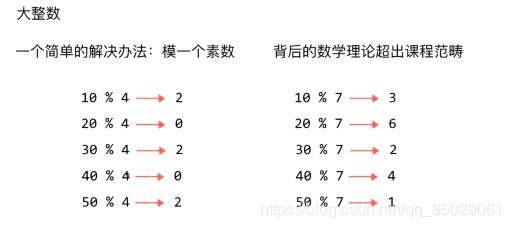
大整数转化索引,取模一个素数,解决分布不均匀的问题
-集合
集合就是承载数据的容器,集合的每个元素只能存在一次,非常快速的完成去重的工作。
抽象数据结构,可分为有序集合与无序集合。
-映射
可以把函数理解为映射,一一映射的关系,一个值向另一个值的对应关系。
映射存储(键与值),数据是一对一对的出现的(Key,Value) ,可以根据键快速的寻找值(Value)
抽象数据结构,分为有序映射(基于搜索树)与无序映射(基于哈希表),多重映射(键可以重复)
树形结构
线性数据结构是将数据排成一排,树形结构下面跟着多个元素
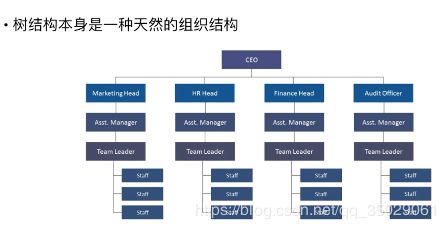
树结构本身是天然的组织结构
使用树结构会更加的高效检索到目标文件,将数据存储为树结构之后,会出奇的高效。
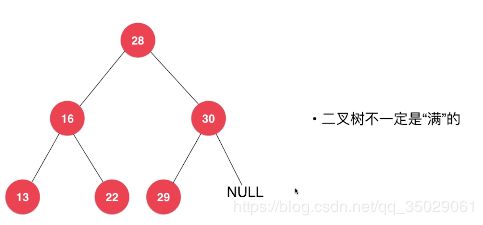
二叉树
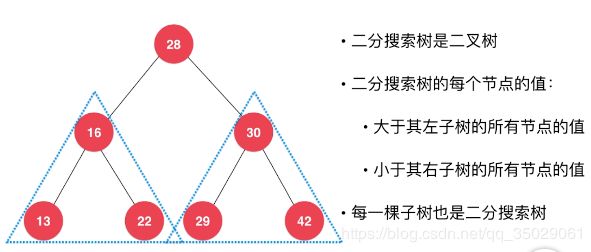
-二分搜索树
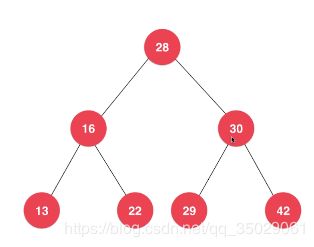
二分搜索树存储的元素必须有可比较性,二分搜索树是有顺序性的,可以获得最大最小值,获得前驱与后继。
二分搜索树的层与节点的关系
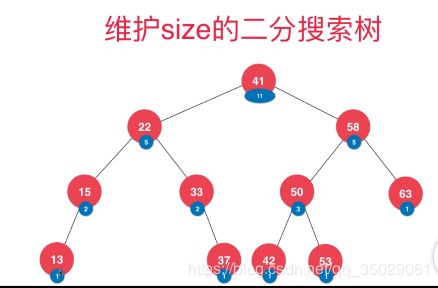
可以对每一个Node维护一个size
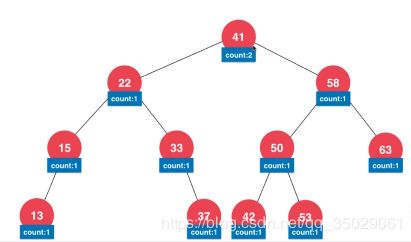
也可以维护深度值
维护元素个数的二分搜索树
-AVL树
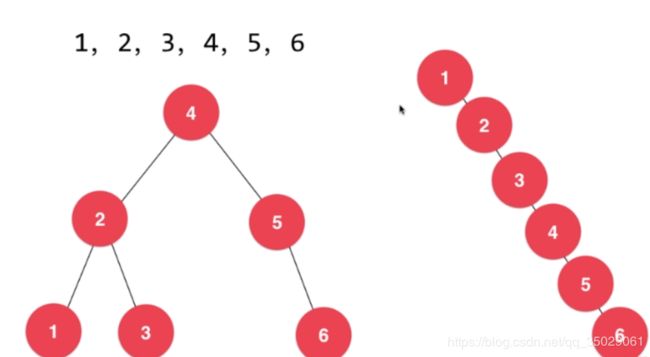
二分搜索树如果是顺序添加进二分搜索树的话,整棵二分搜索树会退化为链表。
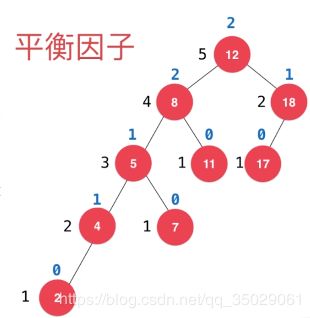
平衡二叉树对于任意一个节点,左子树和右子树的高度值(平衡因子)差不能超过1。
平衡因子左右两颗子树的高度差,8节点的平衡因子为高度3与高度1的差
保留二分搜索树本身性质添加了自平衡(整棵树的高度达到最低的状态,叶子节点最大的深度值和最小的深度值大小不会超过1),
2-3树
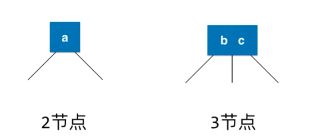
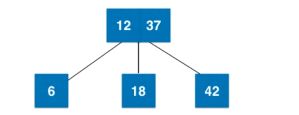
2-3树满足二分搜索树的基本性质,节点可以存放一个元素或者两个元素。
每一个节点有两个孩子或者3个孩子。
满足二分搜索树的性质,左孩子的值小于节点只,右孩子的值大于节点的值。

2-3树是一颗绝对平衡的树,从根节点到任意叶子节点经过的节点数量一定相同。
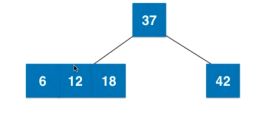
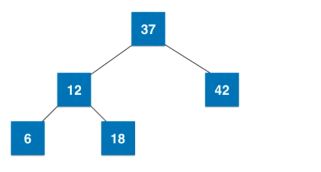
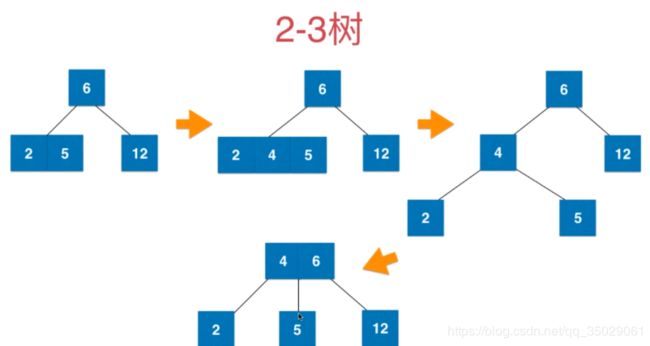
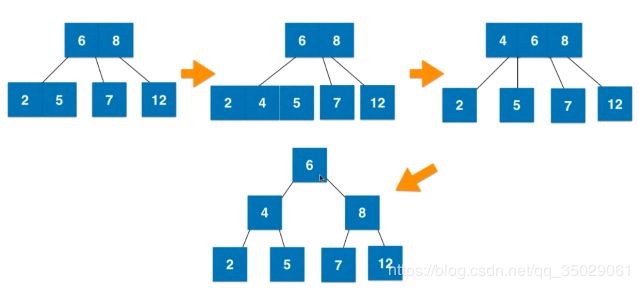
2-3节点的融合与拆解,如果叶子节点是三节点。
叶子节点拆解后如果不是绝对平衡树,新的根节点要与上面的父亲节点融合
融合过程
-红黑树
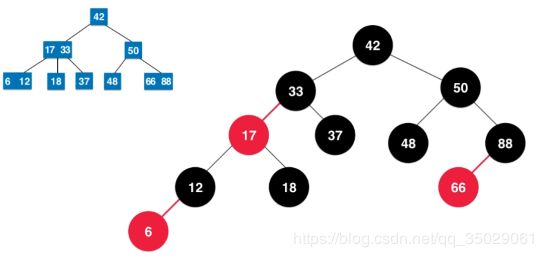
红黑树与2-3树本身是等价的,b与c所在的节点在2-3树中是并列的,为了表示在2-3树中是并列的关系把连接的边标注为红色。
b节点是红色的,b节点与原来的父亲节点在2-3树中是并列的,所有红色节点都是向左倾斜的。
保留二分搜索树本身性质添加了自平衡,相比较AVL树,红黑树统计性能更高,是各种流行的标准库与底层实现的数据结构。
红黑树的性质
空树本身也是红黑树,红黑树严格意义不是平衡二叉树(左右子树的高度差不超过1),但是红黑树保持“黑平衡”的二叉树,左右子树黑色节点的高度差保持着绝对的平衡。
-堆与优先队列
堆是完全二叉树与平衡二叉树(缺失节点的部分叶子节点在整棵树的右下侧,元素按照一层一层的排列顺序排成树的形状),普通的队列是先进先出,堆是优先队列,出队O(logn)顺序和入队O(logn)顺序无关,和优先级有关。
优先队列的应用,操作系统中任务的调度,操作系统回执行多个任务,去动态的选择优先级高的任务执行。
最大堆,堆中任意节点的值总是不大于父亲节点的值。
最小堆,堆中任意节点的值总是大于父亲节点的值。
计算左右孩子的索引
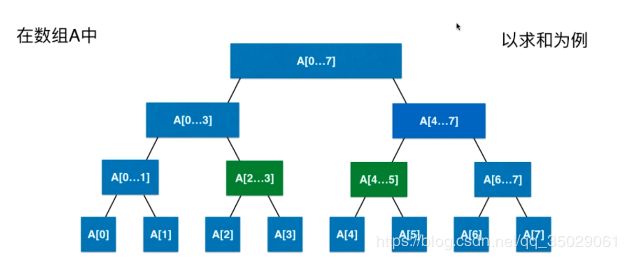
-线段树(区间树)
线段树是二叉树,
以前的数组操作是针对单个元素,现在关心的是一个一个的区间(对一个区间的数据进行更新的同时要进行查询区间的操作),在某一个区间内查询元素。
查询4-7的区间,数据量非常大的话,非常快找到关心的区间对应的一个或多个节点,对区间进行一个或多个操作,不需要对区间的每一个元素都相应的进行遍历。
线段树是平衡二叉树(整棵树最大的深度与最小的深度之间的差最大为1)
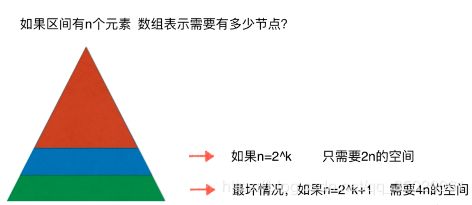
线段树的空间大小
考虑的区间有n个元素的花,线段树需要4n的空间来存储整棵线段树
-Trie(字典树、前缀树)
多叉树,专门为处理字符串设计的数据结构,每一个节点有26个指向下一个节点的指针。next为一个字符到新的节点的映射。
查询任何单词从根节点出发,经过单词有多少个字母,就经过多少个叶子节点。
-并查集
多叉树,孩子节点指向父亲节点形成的数据结构,非常高效的回答连接问题(如网络中的连接状态,人与人之间的关系等)。
存储的数据支持的操作
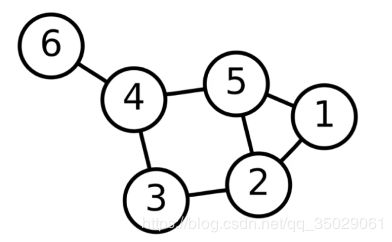
图结构
图研究节点和边构成的数学模型
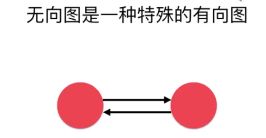
图分为有向图与无向图,有权图与无权图(无向图是一种特殊的有向图,相当于两个有方向的边)
解决的问题,如何获取两点之间的最短路径,如何获得最小生成树,如何遍历整张图,如何获得图中的联通分量,如何获得特殊路径(欧拉路径,哈密尔顿路径),二分图等等
图的连通性
可以是三个图也可以是一个模型中的一张图
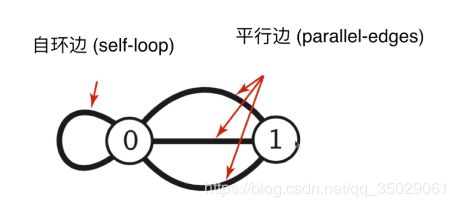
简单图
-邻接表
邻接表适合表示稀疏图,与链地址发的哈希表很像,有N个链表的数组,数组中的每个位置存储的就是与i顶点相连接的其他顶点
每一行只表示和这个顶点相连接的顶点的信息
第一行表示0与1相连
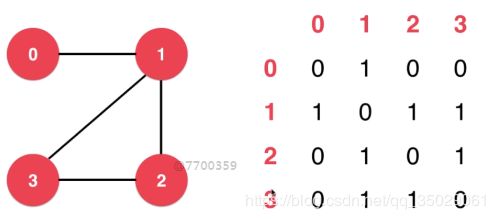
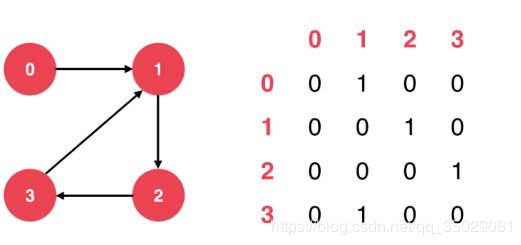
-邻接矩阵
邻接矩阵适合表示稠密图,二维数组中为1对边的表示,1表示相连。
N*N的二维数组,每一行有N个位置来表示一个顶点与图中其他所有顶点边的信息。g[i][j]表示从i到j有一条表,基于斜对角线左右对称