POJ1328Radar Installation(贪心算法)

Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d. 

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates. 

                                                          
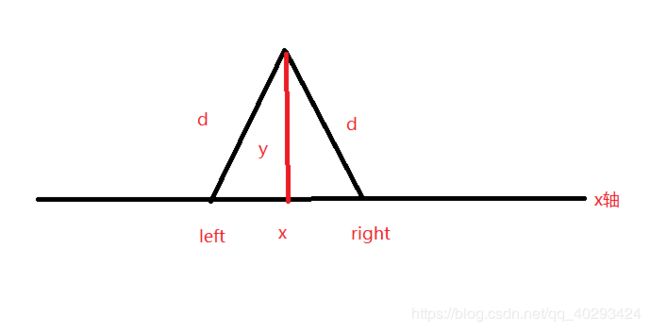
Figure A Sample Input of Radar Installations

 

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases. 

The input is terminated by a line containing pair of zeros 

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.

Sample Input

3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output

Case 1: 2
Case 2: 1

Source

Beijing 2002

 

题目描述： 
假定海岸线是一条无限延伸的直线，陆地在海岸线的一边，大海在另一侧。海中有许多岛屿，每一个小岛我们可以认为是一个点。现在要在海岸线上安装雷达，雷达的覆盖范围是d，也就是说大海中一个小岛能被安装的雷达覆盖，那么它们之间的距离最大为d。 
我们使用平面直角坐标系，定义海岸线是x轴，大海在x轴上方，陆地在下方。给你海中每一个岛屿的坐标位置（x,y）和要安装的雷达所覆盖的范围d，你的任务是写一个程序计算出至少安装多少个雷达能将所有的岛屿覆盖。 
输入描述： 
第一行两个整数n（1≤n≤100000）和d，分别表示海中岛屿的数目和雷达覆盖的范围半径d。 
接下来n行，每行两个整数，表示每个岛屿的坐标位置（x,y）。 
输出描述： 
一行一个整数，即能将所有岛屿全部覆盖至少安装的雷达个数，如果无解则输出“-1”。 

样例输入
3 2
1 2
-3 1
2 1

1 2
0 2

0 0
样例输出
Case 1: 2
Case 2: 1
 
数据范围及提示： 
（1≤n≤100000） 
注意会输出-1 
 

第一步：先行求出以每个岛为圆心，雷达扫描范围d为半径，与海岸线相交得出一个区间（left，right），这个区间即是如果雷                   达在这个区间内，必定可以扫描到小岛。

                        

第二步：然后将区间按照left升序排列，并编号1-n.

考察一个区间 i 的起点 xi的时候,要看从 firstNoCovered 到区间i-1 中是否存在某个区间 c ,没有被 xi 覆盖。

如果没有,则先不急于在xi放雷达,接着往下看。

如果有,那么 c 的终点肯定在xi的左边,因此不可能用同一个雷达覆盖 c 和i。即能覆盖c的点,已经不可能覆盖i和i后面的区间了。此时,为了覆盖c,必须放一个雷达了,放在区间 i-1 的起点即可覆盖所有从firstNoCovered到 i-1的区间。因为当初考察 i-1的起点 z时候,并没有发现 z 漏覆盖了从 firstNoCovered 到 i-2 之间的任何一个区间。

第三步：放完雷达后，firstNoCovered =i；

 其实我也不太明白

其实代码的意思如下：

初始状态temp=1号区间的终点，遍历2-n，

如果下一区间的起点大于temp,则必须放置一个雷达（两个区间不接壤或者交叉，则必须加雷达）num++

如果下一区间的起点小于temp{

如果下一区间的终点小于temp,则temp=小终点

（因为上一区间包含下一区间，则能覆盖下一区间的雷达肯定可以覆盖上一区间）

}   

另外还要注意-1的输出{

1.  -1也是算做一种情况

2.  输出-1的情况：纵坐标>d,纵坐标<0,d<0

}

AC代码：

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
class trans{
	double left;
	double right;
	boolean cover;
}
class cmptrans implements Comparator{
	public int compare(trans a,trans b){
		if(a.left>b.left){
			return 1;
		}else if(a.leftb.right) return 1;
			else if(a.right0&&y>=0){
					arr[i]=new trans();
					double left=x-Math.sqrt(d*d-y*y);
					double right=x+Math.sqrt(d*d-y*y);
					arr[i].left=left;
					arr[i].right=right;
					arr[i].cover=false;
				}
				else{
					radix_num=-1;
				}
				
			}
			if(radix_num!=-1){
				Arrays.sort(arr,1,n+1,new cmptrans());
				double temp=arr[1].right;
				for(int i=2;i<=n;i++){
					if(temp