浮点数相关

读了一些 IEEE 754 实现的浮点数运算相关的文章

• IEEE 754 (IEEE 754-2019)
• Floating-point arithmetic
• Significand
• JavaScript 浮点数陷阱及解法
• 基础野：细说浮点数
• 浮点数的深入分析
• What is the difference between quiet NaN and signaling NaN?
• JavaScript 里最大的安全的整数为什么是2的53次方减一？
• How numbers are encoded in JavaScript
• IEEE754规范的舍入方案怎么理解呢？ - 海枫的回答 - 知乎
• ECMA 262
• IEEE 754 浮点数的表示精度探讨
• Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic - Kahan
• What Every Computer Scientist Should Know About Floating-Point Arithmetic
• 你应该知道的浮点数基础知识

写一写读后感 (以下如无特殊说明, 所有表达时中使用的符号均为相应英文的首字母；浮点数也专指二进制浮点数; 所有内容基于 IEEE 754-2019)

名称	radix	Significand bits (包括1位隐含的整数位)	Decimal digits (精度 = lg2^Significand bits)	指数位	固定偏移值	E min	E max
binary16 半精度浮点数	2	1 + 10 = 11	lg2^11 ≈ 3.31	5	2^(5-1) - 1 = 15	-14 = 1 - +15	2^(5-1) - 1 = +15
binary32 单精度浮点数	2	24	7.22	8	127	−126	+127
binary64 双精度浮点数	2	53	15.95	11	1023	−1022	+1023
binary128 四精度浮点数	2	113	34.02	15	16383	−16382	+16383
binary256 八精度浮点数	2	237	71.34	19	262143	-262142	+262143

                     31
                     |
                     | 30    23 22                    0
                     | |      | |                     |
               type -+-+------+-+---------------------+ value
               特殊值 * 00000000 00000000000000000000000 ±0.0
              
min subnormal number * 00000000 00000000000000000000001 ±2^−23 × 2^−126 = ±2−149 ≈ ±1.4×10^-45
max subnormal number * 00000000 11111111111111111111111 ±(1−2^−23) × 2^−126 ≈ ±1.18×10^-38

   min normal number * 00000001 00000000000000000000000 ±2^−126 ≈ ±1.18×10^-38
                ±1.0 * 01111111 00000000000000000000000 ±1.0
   max normal number * 11111110 11111111111111111111111 ±(2−2^-23) × 2^127 ≈ ±3.4×10^38
 
               特殊值 * 11111111 00000000000000000000000 ±∞
               特殊值 0 11111111 10000000000000000000000 qNaN
               特殊值 0 11111111 01000000000000000000000 sNaN
                -----+-+------+-+---------------------+
                     | |      | |                     |
                     | +------+-+---------------------+
                     |    |    |           |
                     |    |    v           |
                     |    |the implicit bit|
                     |    v                v
                     | exponent         fraction
                     v 
                    sign

32 位单精度浮点数

浮点数存储结构由三部分组成

1. s符号位 sign
   • 0 为正
   • 1 为负
2. e指数位 exponent
   • 指数位 (偏移指数, 也称阶码) 使用无符号整数表示, 范围: [0, 2^e - 1] (偏移指数 = 实际指数 + 固定偏移值. 固定偏移值 = 2^(e-1) - 1)

     1. 偏移指数: 0 表示非规约形式的浮点数或特殊值 ±0

        1. 如果尾数的小数部分非 0, 表示非规约的浮点数
        2. 如果尾数的小数部分是 0, 表示特殊值 ±0 (和符号位相关)

     2. 偏移指数: (0, 2^(e-1) - 1) 表示负指数

     3. 偏移指数: 2^(e-1) - 1 表示 ±0 指数

     4. 偏移指数: (2^(e-1) - 1, 2^e - 1) 表示正指数

     5. 偏移指数: 2^e - 1 表示特殊值 ±∞ 或 特殊值NaN

        1. 如果尾数的小数部分是 0, 表示特殊值 ±∞ (和符号位相关)
        2. 如果尾数的小数部分非 0, 表示特殊值 NaN
           • qNaN (quiet NaN) 尾数的小数部分最高位为 1
             • 将该最高位更改为 0 时, 可能得到特殊值 ±∞ (和符号位相关)
           • sNaN (signaling NaN) 尾数的小数部分最高位为 0
             • 将该最高位更改为 1 时, 得到 qNaN
           • 通常 qNaN 用于使运算正常进行, sNaN 用于引发异常 (是否引发异常取决于 floating-point unit FPU 的状态), 具体见 qNaN 与 sNaN 的区别
   • 使用偏移指数的优点: 可以用长度为 e 个单位的无符号整数来表示所有的实际指数, 这使得两个浮点数的指数大小的比较更为容易
3. m尾数位 mantissa / 有效数 significand (significand 也被叫做 mantissa, 它等于 the implicit bit + fraction)
   • 规约与非规约浮点数
     • 偏移指数: (0, 2^e - 1), 也即 [1, 2^e - 2], 表示规约形式的浮点数. 规约形式的浮点数隐含整数位为 1
     • 偏移指数为 0 且尾数的小数部分非 0, 表示非规约形式的浮点数. 非规约形式的浮点数隐含整数位为 0
     • 非规约形式的浮点数的偏移指数比规约形式的浮点数的偏移指数小 1
       • 例如: 最小规约形式的单精度 (32位 = 1s + 8e + 23f) 浮点数的偏移指数为 1: (-126 + 127), 实际指数为 -126; 而非规约的单精度浮点数的偏移指数为 0: (-126 + 127 - 1), 对应的实际指数也是 -126 而不是 -127
   • 使用隐含整数位的优点: 增加了 1 位浮点数的有效数长度
   • 使用非规约形式的浮点数的优点 (渐进式下溢出 gradual underflow 的优点): 避免了突然式下溢出 abrupt underflow, 使得每个浮点数之间的距离 gap 一致 = 2^(-f + (1 - (2^(e-1) - 1)))

浮点数的特点

• 只能精确表示可由二进制科学计数法 (-1)^s*m*2^e 表示的数值, m 超出精度的部分自动进一舍零

  这也是 0.1, 1.1 等浮点数无法被精确存储的原因

  // 以下使用 JavaScript 实现的双精度浮点数, 精度为 15.95, 约 16 位有效数字
  有效数字是指在一个数中，从该数的第一个非零数字算起的所有数字的长度
  
  (0.1).toPrecision(16);  // "0.1000000000000000" 对于0.1, 有效数为16位
  (0.1).toPrecision(17);  // "0.10000000000000001" 对于0.1, 有效数为17位
  (0.1).toPrecision(18);  // "0.100000000000000006"
  (0.1).toPrecision(22);  // "0.1000000000000000055511"
  
  (1.1).toPrecision(16);  // "1.100000000000000" 对于1.1, 有效数为16位
  (1.1).toPrecision(17);  // "1.1000000000000001" 对于1.1, 有效数为17位
  (1.1).toPrecision(18);  // "1.10000000000000009"
  (1.1).toPrecision(22);  // "1.100000000000000088818"
  
  1.000000000000001;  // 1.000000000000001 有效位数为16位
  1.0000000000000001;  // 1 第17位的1被舍去了
  

• 规约形式浮点数的最大值: ±(1 + (2^-1 + 2^-2 + ... + 2^-f)) * 2^(2^(e-1) - 1) <=> ±(2 - 2^-f) * 2^(2^(e-1) - 1).

  对于双精度浮点数来说, 其规约最大值为: ±(2- 2^-52) * 2^1023 === ±1.7976931348623157e+308, 1.7976931348623157e+308 也是 JavaScript 中 Number 对象静态属性 MAX_VALUE 的值 (注意它不是一个安全整数), 大于该值即表示 ∞ (Number.MAX_VALUE * 1.000000000000001 === Infinity; Number.MAX_VALUE + 1e+292 === Infinity)

• 非规约形式浮点数的最小值: ±2^(-f + (1 - (2^(e-1) - 1))).

  对于双精度浮点数来说, 其非规约最小值为: ±2^(-52-1022) === ±5e-324, 5e-324 也是 JavaScript 中 Number 对象静态属性 MIN_VALUE 的值, 小于该值即表示 0

• 浮点数的安全整数范围 (安全整数范围指浮点数与整数可以一对一): [-(2^m - 1), 2^m - 1]. 对于双精度浮点数来说, 安全整数为: ±2^53 - 1 === ±9007199254740991, 共有 16 位有效数字. 非安全整数的特点是: 一个浮点数对应多个实数, 如下图所示: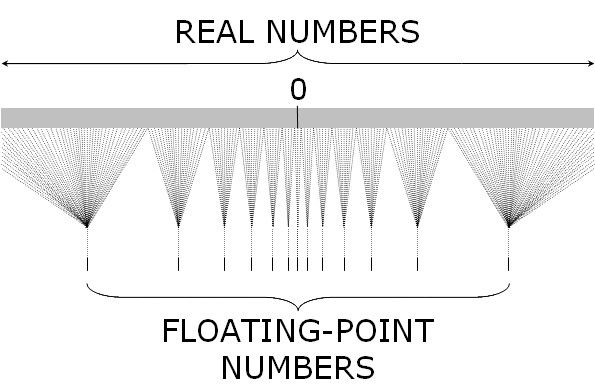

  

  这也是 JavaScript 中 Number 对象静态属性 MAX_SAFE_INTEGER 和 MIN_SAFE_INTEGER 的值

  2^53 + 1 用二进制表示为: 1000...0001 (共 54 位, 两个一分别是 2^53 和 2^0), 转为二进制科学表示法为: 1.000...0001 * 2^53 (尾数的小数部分共 53 位), 由于双精度浮点数的尾数最多能保存 52 位二进制, 因此最后的 1 注定被舍去. 2^53 + 1 与 2^53 存储一致, 也即 2^53 === 2^53 + 1, 2^53 不是一个安全整数

• 浮点数可以准确表示的整数 (除了安全整数范围内的数), 以双精度浮点数为例: 由于尾数的小数部分最多只能存储 52 位, 因此大于浮点数的安全整数范围并且还要精确表示的整数有两类

  • 一类是在指数的范围内增加指数的大小, 且保持尾数始终为 1.0 的数: 2^54, 2^55, 2^56, ..., 2^1023, 这些都是精确的数

  • 另一类是指数与尾数同时更改的数: 对于 [2^53, 2^54) 之间的数, 因为其尾数的小数部分共有 53 位, 第 53 位注定会被舍去, 那我们只要保证数的第 53 位为 0, 那么该数即可精确保证, 也即在 [2^53, 2^54) 之间的偶数才能保证第 53 位为 0, 才能精确表示;

    同理, [2^54, 2^55) 之间的数, 第 53 位和第 54 位注定被舍去, 那我们只要保证数的第 53 位和第 54 位都为 0, 那么该数即可精确保证, 也即在 [2^54, 2^55) 之间, 间距变为 4 的倍数, 这样才能保证第 53 位和第 54 位都为 0, 才能精确表示, 以此类推

浮点数的比较

• 浮点数基本上按照符号位, 指数域, 尾数域的顺序作比较. 显然, 所有正数大于负数; 正负号相同时, 指数的二进制表示法更大的其浮点数值更大; 符号位和指数位相同的, 尾数更大的其浮点数值更大

浮点数的五种舍入方式 (对于二进制浮点数来说是四种舍入方式)

• 舍入到最近的值

  • 舍入到最近的值, roundTiesToEven: 会将结果舍入为最接近且可以表示的值. 如果一样接近, 选择最低有效位为偶数的 (尾数的最低位二进制为 0); 如果最低有效位也相同 (比如 10 进制浮点数 9.5, 9 和 1*e^1 的最低有效位都为奇数), 则选择量级更大的 (对于正数, 越大量级越大; 对于负数, 越小量级越大), 这通常是二进制浮点数的默认舍入方式, 也是十进制浮点数推荐的舍入方式

    // 单精度浮点数(尾数的小数部分23位) Round to nearest, ties to even 示例
    
    // 9.5 表示为二进制科学计数法的浮点数, 舍入一位
    9.5 => 1001.1 => 1.0011 * 2^3
    // 离它最近的两个数分别为 10 和 9
     10 => 1010   => 1.010 * 2^3
      9 => 1001   => 1.001 * 2^3
    // 10 与 9 离 9.5 的距离分别为
    1.010 * 2^3 - 1.0011 * 2^3 = 0.0001 * 2^3  // 0.1
    1.0011 * 2^3 - 1.001 * 2^3 = 0.0001 * 2^3  // 0.1
    // 距离一样接近, 比较其最低有效位
    // 1.010 * 2^3 的最低有效位为 even
    // 1.001 * 2^3 的最低有效位为 odd
    // 因此, 9.5 舍入一位后是 10 而不是 9
    
    // 0.95 表示为二进制科学计数法的浮点数, 舍入一位
    0.95 => 0.11 1100 1100 1100 1100 1100 1
    // 离他最近的两个数分别为 1 和 0.9
       1 => 1.00 0000 0000 0000 0000 0000 0
     0.9 => 0.11 1001 1001 1001 1001 1001 1
    // 1 与 0.9 离 0.95 的距离分别为
    1.00 0000 0000 0000 0000 0000 0 - 0.11 1100 1100 1100 1100 1100 1 = 0.00 0011 0011 0011 0011 0011 1
    0.11 1100 1100 1100 1100 1100 1 - 0.11 1001 1001 1001 1001 1001 1 = 0.00 0011 0011 0011 0011 0011 0
    
    0.00 0011 0011 0011 0011 0011 1 > 0.00 0011 0011 0011 0011 0011 0
    // 0.9 离 0.95 更近一点, 因此 0.95 舍入一位后是 0.9 而不是 1
    

  • 舍入到最近的值, roundTiesToAway: 会将结果舍入为最接近且可以表示的值. 如果一样接近, 选择量级更大的 (对于正数, 越大量级越大; 对于负数, 越小量级越大), 二进制浮点数不需要该舍入方式, 而十进制浮点数应该提供该舍入方式供用户选择

• 定向舍入

  • 朝 +∞ 方向舍入, roundTowardPositive, 也称为向上取整 ceil: 会将结果朝正无穷大的方向舍入
  • 朝 -∞ 方向舍入, roundTowardNegative, 也称为向下取整 floor: 会将结果朝负无穷大的方向舍入
  • 朝 0 方向舍入, roundTowardZero, 也称为截断 truncation: 会将结果朝 0 的方向舍入

• JavaScript 中 Math.round(x) 静态方法的舍入方式

  • 返回最接近 x 的整数. 如果两个整数相等的接近, 那么返回更接近 +∞ 的; 如果已经是整数了, 那么返回它自身

二进制浮点数的异常处理

• 无效运算, Invalid operation. 数学上未定义的运算, 例如 0/0, sqrt(-1.0) 等, 默认返回 qNaN
• 被零除, Division by zero. 除数为零，被除数为有限的非零数字, 默认返回 ±∞
• 上溢, Overflow. 运算产生的结果超出指数能表达的范围 E max, 默认返回 ±∞
• 下溢, Underflow. 运算产生的结果超出了规约浮点数 normal numbers 的范围, 默认返回非规约浮点数 subnormal numbers 或 0 (遵循舍入规则)
• 不精确, Inexact. 运算产生的结果无法精确表示, 默认返回精确结果的舍入值 (遵循舍入规则)

在线转换 (二进制与十进制) 浮点数的链接

• IEEE-754 Floating Point Converter - Single precision 32-bit
• IEEE754 Single precision 32-bit
• IEEE754 Double precision 64-bit

点 ---> IEEE 754-2019 <--- 下载标准