HDU 5296 Annoying problem（LCA模板+树的dfs序心得）

Problem Description

Coco has a tree, whose nodes are conveniently labeled by 1,2,…,n, which has n-1 edge，each edge has a weight. An existing set S is initially empty.
Now there are two kinds of operation:

1 x： If the node x is not in the set S, add node x to the set S
2 x： If the node x is in the set S,delete node x from the set S

Now there is a annoying problem: In order to select a set of edges from tree after each operation which makes any two nodes in set S connected. What is the minimum of the sum of the selected edges’ weight ?

 

Input

one integer number T is described in the first line represents the group number of testcases.( T<=10 ) 
For each test:
The first line has 2 integer number n,q(0 The following n-1 lines each line has 3 integer number u,v,w describe that between node u and node v has an edge weight w.(1<=u,v<=n,1<=w<=100)
The following q lines each line has 2 integer number x,y describe one operation.（x=1 or 2,1<=y<=n）

 

Output

Each testcase outputs a line of "Case #x:" , x starts from 1.
The next q line represents the answer to each operation.

 

Sample Input

1 6 5 1 2 2 1 5 2 5 6 2 2 4 2 2 3 2 1 5 1 3 1 4 1 2 2 5

 

Sample Output

Case #1: 0 6 8 8 4

 

Author

FZUACM

 

Source

2015 Multi-University Training Contest 1

 

题意：

给出一个树(满足n个点，n-1条边)，还有一个原本为空集的点集S，有两种操作：

操作1：向集合S中加入点x(如果x不在集合里面)

操作2：从集合S中删去点x(如果x在集合里面)

对于每次操作，从树上找一个边集，满足S中任意两点连通，求最小的边集（边权之和最小）

分析：

还记得LCA的入门题（HDU2586）求的是树上任意两点间的最短距离，当时有公式

d(a,b)min = dist[a] + dist[b] - 2*dist[lca(a,b)],其中dist是节点到根节点的距离

这题显然也是LCA的题，但是公式不是很好找，题解是这样说的：

先预处理下dfs序
对于添加点u操作：
每次查找集合中的点与添加点的dfs序比他小的最大的点和比他大的最小点，

假设这两个点为x,y（找不到的话就找字典序最大和最小的两个点，理由下面给出）
每次增加的花费为dis[u] - dis[lca(x,u)] - dis[lca(x,y)];其中dis记得是点到根节点的距离
对于删除点u操作：
每次先把点从集合删除，然后再计算减少花费，计算公式和增加的计算方法一样
根据dfs序选择两个点的理由：
如果集合中可以找到dfs序比操作点大和比操作点小的点，那么变化的费用就相当于
操作点到以这两个点为端点的链的距离，可以用上述公式计算

如果集合中dfs序都比操作点小或者都比操作点大，

那么变化的费用是操作点到以字典序最大和字典序最小的点为端点的链的距离，也可以用上面的公式计算

注意添加点的时候是先计算再添加，删除点是先删除再计算

这里的u说的是dfs序，x,y也是dfs序，其实dfs序只是表示u,x,y之间的关系，真正计算时还是要还原到原树上的节点来计算

所以相比于一般的LCA模板，还需要再开一个数组保存dfs序对应的节点

关于dfs序，之前一直感觉模模糊糊不清不楚的，这次借这题好好理解了一下

先上鶸的LCA模板吧：

struct Node
{
    int u, v, w, next;
};
struct LCA
{
    int dp[2 * N][M];
    bool vis[N];
    int tot, head[N];
    Node e[2*N];
    void AddEdge (int u, int v, int w, int &k)
    {
        e[k].u = u, e[k].v = v, e[k].w = w;
        e[k].next = head[u];
        head[u] = k++;
    }
    int ver[2 * N], d[2 * N], first[N], dis[N];//dis[i]表示节点i距离根节点的距离
    //first[i]表示节点i的dfs序
    //节点编号   深度  点编号位置  距离
    void init()
    {
        mem(head,-1);
        mem(vis,0);
        tot = 0;dis[1] = 0;
    }
    void dfs (int u, int dep)
    {
        vis[u] = 1;
        ver[++tot] = u;
        first[u] = tot;
        d[tot] = dep;
        for (int k = head[u]; k != -1; k = e[k].next)
        {
            if (!vis[e[k].v])
            {
                int v = e[k].v, w = e[k].w;
                dis[v] = dis[u] + w;
                dfs (v, dep + 1);
                ver[++tot] = u;
                d[tot] = dep;
            }
        }
    }
    void ST (int n)
    {
        for (int i = 1; i <= n; ++i) dp[i][0] = i;
        for (int j = 1; (1 << j) <= n; ++j)
        {
            for (int i = 1; i + (1 << j) - 1 <= n; ++i)
            {
                int a = dp[i][j - 1], b = dp[i + (1 << (j - 1) )][j - 1];
                dp[i][j] = d[a] < d[b] ? a : b;
            }
        }
    }
    int RMQ (int l, int r)
    {
        int k = 0;
        while ( (1 << (k + 1) ) <= r - l + 1) k++;
        int a = dp[l][k], b = dp[r - (1 << k) + 1][k];
        return d[a] < d[b] ? a : b;
    }
    int Lca(int u, int v)
    {
        int x = first[u], y = first[v];
        if (x > y) swap (x, y);
        return ver[RMQ (x, y)];
    }
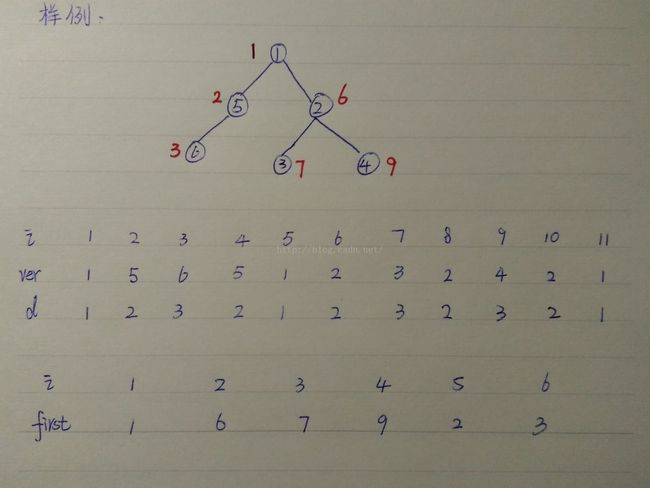
}ans;

画个图帮助理解dfs序：

第一个表，i表示按先序遍历顺序对树的遍历顺序，

ver表示遍历过程中第i次访问的点的编号，d表示遍历过程中第i次访问的点的深度

关键是第二个表，其中first就是鶸模板里面的dfs序，first是怎么来的呢？

其实就是第一个表中每个点第一次被访问对应的i的值，图中红笔标记的就是弱的DFS序了

网上看到有些人的dfs序是从1,2,3,4......这样连续的自然数，不过没关系，我的dfs序离散化之后其实是一样的

dfs序能把非线性的树结构用线性结构保存下来，另外，dfs序一个很重要的性质是：

一颗子树的所有节点在dfs序中是连续的一段

dfs序在树状结构中有很多用法，LCA只是其中一种（文尾贴了dfs序应用的相关资料）

除了dfs序，还有什么bfs序，树剖，LCT什么的（鶸表示暂时还不会。。。）

回到正题。。。。这题。。。。

LCA模板没什么好说的，计算的部分代码中说的很清楚了，上代码：

#define mem(a,x) memset(a,x,sizeof(a))
#include
#include
#include
#include
#include
#include
#include
#include
#include

参考的别人的题解，但是别人的LCA模板和我的不一样，别人的dfs序求出来是从1开始的连续自然数： 点击打开链接

看了看关于DFS序的应用总结：点击打开链接