图论 —— 图的搜索

【概述】

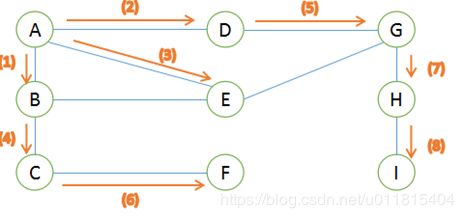
图的搜索问题，是给出一个抽象的字符矩阵代表一张图，根据根据题目要求，对图进行搜索，关于搜索算法：点击这里

根据搜索方法的不同，分为深度优先遍历（DFS）、广度优先遍历（BFS），两者时间复杂度都是 O(N*N)，通常采用深度优先遍历。

【深度优先遍历】

图的深度优先遍历的基本过程为：

1. 从图中某个顶点 v0 出发，首先访问 v0
2. 访问结点 v0 的第一个邻接点，以这个邻接点 vt 作为一个新节点，访问 vt 所有邻接点，直到以 vt 出发的所有节点都被访问
3. 回溯到 v0 的下一个未被访问过的邻接点，以这个邻结点为新节点，重复步骤 2，直到图中所有与 v0 相通的所有节点都被访问
4. 若此时图中仍有未被访问的结点，则另选图中的一个未被访问的顶点作为起始点，重复步骤 1，直到图中的所有节点均被访问

其基本框架为：

int vis[N];
void DFS(int i) {
    for(所有i的邻接点j) {
        if(!vis[j]) {
            if(j == 目标状态)
                return true;
            vis[j]=true;
            dfs(j);
        }
    }
}

【广度优先遍历】

图的广度优先遍历的基本过程为：

1. 从图中某个顶点 v0 出发，首先访问 v0，将 v0 加入队列
2. 将队首元素的未被访问过的邻接点加入队列，访问队首元素并将队首元素出队，直到队列为空
3. 若此时图中仍有未被访问的结点，则另选图中的一个未被访问的顶点作为起始点，重复步骤 1，直到图中的所有节点均被访问过。

其基本框架为：

bool vis[N];
void BFS(int start) {
    queue Q;
    Q.push(start);
    vis[s]=true;
    while(!Q.empty()) {
        int x=Q.front();
        Q.pop();
        if(x==目标状态) {
            ...
        }
        for(所有i的邻接点j) {
            if(!vis[j]) {
                Q.push(j);
                vis[j]=true;
            }
        }
    }
}

【奇偶剪枝】

对于给出的字符矩阵，在搜索过程中，利用奇偶剪枝能极大的降低时间复杂度。

1.内容

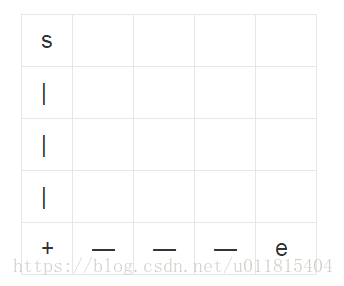
假设起点为（sx,sy），终点为（ex,ey），给定 t 步恰好走到终点，如图所示（“|”竖走，“—”横走，“+”转弯），易证 abs(ex-sx)+abs(ey-sy) 为此问题类中任意情况下，起点到终点的最短步数，记做 step，此处 step1=8；

如图，为一般情况下非最短路径的任意走法举例，step2=14；step2-step1=6，偏移路径为 6

推广：若 t-[abs(ex-sx)+abs(ey-sy)] 结果为奇数，则无法在 t 步恰好到达，返回 false；反之，若结果为偶数，则可以在 t 步恰好到达，返回 true。

2.应用

如图，没障碍物#时，S到E的最短路长为6，但是当有障碍物时，就要绕行了。

如图，黑色为最短路径，当他绕行（红色加蓝色部分）时，其中蓝色部分其实还是最短路径部分平移来的，所以多走的步数也就是红色部分。对于红色部分我们可以分为两部分，一部分是远离最短路径的步数，另一部分是回到最短路径的部分，他们一定是对称的，所以多走的步数一定是偶数。

所以，当问走 x 步能否到达 e，就算出最短路径长 y，如果 x-y 是偶数就能到达，否则不能到达。

【例题】

1.深度优先遍历

1. 红与黑（信息学奥赛一本通-T1216）：点击这里
   同题：Red and Black（HDU-1312）：点击这里
2. 迷宫（洛谷-P1605）：点击这里
3. 迷宫（信息学奥赛一本通-T1215）：点击这里
4. 花生采摘（洛谷-P1086）：点击这里
5. LETTERS（信息学奥赛一本通-T1212）：点击这里
6. 棋盘问题（信息学奥赛一本通-T1217）：点击这里
7. Avoid The Lakes（POJ-3620）：点击这里
8. Cat Snuke and a Voyage（AtCoder-2660）：点击这里
9. Applese 走方格（2019牛客寒假算法基础集训营 Day4-B）：点击这里
10. Pusher（HDU-2821）：点击这里
11. 填涂颜色（洛谷-P1162）：点击这里
12. 01迷宫（洛谷-P1141）(记忆化)：点击这里
13. Tempter of the Bone（HDU-1010）(奇偶剪枝)：点击这里

2.广度优先遍历

1. 仙岛求药（信息学奥赛一本通-T1251）：点击这里
2. 走迷宫（信息学奥赛一本通-T1252）：点击这里
3. 走出迷宫（信息学奥赛一本通-T1254）：点击这里
4. 献给阿尔吉侬的花束（信息学奥赛一本通-T1256）：点击这里
5. 围成面积（信息学奥赛一本通-T1359）：点击这里
6. 迷宫（2019牛客寒假算法基础集训营 Day6-J）：点击这里
7. The Castle（信息学奥赛一本通-T1250）：点击这里
8. Fennec VS. Snuke（AtCoder-2655）：点击这里
9. Rescue（HDU-1242）(终点找起点)：点击这里
10. Catch him（HDU-2351）(块状bfs)：点击这里
11. 迷宫问题（信息学奥赛一本通-T1255）(递归输出)：点击这里
12. Navigating the City（POJ-2435）(通过队列输出)：点击这里
13. Dungeon Master（信息学奥赛一本通-T1248）(三维bfs)：点击这里
14. Applese 走迷宫（2019牛客寒假算法基础集训营 Day4-C）(三维bfs)：点击这里
15. 炫酷迷宫（2019牛客寒假算法基础集训营 Day5-C）(构造+bfs)：点击这里
16. 机器人搬重物（洛谷-P1126）(预处理)：点击这里
17. Lilypad Pondg（POJ-3171）(两次bfs+预处理)：点击这里
18. The Grove（POJ-3182）(射线法)：点击这里
19. Meteor Shower（POJ-3669）(起点的处理)：点击这里