语音 LMS 降噪的 C 语言源代码及其解释

最小均方 (LMS) 算法的自适应数字滤波器原理¹²：

设横向自适应数字滤波器的输入为 $x(n)$，理想输入为 $d(n)$，实际输出为 $y(n)$，滤波器的加权系数为 ${\omega }_i(n),(i=0,1,...,M-1)$，那么 LMS 算法为：

$$\begin{array}{rl}y(n)& =\sum _{i=0}^{M-1}{\omega }_i(n)x(n-i)\\ e(n)& =d(n)-y(n)\\ {\omega }_i(n+1)& ={\omega }_i(n)+2\mu e(n)x(n-i),i=0,1,...,M-1\end{array}$$

其中 $\mu$ 是收敛因子（学习率）。

MATLAB 编程

使用 matlab 对语音进行 LMS 降噪，这样的程序可以找到很多。由于 matlab 在工程方面的应用性能欠佳，最终还是使用 C 语言实现 LMS 的代码更好一些。但是为了对比，我们先写出 matlab 版本的代码，同时对该算法进行说明。

首先我们构造一个正弦信号并给它加上高斯白噪声。输入信号 $x(i)$ 和理想的输出信号 $d(i)$ 分别为：

$$\begin{array}{rl}d(n)& =\sqrt{2}\sin \frac{2\pi i}{20}+v(i)\\ x(i)& =d(i-1)\end{array}$$

其中 $v(i)$ 是均值为零、方差为 1 的高斯白噪声，正弦信号的数字频率为 0.05，信噪比 SNR = 1，$x(i)$ 比 $d(i)$ 延迟一个采样间隔。为什么要这样做呢？有一些代码中，会专门给出一个纯净的信号，并以这个纯净的信号作为参考信号。但是这在现实中是很难获得的。如果你都已经获得纯净信号了，还要滤波有什么意义？所以很多实际应用的程序里面，会将包含噪声的输入信号做延迟，并将延迟后的信号作为输入信号，而原先包含噪声的信号作为纯净信号，一样可以达到自适应滤波的效果。我们这里选取样本数 n=500，滤波器长度 m=20，收敛因子 $\mu =0.0005$。

这个信号我们等会会给出构建程序，现在假定它已经被构造好，保存在了lms.txt文件中。我们就从这个文件里读取。对信号读取并处理的 MATLAB 代码如下：

close all;
clear all; 
clc; 

aaa = textread('lms.txt');             %读取文件
s = aaa(:,2);                          %这个文件中第二列才是真实的信号
s_expand=[s;0];                        %在信号序列最后加一个0
r1=s_expand;
s2 =[0;s];                             %在信号序列最前面加一个0，即把原始信号向后延迟1个点
M=20;                                  % 设置Ｍ和mu，M 是滤波器阶数
mu=0.0005;                             % mu 是自适应滤波里面的参数
itr=length(r1);
[W,e,y2]=LMS(s2,r1,M,mu,itr);
plot(s,'b','LineWidth',1); ylabel('幅值') 
ylim([-3.5 3.5 ]); title('原始语音信号');
hold on;
plot(y2,'r','LineWidth',2); 
ylim([-3.5 3.5 ]); title('LMS滤波输出语音信号');
xlabel('时间/s'); ylabel('幅值')

我们注意到其中使用了 LMS 函数用于滤波的处理，这个函数代码如下：

%LMS函数
function [W,en,y]=LMS(xn,dn,M,mu,itr)
% LMS(Least Mean Squre)算法
% 输入参数:
%     xn   输入的信号序列      (列向量)
%     dn   期望信号           (列向量)
%     M    滤波器的阶数        (标量)
%     mu   收敛因子(步长)      (标量)     要求大于0,小于xn的相关矩阵最大特征值的倒数    
%     itr  迭代次数           (标量)     默认为xn的长度,M<itr<length(xn)
% 输出参数:
%     W    滤波器的权值矩阵     (矩阵)
%          大小为M x itr,
%     en   误差序列(itr x 1)    (列向量)  
%     y    输出序列             (列向量)
% 初始化参数
en = zeros(itr,1);             % 误差序列,en(k)表示第k次迭代时预期输出与实际输入的误差
W  = zeros(M,itr);             % 每一行代表一个加权参量,每一列代表-次迭代,初始为0
% 迭代计算
for k = M:(itr-1)                  % 第k次迭代
    x = xn(k:-1:k-M+1);        % 滤波器M个抽头的输入
    y(k) = W(:,k).' * x;        % 滤波器的输出
    en(k) = dn(k) - y(k) ;        % 第k次迭代的误差
    % 滤波器权值计算的迭代式
    W(:,k+1) = W(:,k) + 2*mu*en(k)*x;
end

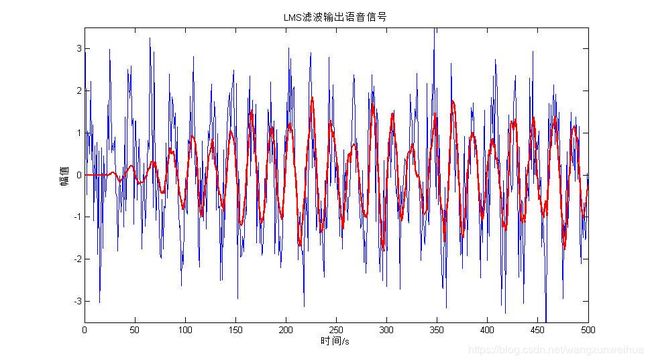
滤波结果画图如下，其中蓝色曲线是滤波之前的，红色曲线是滤波之后的。可以明显看出，滤波以后噪声有所减小。

我们查看输出 y 的数据如下：

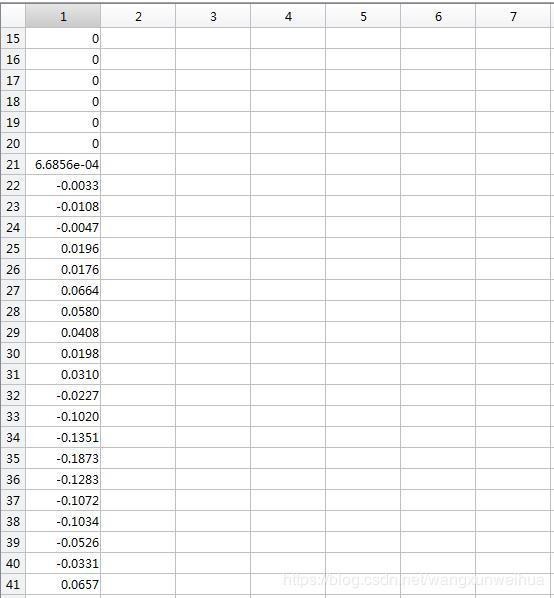
C 语言编程

上面讲解了 MATLAB 的程序，现在来介绍一下对应的 C 语言程序。上面所提到的 lms.txt 这个文件中数据的产生，也包含在本 C 语言程序中。

#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "lms.h"
#include "gauss.h"

int main(void)
{
    int i,m,n;
    long seed;
    double mu,pi,mean,sigma;
    static double d[501],x[501],y[501],w[50];
    FILE *fp;
    pi = 4.0*atan(1.0);
    mean = 0.0;
    sigma = 1.0;
    seed = 13579l;
    n = 500;
    for (i=0;i<n;i++)
    {
        d[i] = sqrt(2.0)*sin(2*pi*i/20.0);
        d[i]+= gauss(mean,sigma,&seed);
    }
    for (i=0;i<(n-1);i++)
    {
        x[i+1]=d[i];
    }
    fp = fopen("lms.txt","w");
    for (i=0;i<n;i++)
    {
        fprintf(fp,"%d %lf\n",i,d[i]);
    }
    fclose(fp);
    m = 20;
    mu = 0.0005;
    lms(x,d,y,n,w,m,mu);
    printf("\n The Coefficients of Adaptive Filter\n");
    for (i=0;i<m;i+=4)
    {
        printf("    %10.7f    %10.7f",w[i],w[i+1]);
        printf("    %10.7f    %10.7f",w[i+2],w[i+3]);
        printf("\n");
    }
    fp = fopen("lmsy.txt","w");
    for (i=0;i<n;i++)
    {
        fprintf(fp,"%d   %lf\n",i,y[i]);
    }
    fclose(fp);
	getchar();
    return 0;
}

我们留意到其中有一个 gauss() 函数，这个函数就是用于产生高斯噪声的，这个函数的源代码如下：

#include "uniform.h"

double gauss(double mean, double sigma, long int* seed)
{
	int i;
	double x, y;
	for (x=0, i=0; i<12; i++)
		x += uniform(0, 1, seed);
	x = x - 6;
	y = mean + x * sigma;
	return (y);
}

我们发现，其中又调用了 uniform 这个函数，这个函数的源代码如下：

double uniform(double a, double b, long int *seed)
{
	double t;
	*seed = 2045 * (*seed) + 1;
	*seed = *seed - (*seed / 1048576) * 1048576;
	t = (*seed) / 1048576.0;
	t = a + (b - a) * t;
	return (t);
}

下面给出 LMS 函数的源代码，这个源代码和 MATLAB 的代码尽可能保持一致， 方便我们进行对比。

void lms(double x[], double d[], double y[], int n, double w[], int m, double mu)
{
    double e[500];
    int i,k;
    for (i=0;i<m;i++)
    {
        w[i] = 0.0;
    }
	/*   //这一段即使不要，也可以自适应滤波
    for (k=0;k
    for (k=(m-1);k<n;k++)  //原始程序里这里就是m，但是改成m-1好像也没问题
    {
        y[k] = 0.0;
        for (i=0;i<m;i++)
        {
            y[k]+=x[k-i]*w[i];
        }
        e[k] = d[k]-y[k];
        for (i=0;i<m;i++)
        {
            w[i]+=2.0*mu*e[k]*x[k-i];
        }
    }

}

C 语言的输出放在 lmsy.txt 这个函数中。我们打开这个文件，看到其中的数据：

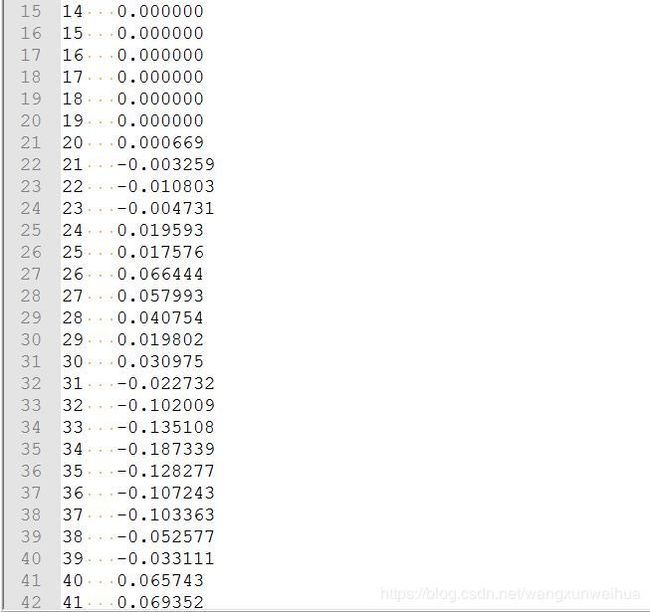
通过逐行对比，我们发现这两种方法的结果是完全一样的，这证明我们的 C 语言程序是正确的。

---

1. 数字信号处理C语言程序集，殷福亮，宋爱军，辽宁科技出版社，1997. ↩︎

2. 语音信号处理实验教程，梁瑞宇，赵力，魏昕，机械工业出版社，2016. ↩︎