运用并查集与最小堆实现Kruskal算法

前言
Kruskal是在一个图（图论）中生成最小生成树的算法之一。（另外还有Prim算法，之后会涉及到）这就牵扯到了最小生成树的概念，其实就是总权值最小的一个连通无回路的子图。（结合下文的示意图不难理解）这里的代码并没有用图的存储结构（如：矩阵，邻接链表等）来处理和运用这个算法，而是最简单的三元组输入，这样会使得这个过程简化很多，至于图的存储方式，在之后总结图数据结构的时候会具体讨论。

Kruskal算法的思想与过程
（1）思想：其实这个算法的本质还是一个贪心算法的过程。其实我们可以这样想，一个图中，我们要想让生成的子图（更确切的说是树）总权值最小，那么只要依次选择图中权值最小的边、权值次小的边、……，这样自然就保证了生成的图总权值最小。但是别忘了一点，我们要求的生成的子图还得是一棵树（树的定义：一个连通无回路的图），这就带来了一个问题，我们在权值从小到大选择边的时候，可能会使生成的子图产生了回路，这就不符合概念了，所以我们不仅需要权值从小到大选择边还应该保证这些边组成的子图构不成回路！这个过程不就是贪心选择的过程吗。

过程（标准定义）：
任给一个有n个顶点的连通网络N = {V, E}，首先构造一个由这n个顶点组成、不含任何边的图T = {V, 空集}，其中每个顶点自成一个连通分量。不断从E中取出权值最小的一条边（若有多条，任取其一），若该边的两个端点来自不同的连通分量，则将此边加入T中。如此重复，直到所有顶点在同一个连通分量上为止。

为何用并查集与最小堆实现Kruskal算法？

这个问题最根本的解答在上面Kruskal算法的实现过程当中，过程中涉及到两个重要的步骤：

(1)每次取得权值最小的边
(2)判断加入的边的两个端点是否来自同一连通分量（实质就是保证加入边后不会产生回路）

而最小堆可以实现每次取得一组数据中关键码（这里可以代表权值大小）最小的数据；并查集可以将不同的集合（这里可以代表点集合）Union起来并且可以判断不同集合是否有交集（这里可以判断两个点是否同属于一个集合，进而判断加入边后是否会出现回路！）。没错！这简直就是Kruskal算法实现的标配，下面Kruskal算法的实现过程图也体现了这一点！（注：之前的博文对最小堆和并查集都有总结，对这两个数据结构概念不清的话可以看看）
Kruskal算法生成最小生成树的一个实例：
程序输入数据（三元组格式）：

7 9 //图的顶点数量、图的边的数量
0 1 28 //下面每行都存储了一个边的信息
0 5 10 //依次表示：边的端点1、边的端点2、边的权值
1 2 16
1 6 14
2 3 12
3 4 22
3 6 18
4 5 25
4 6 24
图表示：

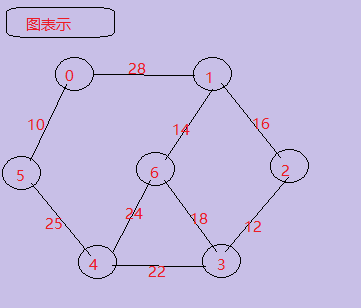
节点中的数字表示节点的序号或者是编号，边上的数字代表每条边的权值，你不要纠结于每条边的权值与其在图上的比例并不协调！因为现实环境中权值的意义有很多，比如花费、代价、重要程度等等。
Kruskal实现过程图解：

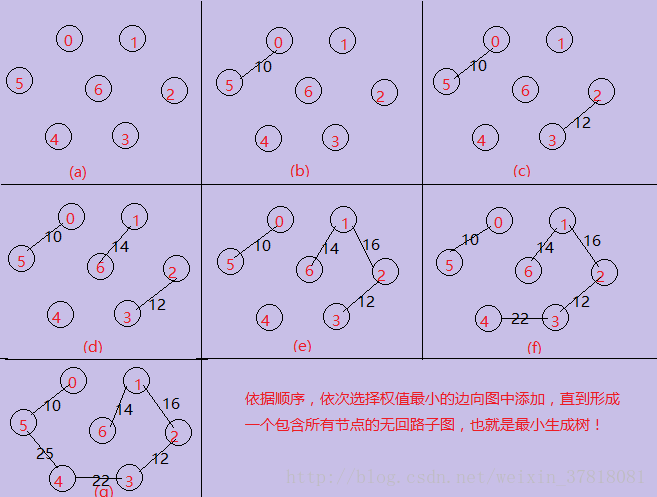
很清晰易懂的图解！

代码实现过程中结构注意点！
（1）对边结构体的构造：

这里必须对此结构变量的大于、大于等于、小于运算符做重载（只通过边的权值比较即可），应为在最小堆中会直接对此变量进行比较！

（2）Kruskal算法实现函数：

尤其注意的应该是并查集建立的时候，其构造函数为何传递了顶点数量多1，否则这会导致一个严重的错误（或者说是隐患）！下面会通过另一个文章着重解释。

（3）关于输出：

这里只是对最小生成树的总权重这个指标进行了输出，其他的指标都可以通过那个保存最小生成树的所有边的全局数组得到。

Kruskal.cpp代码

/*
*运用并查集及最小堆实现Kruskal算法
*/
#include "UFSets.h"
#include "heap.h"
using namespace std;

struct WEDGE {                      //权重边结构定义
    int vertex1, vertex2;           //决定边的两个顶点
    int weights;                    //边的权重
                                    //构造函数
    WEDGE(int v1 = -1, int v2 = -1, int w = 0) {
        vertex1 = v1; 
        vertex2 = v2;
        weights = w;
    }
    bool operator >(WEDGE& WE);     //重载边的大于比较
    bool operator <(WEDGE& WE);     //重载边的小于比较
    bool operator >=(WEDGE& WE);    //重载大于等于比较
};
WEDGE minTreeEdges[20];             //存储最小生成树的边集

void Kruskal(WEDGE* we, int edg_amou, int vex_amou);

int main()
{
    int vertexsAmount{ 0 }, edgesAmount{ 0 };   //输入的点数与边数      
    WEDGE wedge[20];                            //初始化20条边   
    cin >> vertexsAmount >> edgesAmount;
    for (int i = 0; i < edgesAmount; i ++) {    //循环输入边的顶点及权重
        cin >> wedge[i].vertex1 >> wedge[i].vertex2
            >> wedge[i].weights;
    }

    Kruskal(wedge, edgesAmount, vertexsAmount);

    //输出最小生成树的总权重
    int sumWeights{ 0 };
    for (int j = 1; j < vertexsAmount; j ++) {
        sumWeights += minTreeEdges[j].weights;
    }
    cout << sumWeights << endl;

    system("pause");
    return 0;
}

void Kruskal(WEDGE* we, int edg_amou, int vex_amou) {
    //Kruskal算法实现函数，参数分别是：一组边集合、边数、顶点数
    MinHeap minheap(we, edg_amou);       //建立最小堆
    UFSets uf_set(vex_amou + 1);                //建立并查集
    WEDGE edge;
    int vex_1{ 0 }, vex_2{ 0 };
    int count{ 1 };                             //最小生成树加入边数计数
    while (count < vex_amou){                   //选入总边数-1条边即可
        minheap.removeMin(edge);                //删除并返回堆顶元素
        vex_1 = uf_set.Find(edge.vertex1);
        vex_2 = uf_set.Find(edge.vertex2);
        if (vex_1 != vex_2) {                   //两个顶点不在同一连通分量中
            minTreeEdges[count] = edge;         //选入
            uf_set.Union(vex_1, vex_2);         //将两个顶点连通
            count++;
        }
    }
}

//重载运算符定义
bool WEDGE::operator >(WEDGE& WE) {
    if (weights > WE.weights) {
        return true;
    }
    else {
        return false;
    }
}

bool WEDGE::operator<(WEDGE& WE) {
    if (weights < WE.weights) {
        return true;
    }
    else {
        return false;
    }
}

bool WEDGE::operator>=(WEDGE& WE) {
    if (weights >= WE.weights) {
        return true;
    }
    else {
        return false;
    }
}

这个文件中代码的运行需要依靠两个数据结构的头文件——最小堆和并查集.h。这里就不在贴出来了，需要的话可以在文章末的链接下载，也可以看之前对这两个数据结构总结时候所贴的代码。下面用这段代码测试一下我们上面的实例！

嗯，他表现的不错，在我们的过程图中，最终的权值和：10+12+14+16+22+25 = 99。

另类的测试！！！
不过这只是组测试数据，我们应该再找一组程序完全陌生的数据试试，看下面的题目：（题目是在网站中摘下来的~）

数据结构实验之图论六：村村通公路
Time Limit : 1000MS Memory Limit : 65536KB
Submit Statistic
Problem Description
当前农村公路建设正如火如荼的展开，某乡镇政府决定实现村村通公路，工程师现有各个村落之间的原始道路统计数据表，
表中列出了各村之间可以建设公路的若干条道路的成本，你的任务是根据给出的数据表，求使得每个村都有公路连通所需要的最低成本。
Input
连续多组数据输入，每组数据包括村落数目N(N <= 1000)和可供选择的道路数目M(M <= 3000)，随后M行对应M条道路，
每行给出3个正整数，分别是该条道路直接连通的两个村庄的编号和修建该道路的预算成本，村庄从1～N编号。
Output
输出使每个村庄都有公路连通所需要的最低成本，如果输入数据不能使所有村庄畅通，则输出 - 1，表示有些村庄之间没有路连通。
Example Input
5 8
1 2 12
1 3 9
1 4 11
1 5 3
3 2 6
2 4 9
3 4 4
5 4 6
Example Output
19
Author
xam
这是一个典型的应用题，看看下面的测试结果！

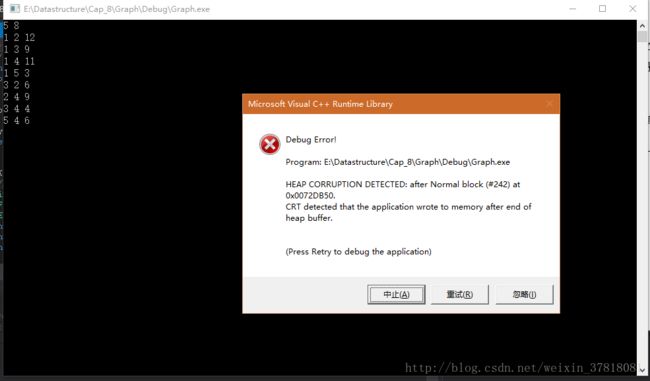
Oh! No!问题似乎很严重！程序崩溃了！这是我们的程序有问题吗？还是其他的bug？也许不是，你可以看看这两组输入数据的微妙差别，也许会受到启发！（其实上文中我已经做了提示）我保证这个Kruskal算法的实现是没有问题的，下篇博文会揭开这一隐患的谜底。

头文件下载链接：
链接：https://pan.baidu.com/s/1eROKT3c 密码：9613