语音增强三，几种固定波束形成技术

Delay and Sum

Fixed Beamforming中最简单的一类——delay and sum，就是信号延迟之后再相加，感兴趣的部分因为信号是相关的，所以越加越大，而不敢兴趣的噪声是不相关的，所以加了和没加一样。这样解释比较通俗一点。稍微不通俗的，Delay and Sum是求解这么一个问题——在约束条件下最大化白噪声增益WNG：

不难得到，此时的滤波器为：

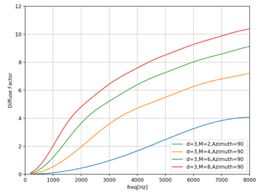
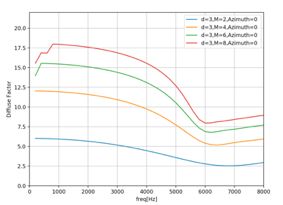
DS最大化WNG的同时（等于10*logM，实际计算WNG和DF的时候要取10*log），Directivity Factor则没有任何的改进（不过后面有专门最大化DF的MaxDF）。比如麦克风个数为8的时候，WNG = 10log8 = 9 ，且是和频率无关的。但是此时的DF仍是和频率、麦克风个数、声源入射角度有关的量。同时，当在高频，扩散声场接近与白噪声场时，DF也会接近WNG的值。下图是我python仿真DF在麦克风距离等于3cm，入射角度为90时候，麦克风个数依次为2、4、6、8时候的Delay and Sum的DF。

 

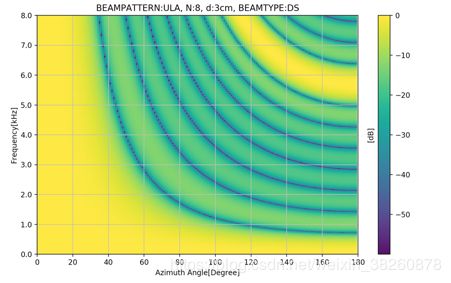
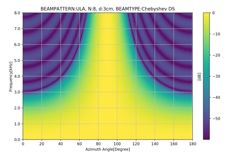
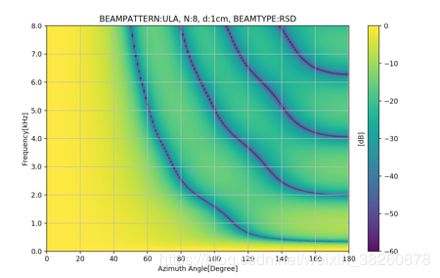
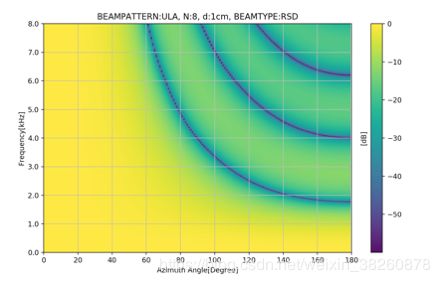
此外，仿真出了Delay and Sum在不同频率下的beampattern的热力图，我们不妨算下，当麦克风间距为3cm时，根据上一章讨论的混叠的条件波长要大于3*2=6cm时才不会发生混叠，也即频率小于5666Hz时不会发生混叠, 下图也明显的可以看到右上方混叠出现的条件，即也是和入射角有关的。 

 

 

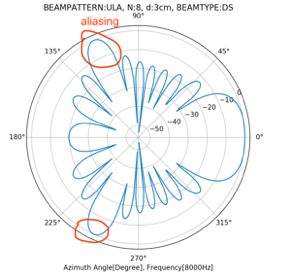
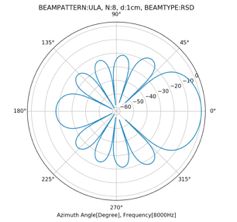
下图则是一个非常明显的混叠的beampattern，阵列响应的旁瓣也同时达到了最大值的。其条件是麦克风个数8，距离3cm，频率8000Hz

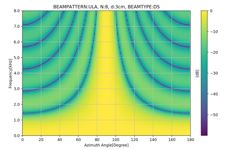
delay and sum的玩法很多，比如可以按照数字信号处理加窗的方法，同样给空间信号加窗，窗的形式也各种各样。比如最典型的一种加Dolph-Chebyshev窗，此方法可以大大降低旁瓣，是一种比较简单的降低旁瓣的技术，但是需要较多数量的麦克风个数。此外。  可以看到下图应用窗之后旁瓣明显降低了许多。

     

---

最大指向性因数 Maximum DF

上述的Delay and Sum（DS）是最大化WNG，而此类则是最大化DF，也即

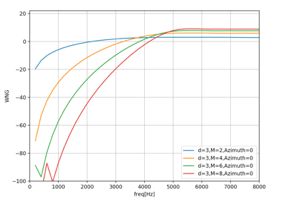
此时对应的阵列的系数即可满足最大化DF，这里就不敲公式了。相比于DS，MDF的DF最大化的同时，肯定损失了WNG，尤其是在低频段，WNG甚至小于0db，反而放大了白噪声。下图就是d=3时，阵列在不同频率及麦克风个数下典型的WNG和DF的表现图。

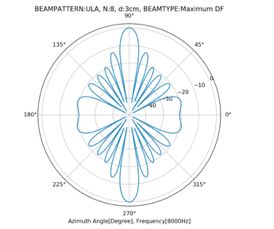
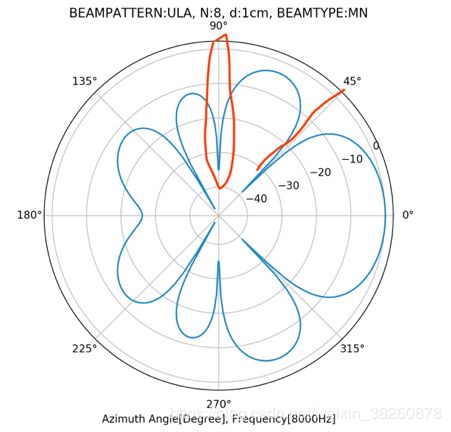
下图则是Maximum在M=8，d=3cm，f=8000，phi=90度时候的beampattern 

数值计算表明，当maxDF的入射角为0或者180的时候，DF才会达到最大。且麦克风间距小的时候，DF也会越来越大。所以我们管这种beamforming叫做superdirective

 

RobustSuperdirective

 

superdirective 的波束形成的DF很漂亮，但是WNG的表现却很糟糕，因此可以给予WNG和DF设置不同的比例因子，进而找到一个能够较好的平衡WNG和DF的beamforming以增加对噪声的鲁棒性，此类的beamforming即为Robust Superdirective。

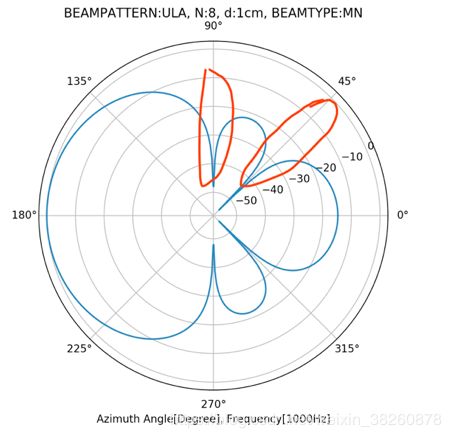
下图分别为平衡因数等于0.01（越大越利于WNG）时候，在f=1000和8000Hz时候beam的表现

      

下两图分别为平衡因数等于0.1和0.9时候阵列的表现。

 

 

Null steering

 

此类波束形成，顾名思义，没有导向矢量（steering vector），只是利用了空间中不同声源的角度，定制化的波束形成。比如有四个声源，角度分别不同，依据此方法，可以只保留第一个声源角度方位信息的信号，而压制其他方位的信号。

同样的此方法涉及到WNG和DF平衡的问题，因此也引入了平衡因数，用以控制这个跷跷板。以下两图分别是45度和90度有干扰声源的null steering（设计0度保持，45、90度压制），可以看到45，90度的信号已经被完全压制，0度时候信号保持的还算可以，但是相应的其他方向比如，90-180度阵列的增益会达到最大。所以应用此方法的前提是只有这几个方向有信号，其他方向都没有。

  

 

subspace法

最后一种则是subspace法，子空间法。

我花了很多的时间研究此方法，但最终还是没能得到正确的结果，很遗憾。

方法的核心思想是把信号分解到只有噪声+信号和只有噪声的子空间中，通过联合对角化的方法求得特征向量及对应的特征值，特征值按降序排列，对应的特征向量对应不同的子空间。求解时只要按序选择不同的子空间个数就可以得到不同的beamforming。当取全部的特征向量时，对应的是Delay and Sum，当取第一个特征值最大对应但特征向量的时候则是super directive。依次来平衡WNG和DF。

我花了很长的时间研究矩阵的联合对角化，从一开始自己看原文理解，到最后求助原文作者提供给我参考书籍获得联合对角化的求解matlab代码，照葫芦画瓢用python实现了一下，但还是没能得到正确结果。此时花费的时间已经约4-5天，有点太长了，所以就停下来继续准备后续的adaptive了。并于今天做了此文的总结。

不过也不是一点收获也没有，我借此重新学习了特征值、特征向量、矩阵对角化等概念，这些在降噪、盲分离中非常重要，但计算开销较大，还好，还好，因此子空间在实时降噪增强中并不多见。于是乎，就先这样吧，以后说不定哪一天就突然拨开乌云见天日了呢。

下一周adaptive beamforming搞起！  

---

更新，不死心的我今天又琢磨了一天的subspace，这一次终于对了。是numpy函数dot一维向量自动计算内积造成的，真的太坑了。。稍微没注意。。搞了好几天。。。真是大坑，不过搞定了问题终于松了一口气，可以开开心心的进击adaptive filter了