计算机仿真——线性规划的MATLAB实现(附例程)
计算机仿真——线性规划的MATLAB实现
线性规划(Linear Programming Problem:LPP)是优化现实生活中遇到的问题。其数学模型常常由目标函数和约束条件组成。目标函数可以使求最大值,也可以是求最小值,约束条件的不等号可以使小于号也可以是大于号。
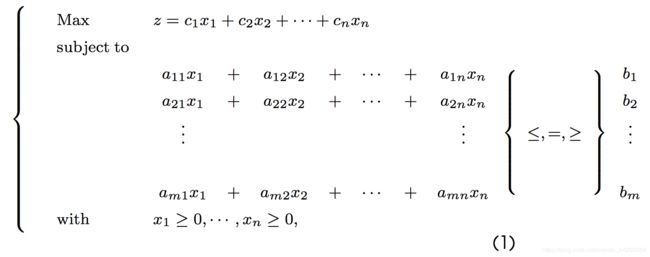
为了避免以上形式多样性带来的不便,Matlab中线性规划的标准模为:

基本函数形式为linprog(c,A,b),它的返回值是向量x的值。还有其它的一些函数调用形式(见附表),如:
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,x0,OPTIONS)
其中fval返回目标函数的值,LB和UB为变量x的下界和上界,x0时x的初始值,OPTIONS是控制参数。
【问题提出】
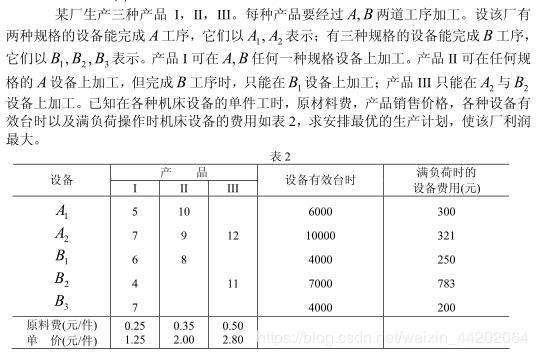
【问题分析】
对产品I来说,设A1、A2完成A工序的产品分别为x1,x2件,转入B工序时,以B1、B2、B3完成B工序的产品分别为x3、x4、x5件;对产品II来说,设A1、A2完成A工序的产品为x6,x7件,转入B工序时,以B1完成B工序的产品为x2件;对产品III来说,设以A2完成A工序的产品为x9件,则以B2完成B工序的产品也为x9件。有由上述条件可得数学模型:

【MATLAB程序】
c=zeros(1,9); %目标函数系数c初始化
s=sym(’(1.25-0.25)(x1+x2)+(2-0.35)x8+(2.8-0.5)x9-(5x1+10x6)/20-321(7x2+9x7+12x9)/10000-250(6x3+8x8)/4000-783*(4x4+11x9)/7000-7x5/200’);
s1=simplify(s); %目标函数化简为标准型
s2=coeffs(s1); %获得目标函数的系数c向量
s3=double(s2); %将符号性矩阵转换为数值型矩阵
c(1)=s3(1);c(2)=s3(2);c(8)=s3(3);c(9)=s3(4);c(6)=s3(5);c(7)=s3(6);c(3)=s3(7);c(4)=s3(8);c(5)=s3(9);
A=[5,0,0,0,0,10,0,0,0;0,7,0,0,0,0,9,0,12;0,0,6,0,0,0,0,8,0;0,0,0,4,0,0,0,0,11;0,0,0,0,7,0,0,0,0]; %约束不等式
b=[6000;10000;4000;7000;4000];
Aeq=[1,1,-1,-1,-1,0,0,0,0;0,0,0,0,0,1,1,-1,0]; %约束方程
beq=[0;0];
x=linprog(-c,A,b,Aeq,beq,zeros(9,1)) %线性规划求解算法,返回最优解对应的x值
fprintf(‘The most profit is Value=%.5f\n’,cx); %求出最优解下的最大利润
【运行结果】
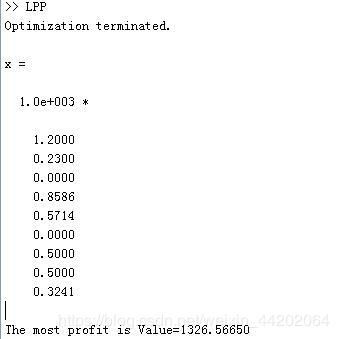
附表
LINPROG Linear programming.
X=LINPROG(f,A,b) attempts to solve the linear programming problem:
min f'*x subject to: A*x <= b
x
X=LINPROG(f,A,b,Aeq,beq) solves the problem above while additionally
satisfying the equality constraints Aeq*x = beq.
X=LINPROG(f,A,b,Aeq,beq,LB,UB) defines a set of lower and upper
bounds on the design variables, X, so that the solution is in
the range LB <= X <= UB. Use empty matrices for LB and UB
if no bounds exist. Set LB(i) = -Inf if X(i) is unbounded below;
set UB(i) = Inf if X(i) is unbounded above.
X=LINPROG(f,A,b,Aeq,beq,LB,UB,X0) sets the starting point to X0. This
option is only available with the active-set algorithm. The default
interior point algorithm will ignore any non-empty starting point.
X=LINPROG(f,A,b,Aeq,beq,LB,UB,X0,OPTIONS) minimizes with the default
optimization parameters replaced by values in the structure OPTIONS, an
argument created with the OPTIMSET function. See OPTIMSET for details.
Options are Display, Diagnostics, TolFun, LargeScale, MaxIter.
Currently, only 'final' and 'off' are valid values for the parameter
Display when LargeScale is 'off' ('iter' is valid when LargeScale is 'on').
[X,FVAL]=LINPROG(f,A,b) returns the value of the objective function at X:
FVAL = f'*X.
[X,FVAL,EXITFLAG] = LINPROG(f,A,b) returns an EXITFLAG that describes the
exit condition of LINPROG. Possible values of EXITFLAG and the corresponding
exit conditions are
1 LINPROG converged to a solution X.
0 Maximum number of iterations reached.
-2 No feasible point found.
-3 Problem is unbounded.
-4 NaN value encountered during execution of algorithm.
-5 Both primal and dual problems are infeasible.
-7 Search direction became too small; no further progress can be made.
[X,FVAL,EXITFLAG,OUTPUT] = LINPROG(f,A,b) returns a structure
OUTPUT with the number of iterations taken in OUTPUT.iterations, the type
of algorithm used in OUTPUT.algorithm, the number of conjugate gradient
iterations (if used) in OUTPUT.cgiterations, and the exit message in
OUTPUT.message.
[X,FVAL,EXITFLAG,OUTPUT,LAMBDA]=LINPROG(f,A,b) returns the set of
Lagrangian multipliers LAMBDA, at the solution: LAMBDA.ineqlin for the
linear inequalities A, LAMBDA.eqlin for the linear equalities Aeq,
LAMBDA.lower for LB, and LAMBDA.upper for UB.
NOTE: the LargeScale (the default) version of LINPROG uses a primal-dual
method. Both the primal problem and the dual problem must be feasible
for convergence. Infeasibility messages of either the primal or dual,
or both, are given as appropriate. The primal problem in standard
form is
min f'*x such that A*x = b, x >= 0.
The dual problem is
max b'*y such that A'*y + s = f, s >= 0.