【数据挖掘】基于密度的聚类方法 - DBSCAN 方法 ( DBSCAN 原理 | DBSCAN 流程 | 可变密度问题 | 链条现象 | OPTICS 算法引入 | 聚类层次 | 族序概念 )
文章目录
- I . DBSCAN 简介
- II . DBSCAN 算法流程
- III . DBSCAN 算法 优缺点
- IV . 可变密度问题
- V . 链条现象
- VI . OPTICS 算法原理
- VII . 聚类分组包含关系
- VIII . 根据层次进行聚类
- IX . 族序 ( Cluster Ordering ) 概念
I . DBSCAN 简介
1 . DBSCAN 算法原理 :
① 聚类条件 : 如果 样本对象 p p p 与 q q q 有密度连接关系 , 那么 p p p 和 q q q 样本就会被分到同一个聚类中 ;
② 噪音识别 : 如果 样本对象 与 其它的样本对象 没有密度连接关系 , 那么该样本就是噪音 ;
2 . DBSCAN 总结 : 一个 聚类 就是 所有 密度相连 的 的 数据样本 的最大集合 , 密度连接所有可以连接的样本 , 组成一个聚类 ;
II . DBSCAN 算法流程
1 . 输入算法参数 : 算法开始时 , 需要输入两个参数 ;
① 参数一 : ε \varepsilon ε 参数 , 是 ε \varepsilon ε-邻域 的 半径 ;
② 参数二 : MinPts 参数 , 是 ε \varepsilon ε-邻域中要求的含有的最低样本个数 , 即阈值 ;
2 . 选择样本 : 随机选择一个数据样本 p p p ;
3 . 判定核心对象 : 判定数据样本 p p p 是否是核心对象 , 通过判定其 ε \varepsilon ε-邻域 中分布的样本数量是否大于等于 MinPts 阈值 个数 , 也就是其中的样本分布达到一定的密度 ;
4 . 如果 p p p 是核心对象 :
① 标记聚类分组 : 当前以 p p p 为中心的 ε \varepsilon ε-邻域 中的所有样本 , 与 p p p 都是直接密度可达的 , 也是密度可达 , 密度连接的 , 因此 ε \varepsilon ε-邻域 中的所有点 , 包括 p p p 点 , 可以划分到同一个聚类分组中 ;
② 搜索所有密度可达样本 : 在上面的聚类分组基础上 , 通过广度优先搜索 , 找到所有的密度可达的样本 , 划分到该聚类分组中 ;
5 . 如果 p p p 是边界对象 ( 非核心对象 ) : 将 p p p 样本标记成噪音 , 再随机地选取另外一个数据样本进行处理 ;
6 . 迭代要求及算法终止条件 : 继续选择样本 , 执行 2.3.4.5.6 2 . 3 . 4. 5.6 2.3.4.5.6 操作 进行迭代 , 直到所有的样本全部被标记完成 ;
III . DBSCAN 算法 优缺点
1 . DBSCAN 算法优点 :
① 算法复杂度 : DBSCAN 算法复杂度是 O ( n ) O(n) O(n) , n n n 代表 数据集样本个数 ;
② 识别模式多 : DBSCAN 算法可以得到任意形状的聚类分组 , 如凹形 , 马蹄形 等 ;
③ 鲁棒性好 : DBSCAN 算法鲁棒性好 , 可以屏蔽异常点 , 噪音 的干扰 ;
④ 不需要设定聚类分组参数 : DBSCAN 算法不需要参数 k k k , 不需要提前指定其聚类分组个数 , 这个参数设置不好 会影响聚类效果 ;
2 . DBSCAN 算法缺点 :
① 需要设置额外参数 : DBSCAN 算法需要设置 ε \varepsilon ε-邻域半径参数 和 MinPts 邻域最小样本阈值 参数 , 这两个参数只是会影响 ;
② 密度可变 : DBSCAN 算法 对于密度可变的数据集进行聚类分析效果很差 , 这里的密度可变指的是 聚类分组 中的样本密度不同 ; 数据集样本中一部分密度大 , 一部分密度小 ;
③ 链条现象 : DBSCAN 算法 存在链条现象 ;
IV . 可变密度问题
1 . 样本描述 : 针对密度可变的数据集样本 , 不同的聚类分组中 , 样本的密度不同 ; 一部分样本密度大 , 一部分样本密度小 ;
示例 : 如 , 聚类 1 1 1 中单位面积内样本有 20个 , 聚类 2 2 2 中单位面积内有样本 4 个 ;
2 . 参数值设定问题 :
① 问题描述 : 这样为其设置 ε \varepsilon ε-邻域半径参数 和 MinPts 邻域最小样本阈值 参数 时 , 就不太好设置 ;
② 半径设置小 : 如果半径设置的小了 , 密度低的聚类 , 可能全部给打散成噪音值 ;
③ 半径设置大 : 如果半径设置的大了 可能整个数据集只有一个聚类 ;
3 . 图示 : 紫色的样本密度很大 , 绿色的样本密度很小 , 此时如果设置 ε \varepsilon ε-邻域半径参数 比较大 , 那么只有一个聚类分组 , 如果设置 ε \varepsilon ε-邻域半径参数比较小 , 绿色的样本就会被标记成异常点 , 当做噪音处理 ;

V . 链条现象
两个聚类分组中 , 出现一个链条 , 少数个别的样本 , 将两个本应该分开的聚类分组 进行了 密度连接 , 导致 两个聚类分组 变成了一个聚类分组 ;
VI . OPTICS 算法原理
OPTICS 算法 原理 :
① 排序索引 : 给所有的 数据样本对象 进行排序 , 并为每个样本对象设置对应的顺序 索引值 ;
② 索引值意义 : 表示样本 基于 密度 的聚类分组 的结构 , 同一个聚类分组的 样本 , 顺序相近 ;
③ 根据索引排列 : 将全体数据集样本数据 , 根据该索引值 , 排列在坐标系中 , 索引值就是 x x x 轴的坐标值 , 排列的结果就是不同层次的聚类分组 ;
VII . 聚类分组包含关系
1 . 聚类分组包含关系 :
① 前提 : 为 数据集样本 进行 聚类分组时 , MinPts 邻域最小样本阈值 参数不变时 ;
② 密度大的聚类 : 当设置的 ε \varepsilon ε-邻域 的 ε \varepsilon ε 半径比较小的时候 , 其聚类的结果为 C 0 C_0 C0 ;
③ 密度小的聚类 : 当设置的 ε \varepsilon ε-邻域 的 ε \varepsilon ε 半径比较大的时候 , 其聚类的结果为 C 1 C_1 C1 ;
④ 包含关系 : C 0 C_0 C0 肯定完全包含在 C 1 C_1 C1 中 ; 密度小的聚类 , 肯定被密度大的聚类包含 ;
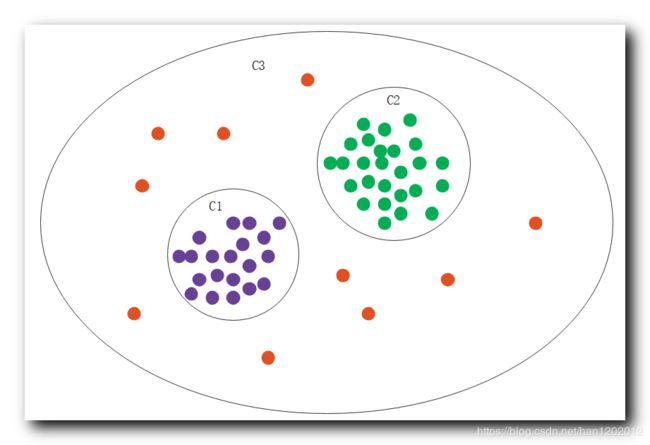
2 . 聚类分组示例 :
当设置比较小的 ε \varepsilon ε 参数时 , 得到的聚类结果是 C 1 C_1 C1 和 C 2 C_2 C2 ;
当设置比较大的 ε \varepsilon ε 参数时 , 得到的聚类结果是 C 3 C_3 C3 ;
由图中可以看出 , C 3 C_3 C3 包含 C 1 C_1 C1 和 C 2 C_2 C2 , 它们之间具有层次关系 , C 3 C_3 C3 可以看做 C 1 C_1 C1 和 C 2 C_2 C2 的父容器 ;
VIII . 根据层次进行聚类
根据层次进行聚类 :
进行聚类分析时 , 将不同层次的 聚类分组 都划分出来 , 也就是使用不同的 ε \varepsilon ε 参数 , 进行聚类分析 , 最终得出不同的聚类分组结果 , 这些结果之间有层次关系 ;
只针对一个 ε \varepsilon ε 参数 进行聚类分组 , 聚类结果很片面 , 效果不佳 ;
IX . 族序 ( Cluster Ordering ) 概念
1 . 族序 ( Cluster Ordering ) 概念 :
① 多层次同时聚类 : 不同层次的聚类分组 , 可以同时进行构建 ;
② 顺序处理样本 : 处理数据集样本对象时 , 使用特定的顺序进行处理 ;
③ 顺序扩展 : 数据集样本对外扩展时 , 按照该顺序进行扩展 ,
④ 族序概念 : 该特定顺序就是 族序 ( Cluster Ordering ) ;
2 . 聚类顺序 : 从 低层 到 高层 ; 从 稠密 到 稀疏 ;
聚类时 , 低层 的聚类分组 要首先构建完成 , 也就是 ε \varepsilon ε 参数 较小的聚类分组 ;
3 . 密度可达的两种情况情况 : 两个样本 密度可达 , 有两种情况 :
① ε \varepsilon ε 参数小 : 一种情况是 ε \varepsilon ε 参数 较小的时候 , 这两个样本就可以密度可达 ;
② ε \varepsilon ε 参数大 : 另一种情况是 ε \varepsilon ε 参数 取值很大时 , 才可以密度可达 ;
4 . 扩展样本优先级 : 扩展样本对象时 , 优先选择第一种情况 , ε \varepsilon ε 参数 较小的时候 就可以密度可达的样本 ;
5 . 每个样本对象需要存储两个值 : 核心距离 与 可达距离 ;