零基础入门深度学习(四):卷积神经网络基础之池化和Relu
![]()
课程名称 | 零基础入门深度学习
授课讲师 | 孙高峰 百度深度学习技术平台部资深研发工程师
授课时间 | 每周二、周四晚20:00-21:00
编辑整理 | 孙高峰
内容来源 | 百度飞桨深度学习集训营
出品平台 | 百度飞桨
01
导读
本课程是百度官方开设的零基础入门深度学习课程,主要面向没有深度学习技术基础或者基础薄弱的同学,帮助大家在深度学习领域实现从0到1+的跨越。从本课程中,你将学习到:
-
深度学习基础知识
-
numpy实现神经网络构建和梯度下降算法
-
计算机视觉领域主要方向的原理、实践
-
自然语言处理领域主要方向的原理、实践
-
个性化推荐算法的原理、实践
本周为开讲第三周,百度深度学习技术平台部资深研发工程师孙高峰,开始讲解深度学习在计算机视觉方向实践应用。今天为大家带来的是卷积神经网络基础之池化和Relu。
02
池化(Pooling)
池化是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出,其好处是当输入数据做出少量平移时,经过池化函数后的大多数输出还能保持不变。比如:当识别一张图像是否是人脸时,我们需要知道人脸左边有一只眼睛,右边也有一只眼睛,而不需要知道眼睛的精确位置,这时候通过约化某一片区域的像素点来得到总体统计特征会显得很有用。由于池化之后特征图会变得更小,如果后面连接的是全连接层,能有效的减小神经元的个数,节省存储空间并提高计算效率。如 图10 所示,将一个的区域池化成一个像素点。通常有两种方法,平均池化和最大池化。
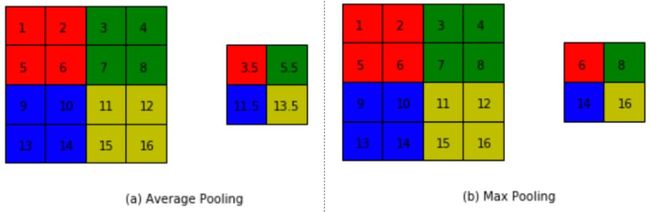
图10:池化
-
如图10(a):平均池化。这里使用大小为的池化窗口,每次移动的步长也为2,对池化窗口内的元素数值取平均,得到相应的输出特征图的像素值。
-
如图10(b):最大池化。对池化窗口覆盖区域内的元素取最大值,得到输出特征图的像素值。当池化窗口在图片上滑动时,会得到整张输出特征图。池化窗口的大小称为池化大小,用表示。在卷积神经网络中用的比较多的是窗口大小为,步长也为2的池化。
与卷积核类似,池化窗口在图片上滑动时,每次移动的步长称为步幅,当宽和高方向的移动大小不一样时,分别用和表示。也可以对需要进行池化的图片进行填充,填充方式与卷积类似,假设在第一行之前填充行,在最后一行后面填充行。在第一列之前填充列,在最后一列之后填充列,则池化层的输出特征图大小为:
在卷积神经网络中,通常使用大小的池化窗口,步幅也使用2,填充为0,则输出特征图的尺寸为:
通过这种方式的池化,输出特征图的高和宽都减半,但通道数不会改变。
03
ReLU激活函数
前面介绍的网络结构中,普遍使用Sigmoid函数做激活函数。在神经网络发展的早期,Sigmoid函数用的比较多,而目前用的较多的激活函数是ReLU。这是因为Sigmoid函数在反向传播过程中,容易造成梯度的衰减。让我们仔细观察Sigmoid函数的形式,就能发现这一问题。
Sigmoid激活函数定义如下:
ReLU激活函数的定义如下:
下面的程序画出了Sigmoid和ReLU函数的曲线图:
# ReLU和Sigmoid激活函数示意图import numpy as npimport matplotlib.pyplot as pltimport matplotlib.patches as patches
plt.figure(figsize=(10, 5))
# 创建数据xx = np.arange(-10, 10, 0.1)
# 计算Sigmoid函数s = 1.0 / (1 + np.exp(0. - x))
# 计算ReLU函数y = np.clip(x, a_min=0., a_max=None)
###################################### 以下部分为画图代码f = plt.subplot(121)plt.plot(x, s, color='r')currentAxis=plt.gca()plt.text(-9.0, 0.9, r'$y=Sigmoid(x)$', fontsize=13)currentAxis.xaxis.set_label_text('x', fontsize=15)currentAxis.yaxis.set_label_text('y', fontsize=15)
f = plt.subplot(122)plt.plot(x, y, color='g')plt.text(-3.0, 9, r'$y=ReLU(x)$', fontsize=13)currentAxis=plt.gca()currentAxis.xaxis.set_label_text('x', fontsize=15)currentAxis.yaxis.set_label_text('y', fontsize=15)
plt.show()
- 梯度消失现象
在神经网络里面,将经过反向传播之后,梯度值衰减到接近于零的现象称作梯度消失现象。
从上面的函数曲线可以看出,当x为较大的正数的时候,Sigmoid函数数值非常接近于1,函数曲线变得很平滑,在这些区域Sigmoid函数的导数接近于零。当x为较小的负数的时候,Sigmoid函数值非常接近于0,函数曲线也很平滑,在这些区域Sigmoid函数的导数也接近于0。只有当x的取值在0附近时,Sigmoid函数的导数才比较大。可以对Sigmoid函数求导数,结果如下所示:
从上面的式子可以看出,Sigmoid函数的导数最大值为。前向传播时,;而在反向传播过程中,x的梯度等于y的梯度乘以Sigmoid函数的导数,如下所示:
使得x的梯度数值最大也不会超过y的梯度的。
由于最开始是将神经网络的参数随机初始化的,x很有可能取值在数值很大或者很小的区域,这些地方都可能造成Sigmoid函数的导数接近于0,导致x的梯度接近于0;即使x取值在接近于0的地方,按上面的分析,经过Sigmoid函数反向传播之后,x的梯度不超过y的梯度的,如果有多层网络使用了Sigmoid激活函数,则比较靠前的那些层梯度将衰减到非常小的值。
ReLU函数则不同,虽然在的地方,ReLU函数的导数为0。但是在的地方,ReLU函数的导数为1,能够将y的梯度完整的传递给x,而不会引起梯度消失。
04
总结
本文重点展开讲解了卷积神经网络里面的常用模块,如池化和Relu。在后期课程中,将继续为大家带来内容更丰富的课程,帮助学员快速掌握深度学习方法。