Tensorflow 多元线性回归实例

@@@@@@@@@@@@@@@@@@@@
基于MOOC中国慕课大学，浙江大学城市学院课程：深度学习应用开发-TensorFlow实践
基于Tensorflow的版本： 2.0.0-beta0 和 Jupyter 编程工具
@@@@@@@@@@@@@@@@@@@@

多元线性回归实例：波士顿房价预测

通过给予的506行、13列数据来对房价进行预测，其中包含了12列样本特征和1列样本标签

准备数据

加载tensorflow库等，并读取数据，显示数据的一些基本信息：

# 2020-3-23 多元线性回归之波士顿房价预测

import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# shuffle函数的作用是：
# scale函数的作用是：对数据做归一化和标准化的处理

from sklearn.utils import shuffle
from sklearn.preprocessing import scale

# 通过pandas库中的read_csv函数来加载数据 注意自己的数据文件的目录
df = pd.read_csv("Mooc/第六周/data/boston.csv",header = 0)

# 显示数据的一些基本信息（条数、平均值、最小值、最大值、上、下分位数等）
print(df.describe())

上图显示了数据的一些基本信息，如CRIM代表了城市的犯罪率，ZN代表了住宅面积超过25000，INDUS代表了城镇非零售商用土地的比例，CHAS代表了边界河流是1，否则是0，NOX代表了一氧化氮浓度，RM代表了住宅平均房间数 等

df.head(3) # 显示数据的头三行
df.tail(3) # 显示数据的尾三行

上图是数据头三行的具体数值的展示情况，由此可知数据的具体值，一行中的数据从0.00632 ~ 296 特征数据之间的差异是比较大的

ds = df.values
print(ds)
print(ds.shape) # 输出数据的维度 （本例中的数据是2维数据，由506行和13列组成）因此是（506，13）

上图是读入数据的具体值，通过这种方式可以看到每个 特征 数据的大致范围 ，例如第一行第一列，数据的大致范围为 0.00632~0.10959

特征值、标签值的划分：这里前12列划分为特征值，最后1列划分为标签值

# x_data 前12列划分为特征值    ds[:,:12] 取了506行,1-12列,因为是2维的数据，所以ds[:,:]这样写
x_data = ds[:,:12]
# y_data 最后1列划分为标签值   ds[:,12]  取了506行，第12列            
y_data = ds[:,12]
print(x_data,x_data.shape)
print(y_data,y_data.shape)

本图展示的是，在数据没有做归一化处理的前提下，进行了训练之后产生损失函数的具体值，图中显示的nan是代表了

因此要对数据进行归一化处理，处理如下（方式一）

# 对训练数据做[0-11列] 做（0-1）归一化
 for i in range(12):
    # 这一行中的（每个值减去这一列中的最小值）除以 （这一列中的最大值减去这一列中的最小值）
    x_data[:,i] = (x_data[:,i]- x_data[:,i].min())/(x_data[:,i].max() - x_data[:,i].min())

数据集的划分：这里前300条划分为训练集，100条划分为验证集，剩余数据划分为测试集

因为本例中的数据只有506条不是很多，所以采用训练集、验证集和测试集的划分，避免对测试集的反复从而降低模型的过拟合几率
这里的数据划分方式采用了留出法进行划分，训练集：验证集：测试集的划分比例约为：6：2：2。

#划分数据集
train_num = 300 #训练集数目
valid_num = 100 #验证集数目
test_num = len(x_data) - train_num - valid_num #测试集数目  506 - 训练集 - 验证集

#训练集划分 列表中的0-300的元素
x_train = x_data[:train_num]  
y_train = y_data[:train_num]  

#验证集划分 列表中的300-400的元素
x_valid = x_data[train_num : train_num + valid_num]
y_valid = y_data[train_num : train_num + valid_num] 

#测试集划分 列表中的400 - 506的元素
x_test = x_data[train_num + valid_num : train_num + valid_num + test_num]
y_test = y_data[train_num + valid_num : train_num + valid_num + test_num]

归一化处理（方式二）

# 调用 scale 函数对数据进行归一化处理，并用cast函数对数据的类型转换，转换成 float32 类型的数据
x_train = tf.cast(scale(x_train),dtype=tf.float32)
x_valid = tf.cast(scale(x_valid),dtype=tf.float32)
x_test = tf.cast(scale(x_test),dtype=tf.float32)

# 创建待优化变量
# random.normal([12,1] 生成数据 mean 是平均数，stddev 是标准差 生成了一个 12 行 1 列 的二维数组
W = tf.Variable(tf.random.normal([12,1],mean = 0.0,stddev = 1.0,dtype = tf.float32))
# zeros 函数生成 了一维的张量，里面的值是 0 
B = tf.Variable(tf.zeros(1),dtype = tf.float32)

上图表示生成的二维数组，其中12行1列

构建模型

模型为y=w*x+b 不过这里的w和b不是一个标量，是一个向量，执行的是矩阵叉乘，所以调用 tf.matmul 函数

#构建模型
# 定义模型函数
def model(x,w,b):
    return tf.matmul(x,w) + b

# 定义均方误差损失函数
def loss(x,y,w,b):
    err = model(x,w,b)- y
    squared_err = tf.square(err)
    return tf.reduce_mean(squared_err)

#定义梯度计算函数
#计算样本数据[x,y]在参数[w,b]点上的梯度

def grad(x,y,w,b):
    with tf.GradientTape() as tape:
        loss_ = loss(x,y,w,b)
    return tape.gradient(loss_,[w,b]) # 返回梯度向量

# 定义模型的各种参数
training_epochs = 50 # 迭代次数
learning_rate = 0.001 # 学习率

batch_size = 10 # 批量训练一次的样本数

optimizer = tf.keras.optimizers.SGD(learning_rate)# 创建优化器，指定学习率

训练模型

共进行 50 轮迭代，每次迭代的步数是 30 步

#训练模型

loss_list_train = [] #用于保存训练集loss值的列表
loss_list_valid = [] #用于保存验证集loss值的列表

# 全部的步数 ，这里是用 训练数据的样本数 除以 批量训练一次的样本数
total_step = int(train_num/batch_size)

for epoch in range(training_epochs):

    for step in range(total_step):
    	
    	# 这是小批量训练
    	# 取每次的训练数据，训练数据是 每次（step） * 这一次中批量训练的样本数 到 下一次（step + 1），后面是一列的全部数据
        xs = x_train[step * batch_size:(step + 1) * batch_size,:]
        # 取每次的标签数据，标签数据是 每次（step） * 这一次中批量训练的样本数 到 下一次（step + 1），后面是一列的全部数据
        ys = y_train[step * batch_size:(step + 1) * batch_size]
        
        # 把 xs,ys,W,B 带入梯度函数中进行计算
        grads = grad(xs ,ys , W, B) # 计算梯度
        
        # 把  这里我没有写完？？？？？？？
        optimizer.apply_gradients(zip(grads,[W,B]))
    
    loss_train = loss(x_train, y_train, W, B).numpy() # 计算当前轮的训练集损失
    # 这里的验证集充当了之前 一元线性回归模型中测试集的作用
    loss_valid = loss(x_valid, y_valid, W, B).numpy() # 计算当前轮的验证集损失
    
    loss_list_train.append(loss_train)
    loss_list_valid.append(loss_valid)
    
    print("epoch = {:3d},train_loss ={:.4f},valid_loss = {:.4f}".format(epoch+1,loss_train,loss_valid) )

# 用可视化来展示损失
plt.xlabel("Epochs")
plt.ylabel("loss")
plt.plot(loss_list_train,'blue',label="Train Loss")
plt.plot(loss_list_valid,'red',label="Valid Loss")

plt.legend(loc = 1)# 通过参数loc指定图例位置，这里是啥作用？？？

# 查看 测试集 的损失
print("Test_loss:{:.4f}".format(loss(x_test, y_test, W, B).numpy()))

进行预测

# 模型预测
test_house_id = np.random.randint(0,test_num)
y = y_test[test_house_id]
y_pred = model(x_test,W,B)[test_house_id]
y_predit = tf.reshape(y_pred,()).numpy()
print("House_id",test_house_id,"Actual value",y,"Predicted value",y_predit)

课后作业

课后作业的代码：

说一下调参过程：对于迭代次数和学习率的调整

1. 下图所展示的图象是迭代次数为500次，学习率为0.001 训练集损失数据 和 验证集损失数据 图象
   
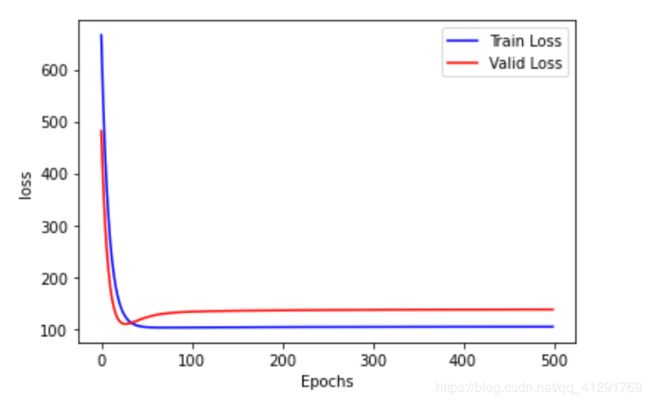
   此时测试集的损失为：Test_loss:144.7368
   此时预测值为：House_id 24 Actual value 11.7 Predicted value 27.926445

由预测值和测试集损失可知：损失较大，且预测值与真实值之间的误差大约为16，很不理想
由图象可知，模型过拟合，50后面的值对于损失降低的影响不大，降低迭代次数，迭代次数降低至50。

2. 下图所展示的图象是迭代次数为50次，学习率为0.001 训练集损失数据 和 验证集损失数
   
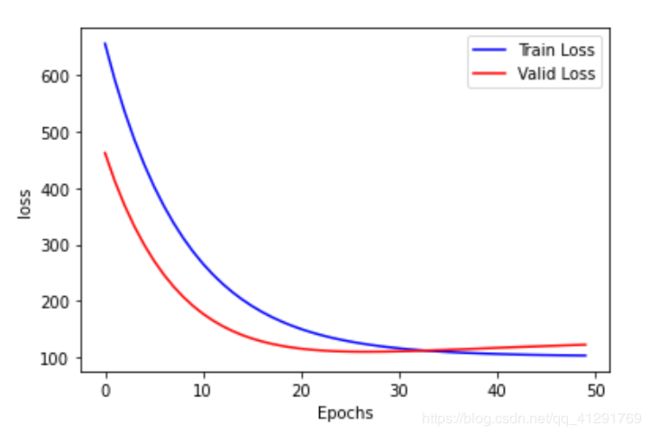
   此时测试集的损失为：Test_loss:115.1757
   此时预测值为：House_id 61 Actual value 17.7 Predicted value 23.338572

由预测值和测试集损失可知：损失较大，且预测值与真实值之间的误差大约为5，效果不理想
图像在30点之后的数据基本趋于稳定，下次迭代次数改为30

3. 下图所展示的图象是迭代次数为30次，学习率为0.001 训练集损失数据 和 验证集损失数
   
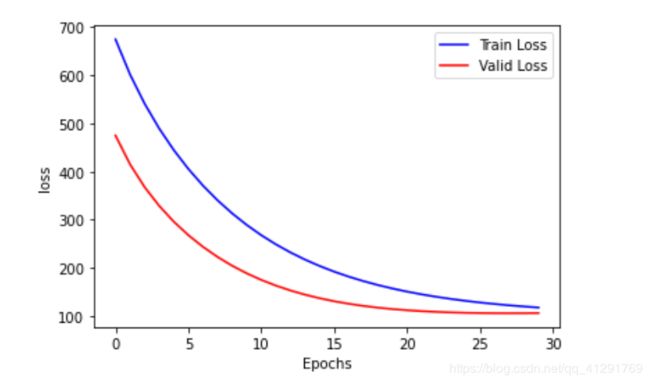
   此时测试集的损失为：Test_loss:69.3510
   此时预测值为：House_id 30 Actual value 14.5 Predicted value 21.877203

由预测值和测试集损失可知：损失较大，且预测值与真实值之间的误差大约为7，效果不好

4. 下图所展示的图象是迭代次数为30次，学习率为0.0001 训练集损失数据 和 验证集损失数
   
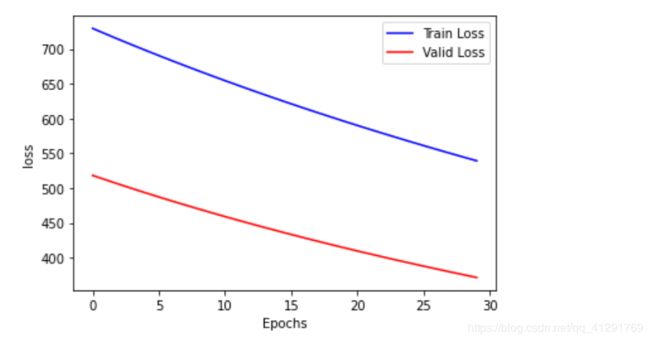
   此时测试集的损失为：Test_loss:170.7032
   此时预测值为：House_id 34 Actual value 11.7 Predicted value 1.479567

此时可以看到，模型还不如上次，因为学习率降低了，导致了模型的欠拟合，每次梯度下降的数值变小了，此时欠拟合，因此学习率数值应该为0.001附近，此时调整为0.00095

5. 下图所展示的图象是迭代次数为30次，学习率为0.00095 训练集损失数据 和 验证集损失数
   
   此时测试集的损失为：Test_loss:65.5066
   此时预测值为：House_id 101 Actual value 22.4 Predicted value 22.305607

此时可以看到，模型在28轮左右时变化基本趋于稳定，模型收敛