两角和与差的正弦、余弦、正切公式的证明
1、关于\(cos(\alpha-\beta)=cos\alpha cos\beta+sin\alpha sin\beta\)的证明思路:
思路一:复数法
思路二:两点间距离公式
思路三:余弦定理
思路四:向量方法
向量方法的证明过程
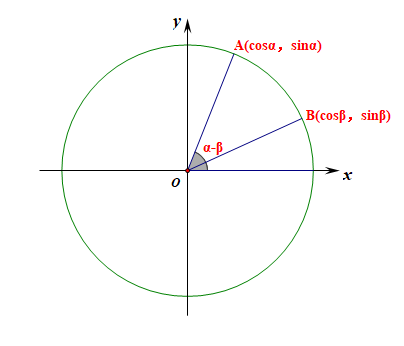
如图所示的单位圆,我们先看两个角都是锐角\((\alpha>\beta)\)的情形;
角\(\alpha\)和\(\beta\)的终边分别交单位圆于点A和B,则根据三角函数的定义可知,\(A(cos\alpha,sin\alpha)\)、\(B(cos\beta,sin\beta)\)
则有\(\overrightarrow{OA}=(cos\alpha,sin\alpha)\),\(\overrightarrow{OB}=(cos\beta,sin\beta)\)
由向量的內积定义可知,\(\overrightarrow{OA}\cdot \overrightarrow{OB}=|\overrightarrow{OA}||\overrightarrow{OB}|cos<\overrightarrow{OA},\overrightarrow{OB}>=cos(\alpha-\beta)\)
又由向量的內积的坐标运算可知,\(\overrightarrow{OA}\cdot \overrightarrow{OB}=cos\alpha cos\beta+sin\alpha sin\beta\)
则有\(cos(\alpha-\beta)=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\)
当两个角是其他情形时,\(\alpha-\beta\)和上面的情形相比,会相差\(2k\pi(k\in Z)\),则由诱导公式可知,仍然满足\(\overrightarrow{OA}\cdot \overrightarrow{OB}=|\overrightarrow{OA}||\overrightarrow{OB}|cos<\overrightarrow{OA},\overrightarrow{OB}>=cos(\alpha-\beta)\)
故仍有\(cos(\alpha-\beta)=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\),证毕。
2、几个公式的关系:
- 用\(cos(\alpha-\beta)=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\)证明\(cos(\alpha+\beta)\)
由于公式中的\(\alpha、\beta\in R\),则可以用\(-\beta\)替换上式中的\(\beta\),得到
\(cos(\alpha-(-\beta))=cos\alpha\cdot cos(-\beta)+sin\alpha\cdot sin(-\beta)\),即
\(cos(\alpha+\beta)=cos\alpha\cdot cos\beta-sin\alpha\cdot sin\beta\),证毕。
- 用\(cos(\alpha-\beta)=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\)证明\(sin(\alpha+\beta)\)
\(sin(\alpha+\beta)=cos[\cfrac{\pi}{2}-(\alpha+\beta)]=cos[(\cfrac{\pi}{2}-\alpha)-\beta]\)
\(=cos(\cfrac{\pi}{2}-\alpha)\cdot cos\beta+sin(\cfrac{\pi}{2}-\alpha)\cdot sin\beta=sin\alpha cos\beta+cos\alpha sin\beta\)
即\(sin(\alpha+\beta)=sin\alpha cos\beta+cos\alpha sin\beta\)
3、举例说明如何使用公式
正用:如\(sin(\alpha+\beta)=sin\alpha cos\beta+cos\alpha sin\beta\),我们用两个单角\(\alpha\)和\(\beta\)的正弦和余弦值的代数式,就可以计算两角和的正弦\(sin(\alpha+\beta)\)
逆用:如\(cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta=cos(\alpha-\beta)\),
变用:比如分式形式的公式,\(tan(\alpha+\beta)=\cfrac{tan\alpha+tan\beta}{1-tan\alpha\cdot tan\beta}\),我们对其做变形,
还可以这样用\(tan(\alpha+\beta)\cdot (1-tan\alpha\cdot tan\beta)=tan\alpha+tan\beta\)
如果将其放置到三角形中,由\(A+B+C=\pi\)可知\(C=\pi-(A+B)\),则有\(tan(A+B)=-tanC\)
代入上式则有\(tan(A+B)\cdot (1-tanA\cdot tanB)=tanA+tanB\),
即\(-tanC\cdot (1-tanA\cdot tanB)=tanA+tanB\),
整理则有\(tanA+tanB+tanC=tanA\cdot tanB \cdot tanC\)。
活用:比如求值\(\cfrac{1-tan15^{\circ}}{1+tan15^{\circ}}=\cfrac{tan45^{\circ}-tan15^{\circ}}{1+tan45^{\circ}\cdot tan15^{\circ}}=tan30^{\circ}=\cfrac{\sqrt{3}}{3}\)
4、常用的公式结论
\(tanA+tanB+tanC=tanA\cdot tanB \cdot tanC\)。
\((1+tan22^{\circ})\cdot (1+tan23^{\circ})=2\)
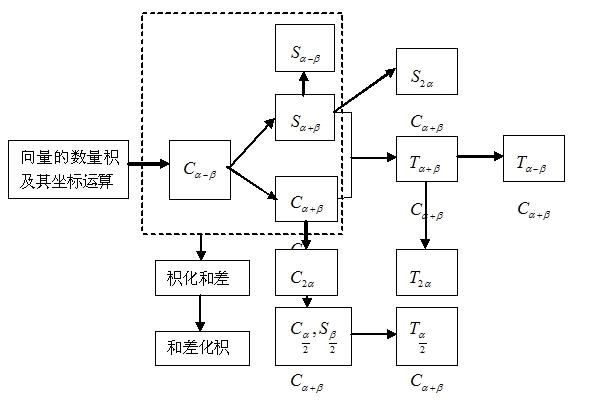
5、证明线索
\(C_{\alpha-\beta}\uparrow C_{\alpha+\beta}\uparrow\)
\(C_{\alpha+\beta}\uparrow\)