7-1 树结构 和 二叉树
7-1 树结构 和 二叉树
前面讲的都是 线性存储结构,而树是一种典型的非线性存储结构,一个元素可以有多个直接后继元素。
1.一些术语
①叶子:没有后继节点的 结点称为叶子节点;
②分支节点: 非叶子节点;
③节点的度: 直接后继节点的数目;
④子节点: 某一个节点的直接后继节点;
⑤父节点:某个子节点的直接前驱节点;
⑦兄弟:具有同一父节点的 一群节点;
⑧节点的层次: 根节点为1,其它节点的层次等于它的父节点+1;
⑨树的深度:节点的最大层次值;
⑩有序树 和 无序树: 如果某棵树的节点都是按从左到右的顺序排列,交换两个节点的位置会产生一个不同的树,那么此树就为有序树;反之为 无序树;
⑪森林: 不同的树的集合;如果一棵树删除了根节点,那么剩下的子树就组成一片森林。
2.关于树的根节点的数目
这个似乎一直以来都有点矛盾,不同的书上可能说的不一样。
有的书说,树有且只有一个根节点,即根节点数目为1;
有的书说,树的根节点可以为0,这时候称为空树。
而且连网上的各种资料也都存在这两种说法,你可以在百度百科上查树结构和空树的定义,发现这两种说法都存在。
那就看具体情况来回答这个问题。
3.二叉树
简单地理解,满足以下两个条件的树就是二叉树:
①本身是有序树;!!!
②树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
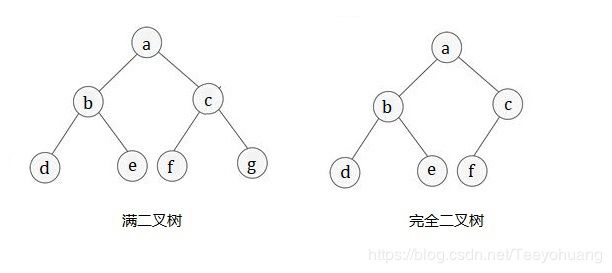
A 满二叉树
定义:
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
性质:
①满二叉树中第 i 层的节点数为 2^ (i-1) 个。(根节点层数是1)
②深度为 i 的满二叉树必有 2^i - 1 个节点(等比数列公式) ,叶子数为 2^ (i-1)。
③满二叉树中不存在度为 1 的节点,每一个分支点都有两棵深度相同的子树,且叶子节点都在最底层。
④具有 n 个节点的满二叉树的深度为 log2 (n+1)。
B 完全二叉树
定义:
如果二叉树中 除去最后一层节点 为满二叉树,且最后一层的结点依次从左到右有序分布,则此二叉树被称为完全二叉树。
或者说,一个具有n个节点的二叉树,如果其节点编号 和 一颗满二叉树的1---n个节点的编号完全一致,那这棵树就是完全二叉树。
可以看到,满二叉树一定是 完全二叉树, 完全二叉树 不一定是 满二叉树,
性质:(由于满二叉树 一定是 完全二叉树,所以以下性质对满二叉树依然适用)
①N 个结点的完全二叉树的深度为 ⌊log2 N⌋+1。(向下取整再加1)
②如果将含有的结点按照层次从左到右依次标号,对于任意一个结点 i 完全二叉树还有以下几个结论成立:
当 i>1 时,父亲结点为结点 [i/2] (向下取整)。(i=1 时,表示的是根结点,无父亲结点)
i 节点的左孩子( 如果有的话 )是节点 2*i 。
i 节点的右孩子( 如果有的话 )是节点 2*i +1。
4.二叉树的存储结构
A 顺序存储结构,
使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。
换句话说,只有完全二叉树才可以使用顺序表存储!
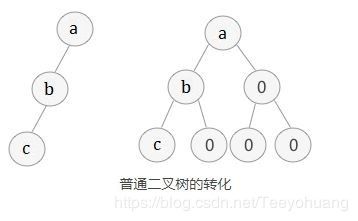
因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。方法很简单,人为添加一些并不存在的空节点(其元素值为“空”),使之成为一颗完全二叉树的形式。但是这种方式明显会浪费大量内存,此时应考虑链式存储方式。
完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。
从顺序表中还原完全二叉树也很简单。我们知道,完全二叉树具有这样的性质,将树中节点按照层次并从左到右依次标号(1,2,3,...),若节点 i 有左右孩子,则其左孩子节点为 2*i,右孩子节点为 2*i+1。此性质可用于还原数组中存储的完全二叉树。
B 链式存储结构
只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。不必非得是完全二叉树
其节点结构由 3 部分构成:
指向左孩子节点的指针(Lchild);节点存储的数据(data);指向右孩子节点的指针(Rchild)
这样的链表结构,通常称为二叉链表。
typedef struct BiTNode{
TElemType data; //数据域
struct BiTNode *lchild, *rchild;//左右孩子指针
}BiTNode;
其实,二叉树的链式存储结构远不止图 2 所示的这一种。例如,在某些实际场景中,可能会做 "查找某节点的父节点" 的操作,这时可以在节点结构中再添加一个指针域,用于各个节点指向其父亲节点,
这样的链表结构,通常称为三叉链表。
typedef struct BiTNode{
TElemType data; //数据域
struct BiTNode *lchild, *rchild;//左右孩子指针
struct BiTNode *parent; //父节点指针
}BiTNode;
5.二叉树的四种遍历方法
二叉树可以记根节点为D,左子树为L,右子树为R
typedef struct BiTNode{
int data;//数据域
struct BiTNode *L;//左孩子指针
struct BiTNode *R;//右孩子指针
}Bnode;
①先序遍历
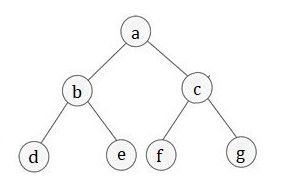
先序的先,是指的根节点的先。 D L R的顺序,且下层的子树也是按这个D L R 的顺序
此二叉树 先序遍历就是 a-b-d-e-c-f-g
//先序遍历
void PreOrder(Bnode *BT){
if ( BT != nullptr ) {
cout<
PreOrder(BT->L);//访问该结点的左孩子
PreOrder(BT->R);//访问该结点的右孩子
}
return;
}
②中序遍历
中序的中,是根节点居中, L D R ,且下层的子树也是按这个L D R的顺序
此二叉树 中序遍历就是 d-b-e-a-f-c-g
//中序遍历
void InOrder(Bnode *BT){
if (BT != nullptr ) {
InOrder(BT->L);//访问该结点的左孩子
cout<
InOrder(BT->R);//访问该结点的右孩子
}
return;
}
③后序遍历
后序的后,是根节点居后, L R D ,且下层的子树也是按这个L R D 的顺序
后序遍历顺序 d-e-b-f-g-c-a
//后序遍历
void PostOrder(Bnode *BT){
if (BT != nullptr) {
PostOrder(BT->L);//访问该结点的左孩子
PostOrder(BT->R);//访问该结点的右孩子
cout<
}
return;
}
上面三种方法其实都是利用的递归的思想,符合二叉树递归的定义。
其实也可以用栈来实现
④二叉树层次遍历
按照二叉树中的层次从左到右依次遍历每层中的结点。具体的实现思路是:
通过使用队列的数据结构,从树的根结点开始,依次将其左孩子和右孩子入队。
而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。
首先,根结点 a 入队;
根结点 a 出队,出队的同时,将左孩子 b 和右孩子 c 分别入队;
队头结点 b 出队,出队的同时,将结点 b 的左孩子 d 和右孩子 e 依次入队;
队头结点 c 出队,出队的同时,将结点 3 的左孩子 f 和右孩子 g 依次入队;
不断地循环,直至队列内为空。