How to do Zero-Knowledge from Discrete-Logs in under 7kB
We recently had our annual conference for the Academic Centres of Excellence in the UK and I am proud that Jonathan Bootle from UCL won the PhD student elevator pitch competition. I’ll now hand over the rest of the blog post to Jonathan to explain the communication reduction technique for zero-knowledge arguments he presented.
— Jens Groth
In zero-knowledge arguments, a verifier wants to check that a prover possesses secret knowledge satisfying some stated conditions. The prover wants to convince the verifier without disclosing her secrets. Security is based on cryptographic assumptions, like the discrete logarithm assumption. In 1997, Cramer and Damgård produced a discrete log argument requiring the prover to send N pieces of data to the verifier, for a statement of size N. Groth improved this to √N in 2009 and for five years, this was thought to be the best possible. That is, until cryptographers at UCL, including myself, discovered an incredible trick, which shattered the previous record. So how does it work?
The first step is to compile the statement into the correct format for our protocol. Existing compilers take practical statements, such as verifying the correct execution of a C program, and convert them into a type of circuit. We then convert this circuit into a vector equation for the verifier to check. A circuit of size N produces a vector of size roughly N. So far, so good.
We also need use a commitment scheme, which works like a magician’s envelope. By committing to a hidden value, it can be fixed, and revealed later.
In previous works in the discrete logarithm setting, the prover commits to the vector using a single commitment.
Later the prover reveals the whole vector. This gives high communication costs, and was a major bottleneck.
We discovered a rare and extraordinary property of the commitment scheme which allowed us to cut a vector in half and compress the two halves together. Applying the same trick repeatedly produces a single value which is easy to send, and drastically reduces the communication costs of the protocol.
We begin with a vector of roughly N elements. If we repeatedly cut the vector in half, it takes log(N) cuts to produce a vector containing only a single element. Each time that the prover cuts a vector in half, they must make new commitments to enable the verifier to check the shorter vectors produced. Overall, roughly log(N) new commitments are produced, so the prover must send about log(N) values to the verifier. This is a dramatic improvement from √N. To put this in perspective, doubling the size of the statement only adds a constant amount of data for the prover to send.
Of course, it is possible to base security on other cryptographic assumptions, but other efficient protocols often use very strong and untested assumptions which have yet to receive a high level of scrutiny. By contrast, the discrete logarithm assumption has been used and studied for over three decades.
Is this just a theoretical advance? Far from it. Our protocol has a working Python implementation, which has been extensively benchmarked. By combining our code with the compilers that I mentioned earlier, we verified the correct execution of C programs. By sending under 7kB of data each time, we can verify matrix multiplications, simulations of the motion of gas molecules, and SHA-1 hashes. It’s nice to see theory that compiles and works.
How do Bulletproofs Work?
The basis of confidential transactions is to replace the input and output amounts with Pedersen Commitmentsdef. It is then publicly verifiable that the transactions balance (the sum of the committed inputs is greater than the sum of the committed outputs, and all outputs are positive), while keeping the specific committed amounts hidden. This makes it a zero-knowledge transaction. The transaction amounts must be encoded as integersmodqintegersmodq, which can overflow, but are prevented from doing so by making use of range proofs. This is where Bulletproofs come in. The essence of Bulletproofs is its ability to calculate proofs, including range proofs, from inner-products.
The prover must convince the verifier that commitment C(x,r)=xH+rG contains a number such that x∈[0,2n−1]. If a=(a1,...,an)∈0,1n is the vector containing the bits of x, the basic idea is to hide all the bits of the amount in a single vector Pedersen Commitment. It must then be proven that each bit satisfies ω(ω−1)=0, i.e. each ωω is either 0 or 1, and that they sum to x. As part of the ensuing protocol, the verifier sends random linear combinations of constraints and challenges ∈Zp to the prover. The prover is then able to construct a vectorized inner product relation containing the elements of aa, the constraints and challenges ∈Zp, and appropriate blinding vectors ∈Znp.
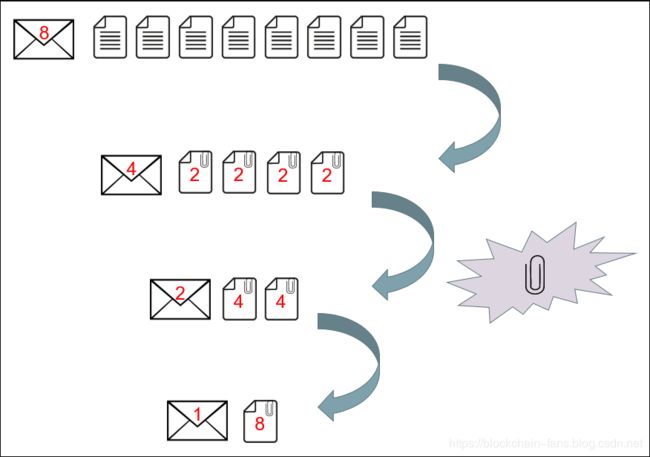
These inner product vectors have size nn that would require many expensive exponentiations. The Pedersen Commitment scheme, shown in Figure 1, allows for a vector to be cut in half, and for the two halves to be compressed together, each time calculating a new set of Pedersen Commitment generators. Applying the same trick repeatedly, log2n times, produces a single value. This is applied to the inner product vectors; they are reduced interactively with a logarithmic number of rounds by the prover and verifier into a single multi-exponentiation of size 2n+2log2(n)+1. This single multi-exponentiation can then be calculated much faster than nn separate ones. All of this is made non-interactive using the Fiat-Shamir Heuristicdef.
Figure 1: Vector Pedersen Commitment Cut and Half ([12], [63])
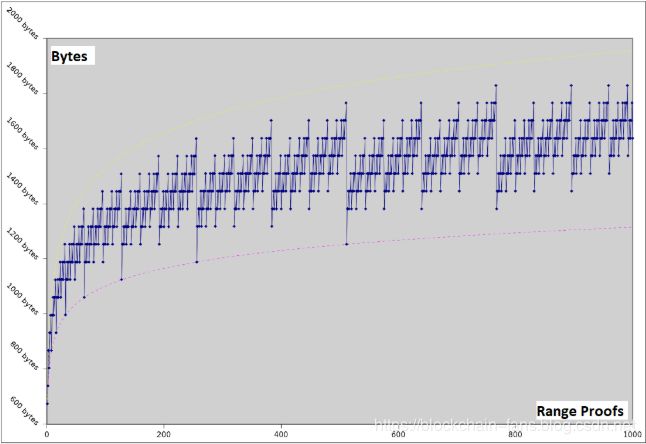
Bulletproofs only rely on the discrete logarithm assumption. In practice, this means that Bulletproofs are compatible with any secure elliptic curve, making them extremely versatile. The proof sizes are short; only [2log2(n)+9] elements are required for the range proofs and [log2(n)+13]elements for arithmetic circuit proofs, with nn denoting the multiplicative complexity. Additionally, the logarithmic proof size enables the prover to aggregate multiple range proofs into a single short proof, as well as to aggregate multiple range proofs from different parties into one proof (refer to Figure 2) ([1], [3], [5]).
Figure 2: Logarithmic Aggregate Bulletproofs Proof Sizes [3]
If all Bitcoin transactions were confidential, approximately 50 million UTXOs from approximately 22 million transactions would result in roughly 160GB range proof data, when using current/linear proof systems and assuming use of 52 bits to represent any value from 1 satoshi up to 21 million bitcoins. Aggregated Bulletproofs would reduce the data storage requirement to less than 17GB [[1]].
In Mimblewimble, the blockchain grows with the size of the UTXO set. Using Bulletproofs as a drop-in replacement for range proofs in confidential transactions, the size of the blockchain would only grow with the number of transactions that have unspent outputs. This is much smaller than the size of the UTXO set [1].
The recent implementation of Bulletproofs in Monero on 18 October 2018 saw the average data size on the blockchain per payment reduce by ~73% and the average USD-based fees reduce by ~94.5% for the period 30 August 2018 to 28 November 2018 (refer to Figure 3).
Figure 3: Monero Payment, Block and Data Size Statistics
The full paper is by Jonathan Bootle, Andrea Cerulli, Pyrros Chaidos, Jens Groth and Christophe Petit and was published at EUROCRYPT 2016.
ref:
https://www.benthamsgaze.org/2016/10/25/how-to-do-zero-knowledge-from-discrete-logs-in-under-7kb/
https://tlu.tarilabs.com/cryptography/bulletproofs-and-mimblewimble/MainReport.html