单源点最短路径问题(Dijkstra算法)
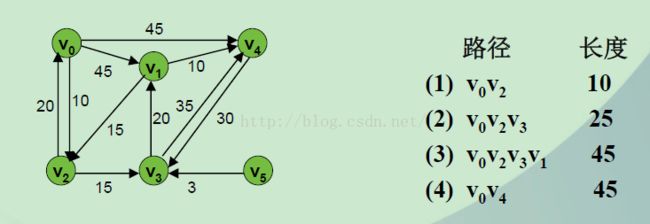
如图所示。设v0是起始点,求v0到其它各结点的最短路径。
设visited是已经生成了最短路径的结点集合(包括v0),对于当前不在visited中的结点w,记DIST(w)是从v0开始,只经过visited中的结点而在w结束的那条最短路径的长度;
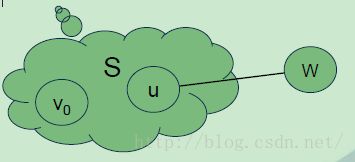
(1) 如果下一条最短路径是到结点u,则这条路径是从结点v0出发在u处终止,且只经过那些在visited中的结点,即由v0至u的这条最短路径上的所有中间结点都是visited中的结点:设w是这条路径上的任意中间结点,则从v0到u的路径也包含了一条从v0到w的路径,且其长度小于从v0到u的路径长度,如下图:
(2) 所生成的下一条路径的终点u必定是所有不在visited内的结点中且具有最小距离DIST(u)的结点。
(3) 如果选出了这样结点u并生成了从v0到u的最短路径之后,结点u将成为visited中的一个成员。此时,那些从v0出发,只经过visited中的结点并且在visited外的结点w处结束的最短路径可能会减少——DIST(w)的值变小:如果这样的路径的长度发生了改变,则这些路径必定是一条从v0开始,经过u然后到w的更短的路所致,概念如下图:
因此整个算法的流程为:
假设存在Graph=
1.从(V-visited)中,即未加入的u的集合中选择使dist[vi]值最小的顶点vi,将vi加入到visited中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[u]+Graph[u][j]})
3.直到说visited=V,停止。
#include
#include
#include
#include
using namespace std;
#define max INT_MAX;
int **Graph;//n个顶点的有向图,包含e条边
int n;
int e;
//读入数据
void input();
//g为有向图
//dist为v0到各点最短路径长度
//path为记录的从v0到某点的最短路径
void Dijkstra(int **g, int nsize, int *dist, int *path, int v0);
//从v0到vi的路径
void showPath(int* path, int* dist, int v0, int vi);
int main()
{
input();
/*for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
cout << Graph[i][j] << " ";
cout << endl;
}*/
int *dist = new int[n]; //距离数组
int *path = new int[n]; //路径数组
int v0;
cin >> v0;
Dijkstra(Graph, n, dist, path, v0-1); //从1开始计数就减1,否则去掉
cout << "start " << "end " << "length " << "nodes list " << endl;
for (int i = 0; i < n; i++)
{
if (i != v0)
{
showPath(path, dist, v0-1, i);
}
}
delete dist;
delete path;
delete Graph;
return 0;
}
void input()
{
fstream cin("a.txt");
int start, end, weight;//代表一条s->t权重为weight的边
cin >> n >> e;
Graph = new int*[n];
//初始化有向图
for (int i = 0; i < n; i++)
{
Graph[i] = new int[n];
for (int j = 0; j < n; j++)
{
if (j == i)
Graph[i][j] = 0;//对角线置0
else
Graph[i][j] = 0;
}
}
//读入数据
for (int i = 0; i < e; i++)
{
cin >> start >> end >> weight;
Graph[start - 1][end - 1] = weight; //减1:图中节点从1开始
}
}
void Dijkstra(int **g, int nsize, int *dist, int *path, int v0)
{
bool *visited = new bool[nsize]; //记录已经访问过的点(依次加入的到v0距离最近)
for (int i = 0; i < nsize; i++)//初始化
{
if (i != v0 && g[v0][i] > 0)
{
dist[i] = g[v0][i]; //用初值更新dist
path[i] = v0; //path中存储连接到从v0到i的上一个节点(i前面一个)
}
else //不与v0相邻的,设置权重为无穷大
{
dist[i] = max;
path[i] = -1; //没有连接
}
visited[i] = false; //将所有节点置为未访问过
dist[v0] = 0;
path[v0] = v0;
}
visited[v0] = true; //将v0加入到集合中
for (int i = 1; i < nsize; i++) //将剩余节点(从1到n-1)依次加入到集合visited中
{
int minCost = max;
int u; //即将加入集合visited的点
for (int k = 0; k < nsize; k++) //找到集合外距离v0最近的点
{
if (visited[k] == false && dist[k] < minCost)
{
minCost = dist[k];
u = k;
}
}
visited[u] = true;
for (int j = 0; j < nsize; j++) //每加入一个点就更新dist
{
//比较从dist[v0-->j]与dist[v0-->若干点-->u-->j]
if (visited[j] == false && Graph[u][j] > 0 && dist[j] > minCost + Graph[u][j])
{
dist[j] = minCost + Graph[u][j];
path[j] = u; //j进过w到v0,比j直接到v0原路径近
}
}
}
}
void showPath(int* path, int* dist,int v0, int vi)
{
stack s;
cout << 'v' << v0 << ' '; //start
cout << 'v' << vi << ' '; //end
while (vi != v0)
{
s.push(vi);
vi = path[vi]; //vi位置存储的是v0到vi的上个节点的位置
}
s.push(vi);
cout << dist[vi] << ' '; //distance
while (!s.empty())
{
cout << 'v' << s.top() << ' ';
s.pop();
}
cout << endl;
} 测试数据为:
7 12
1 2 20
1 3 50
1 4 30
2 3 25
2 6 70
3 5 25
3 6 50
4 3 40
4 5 55
5 6 10
5 7 70
6 7 50