图的有权最短路径及Dijkstra算法

图的有权最短路径

• 和有向无权图不同的是，有向有权图相邻两个顶点间的边上被赋予一个连接权值。
• 有权最短路径就是寻找一条路径使得该路径上的权值相加与其他路径相比最小。
• 例如：
  
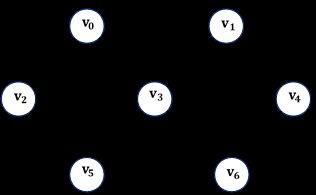
• 上图，顶点 v0 v 0 和 v5 v 5 之间存在多条路径，如 v0→v3→v5 v 0 → v 3 → v 5 、 v0→v3→v6→v5 v 0 → v 3 → v 6 → v 5 等，而最短的路径为 v0→v3→v6→v5 v 0 → v 3 → v 6 → v 5 长度为1+4+1=6。

---

图的有权最短路径算法

• 首先最直观方法是穷举法，穷举出所有可能的路径，再选出最小值。当然复杂度太高不可取。
• 同无权最短路径一样，求有权最短路径同样借助一个与起始顶点（以 v2 v 2 为例）有关的状态信息表。
• 表中同样有三列信息来表述从 v2 v 2 出发，每个顶点的状态改变：
• 包括Known（标识顶点是否被声明已知）、dist（从 v2 v 2 出发使用已知顶点作为中间顶点到目标顶点的距离）、Path（路径中每个顶点上次经过的顶点）。
• 初始化如下：
  
• 我们要求从 v2 v 2 出发当所有顶点的有权最短路径就是要想办法更新与之相关的状态信息表。

---

Dijkstra算法

• Dijkstra算法是贪心算法(greedy algorithm)的典型应用实例，能够有效地解决有权最短路径问题。
• 和无权最短路径一样，Dijkstra算法也是按步分阶段进行：
• 只不过每次采取贪心的策略在未知顶点中选取与起始顶点（ v2 v 2 ）距离最小的点（Known未知；dist最小）来着手操作。
• 首先将其（ v2 v 2 ）Known状态改为已知，接着遍历其（ v2 v 2 ）邻接点，当邻接点（例如 v0、v5 v 0 、 v 5 ）的dist大于其（ v2 v 2 ）dist加上它们的连接权值时，更新邻接点的dist为其（ v2 v 2 ）dist加上它们的连接权值。
• 如此，直到将图中所有 v2 v 2 可达的点遍历完，与之有关的状态信息表也更新完毕，最后从状态信息表中可以得出相关信息。
• 算法复杂度分析：每次寻找最小的dist值花费 O(|V|) O ( | V | ) ，需要寻找 O(|V|) O ( | V | ) 次，故整个算法过程将花费 O(|V|2) O ( | V | 2 ) 来查找最小dist值。
• 每次更新dist为常数时间，共计更新 O(|E|) O ( | E | ) 次，所以总得算法时间复杂度为 O(|E|+O|V|2)=O(|V|2) O ( | E | + O | V | 2 ) = O ( | V | 2 ) 。
• 如果借助优先队列（堆）来查找最小值，时间复杂度可以降低为 O(|E|log|V|) O ( | E | log ⁡ | V | ) 。

Dijkstra算法实现

template<class T>
void Graph::Dijkstra(int index)      // Dijkstra算法实现，目的是为了改变index顶点的状态信息表
{
    Vertex W;
    int MinIndex;
    while (1)
    {
        MinIndex = UnknownMinDistVertex(index);     // 寻找当前index顶点的状态信息表的最小dist值的顶点下标
        if (MinIndex == -1)     // 当MinIndex为-1，表示所有点都被标明已知，结束循环
            break;  
        VSet[index].table[MinIndex].Known = true;       // 标记最小dist值的顶点为已知
        // 遍历当前最小dist值的顶点的邻接表
        for (vector>::iterator iter = VSet[MinIndex].adj_list.begin(); iter != VSet[MinIndex].adj_list.end();iter++)
        {
            if (!VSet[index].table[iter->value].Known)  // 如果其邻接点未被声明已知，则
                if (VSet[index].table[MinIndex].dist + iter->weight < VSet[index].table[iter->value].dist)  
                {   // 如果最小dist顶点dist加上该顶点与其邻接点的连接权值小于其邻接点原有的dist值，则更新其邻接点的dist值
                    VSet[index].table[iter->value].dist = VSet[index].table[MinIndex].dist + iter->weight;
                    VSet[index].table[iter->value].Path = VSet[MinIndex].value;     // 更新最小dist顶点的邻接点的Path值为最小dist顶点（的值，为了方便）
                }
        }
    }
}

---

附图的有权最短路径Dijkstra算法实现C++

#include
#include
#include
#include
#include
using namespace std;

const int INF = 999999;     // 表示无穷大（此例中）

template<class T> class Vertex;             // 提前声明顶点类

template<class T>
class InfoTable {       // 创建一个信息表类
public:
    bool Known;         // 是否被遍历
    int dist;           // 顶点间的距离
    T Path;     // 用顶点关键字表示的路径栏
};

template<class T>
class Vertex {      // 创建一个顶点类
public:
    T value;        // 顶点的关键字值
    vector> adj_list;     // 顶点的邻接表
    InfoTable* table;        // 最短路径时每个顶点的信息栏
    int weight;     // 顶点之间的权重（相邻顶点的连接权值），存放在邻接顶点中，每个顶点与自身的权值为0
    Vertex(T value = 0) :value(value), weight(0) {} // 默认构造函数
};

template<class T>
class Graph {       // 创建一个图类
public:
    vector> VSet;     // 表示顶点的集合
    Graph(int sz) :size(sz) {}  // 构造函数
    Graph(const Graph &G) { size = G.size;VSet = G.VSet; }   // 复制构造函数

    void InitInfoTable();       // 初始化图中顶点的状态信息表

    int UnknownMinDistVertex(int index);    // 找index状态信息表中未知的（Known=0）最小dist顶点（的下标）
    void Dijkstra(int index);       // Dijkstra算法求某个顶点(图中下标为index的顶点)的有权最短路径
    void PrintPath(int index);  // 打印某个节点的最短路径

private:
    int size;                   // 图中顶点的个数
};

template<class T>
void Graph::InitInfoTable()      // 初始化图中顶点的状态信息表
{
    for (int i = 0;i < size;i++)
    {
        VSet[i].table = new InfoTable[size]; // 为每个顶点的状态表申请空间
        for (int j = 0;j < size;j++)
        {
            VSet[i].table[j].Known = false;     // 每个节点都没被经过
            VSet[i].table[j].dist = INF;        // 初始时每个顶点距离为无穷，表示不可达
            VSet[i].table[j].Path = -1;
        }
        VSet[i].table[i].dist = 0;              // 初始时每个顶点距离自身为0
    }
}

template<class T>
int Graph::UnknownMinDistVertex(int index)
{
    int MinIndex = -1;  // 初始化未知最小dist顶点下标为-1
    for (int i = 0;i < size;i++)        
    {
        if (!VSet[index].table[i].Known)        // 首先找到第一个未知的顶点
            MinIndex = i;                       // 如果未知点（未被声明已知的顶点）存在，则更新MinIndex的值
    }

    for (int i = 0;i < size;i++)                // 再一次遍历index顶点的状态信息表
    {
        // 当某个顶点的dist小于当前最小dist值且未知
        if (VSet[index].table[i].dist < VSet[index].table[MinIndex].dist && !VSet[index].table[i].Known)        
            MinIndex = i;               // 更新最小dist值下标
    }
    return MinIndex;
}

template<class T>
void Graph::Dijkstra(int index)      // Dijkstra算法实现，目的是为了改变index顶点的状态信息表
{
    Vertex W;
    int MinIndex;
    while (1)
    {
        MinIndex = UnknownMinDistVertex(index);     // 寻找当前index顶点的状态信息表的最小dist值的顶点下标
        if (MinIndex == -1)     // 当MinIndex为-1，表示所有点都被标明已知，结束循环
            break;  
        VSet[index].table[MinIndex].Known = true;       // 标记最小dist值的顶点为已知
        // 遍历当前最小dist值的顶点的邻接表
        for (vector>::iterator iter = VSet[MinIndex].adj_list.begin(); iter != VSet[MinIndex].adj_list.end();iter++)
        {
            if (!VSet[index].table[iter->value].Known)  // 如果其邻接点未被声明已知，则
                if (VSet[index].table[MinIndex].dist + iter->weight < VSet[index].table[iter->value].dist)  
                {   // 如果最小dist顶点dist加上该顶点与其邻接点的连接权值小于其邻接点原有的dist值，则更新其邻接点的dist值
                    VSet[index].table[iter->value].dist = VSet[index].table[MinIndex].dist + iter->weight;
                    VSet[index].table[iter->value].Path = VSet[MinIndex].value;     // 更新最小dist顶点的邻接点的Path值为最小dist顶点（的值，为了方便）
                }
        }
    }
}

template<class T>
void Graph::PrintPath(int index)
{
    cout << "The InfoTable of V" << index << " is:\n";
    cout << "Vertex Known   dist    Path" << endl;
    for (int i = 0;i < size;i++)    // 打印下标为index的顶点的状态表
    {
        cout << "V" << i << "\t" << VSet[index].table[i].Known << "\t" << VSet[index].table[i].dist
            << "\t" << "V" << VSet[index].table[i].Path << endl;
    }
    cout << "\nShow the weighted shortest paths from V" << index << " to other vertices by Dijkstra Alogrithm: \n";
    stack S;         // 借助栈输出从index顶点出发到各个顶点的无权最短路径
    for (int i = 0;i < size;i++)
    {
        if (i == index)
            continue;
        if (VSet[index].table[i].dist == INF)
        {
            cout << "Unreachable!\n";
            continue;
        }
        cout << "The shortest path from V" << index << " to V" << i << " is "
            << VSet[index].table[i].dist<<" long, and the path is: ";
        int j = i;      // 每次取一个顶点作为开始
        S.push(VSet[j].value);  // 顶点入栈
        while (VSet[index].table[j].Path != -1) // 当遍历指定顶点的“Path”形成路径
        {
            S.push(VSet[index].table[j].Path);  // 将路径上的顶点的Path值入栈
            j = VSet[index].table[j].Path;      // 更新顶点下标
        }
        while (!S.empty())                      // 栈不为空时，打印路径并出栈
        {
            if(S.top() != index)
                cout << "->";
            cout << "V" << S.top();
            S.pop();
        }
        cout << endl;
    }
    cout << endl;
}

int main()
{
    Graph<int> G(7);            // 创建一个图对象G
    Vertex<int> V[] = { Vertex<int>(0), Vertex<int>(1), Vertex<int>(2), Vertex<int>(3),
        Vertex<int>(4), Vertex<int>(5), Vertex<int>(6) };

    V[0].adj_list.push_back(V[1]);  // 顶点V0的邻接表
    V[0].adj_list.push_back(V[3]);  
    V[0].adj_list[0].weight = 2;    // V0与V1的连接权值
    V[0].adj_list[1].weight = 1;    // V0与V3的连接权值

    V[1].adj_list.push_back(V[3]);  // 顶点V1的邻接表
    V[1].adj_list.push_back(V[4]);
    V[1].adj_list[0].weight = 3;    // V1与V2的连接权值
    V[1].adj_list[1].weight = 10;   // V1与V4的连接权值

    V[2].adj_list.push_back(V[0]);  // 顶点V2的邻接表
    V[2].adj_list.push_back(V[5]);  
    V[2].adj_list[0].weight = 4;    // V2与V0的连接权值
    V[2].adj_list[1].weight = 5;    // V2与V5的连接权值

    V[3].adj_list.push_back(V[2]);  // 顶点V3的邻接表
    V[3].adj_list.push_back(V[4]);
    V[3].adj_list.push_back(V[5]);
    V[3].adj_list.push_back(V[6]);
    V[3].adj_list[0].weight = 2;    // V3与V2的连接权值
    V[3].adj_list[1].weight = 2;    // V3与V4的连接权值
    V[3].adj_list[2].weight = 8;    // V3与V5的连接权值
    V[3].adj_list[3].weight = 4;    // V3与V6的连接权值

    V[4].adj_list.push_back(V[6]);  // 顶点V4的邻接表
    V[4].adj_list[0].weight = 6;    // V4与V6的连接权值

    V[6].adj_list.push_back(V[5]);  // 顶点V6的邻接表
    V[6].adj_list[0].weight = 1;    // V6与V5的连接权值

    for (int i = 0;i < 7;i++)
    {
        G.VSet.push_back(V[i]);
    }
    G.InitInfoTable();      // 初始化图中顶点的状态信息表
    G.Dijkstra(0);          // Dijkstra算法求G中顶点V2到其他顶点的有权最短路径
    G.PrintPath(0);         // 打印从V2到其他顶点路径

    system("pause");
    return 0;
}

• 运行结果

The InfoTable of V0 is:
Vertex  Known   dist    Path
V0      1       0       V-1
V1      1       2       V0
V2      1       3       V3
V3      1       1       V0
V4      1       3       V3
V5      1       6       V6
V6      1       5       V3

Show the weighted shortest paths from V0 to other vertices by Dijkstra Alogrithm:
The shortest path from V0 to V1 is 2 long, and the path is: V0->V1
The shortest path from V0 to V2 is 3 long, and the path is: V0->V3->V2
The shortest path from V0 to V3 is 1 long, and the path is: V0->V3
The shortest path from V0 to V4 is 3 long, and the path is: V0->V3->V4
The shortest path from V0 to V5 is 6 long, and the path is: V0->V3->V6->V5
The shortest path from V0 to V6 is 5 long, and the path is: V0->V3->V6

请按任意键继续. . .

---

参考资料

Mark Allen Weiss: 数据结构与算法分析