从霍格沃茨而来的密码学——解读区块链咒语Mimblewimble
导言/林佳谊
关心加密货币圈的人都知道,2018 年底和 2019 年初有两个新币种 Grin 和 Beam 先后上线,即便不打算 ICO,仍从少数核心开发者开始,一路神奇迅速走红矿工圈、投资圈,乃至于成为整个加密货币社区的热议话题。
火红原因在于,Grin 和 Beam 在技术上运用了一个有着魔咒般名称的 Mimblewimble 区块链协议,解决了比特币交易缺乏隐私性的这一大弱点,也就是其每笔交易都有固定地址,只要通过分析比对,用户的身份与交易行为就可能被曝光。Mimblewimble 之名源自于《哈利•波特》小说里的咒语“混淆咒”,它的发明者更用了法语版伏地魔的名字 Tom Elvis Jedusor。
究竟 Mimblewimble 有什么魔力?它除了催生了两个新币种外,还为整个加密货币技术的发展带来了哪些更整体的突破?本周 DeepHash 专栏很高兴又邀请到一位新作者,精通密码学的国内知名公链初创公司 Conflux 研究总监杨光博士,来为本专栏读者讲解 Mimblewimble 的技术原理。而他归纳,MimbleWimble 最主要的三大贡献在于改善比特币的隐私性、可替代性和扩容性。
(来源:Unsplash)
文/杨光(Conflux 研究总监)
今年 315 不知道大家有没有看到一則新闻,当你的手机尝试连接 wifi 时,会把你的 MAC 地址广播出去。其他人可以用 wifi 探针来找到你的 MAC 地址。且因为这是跟手机绑定的,所以就能进一步对应到你的手机号和个人身份等信息。因此大家说,出门最好把 WLAN 给关掉,不要泄露自己的 MAC 地址。但如果是在比特币上,可能连探针都不需要,直接搜地址,就可以找到对应账户的交易记录了。账户上金额的流进流出所有人都能看到。
为什么?因为比特币虽被称为是加密货币,但其实没有做到对隐私的保护。
加“密”货币的迷思
现在,让我们来仔细想一下比特币到底用了多少密码学的东西?首先,比特币利用抗碰撞哈希引用来构建区块链的结构,同一个哈希引用不会对应于两个不同的区块;其次,比特币上的每一笔钱都由相应的公钥和私钥控制。除此之外,比特币并没有应用更多的密码学知识了。
因此,我们可以说,比特币的安全性是受到密码学的保护的,但是隐私性其实并没有。我们可以通过很多方式进行分析,例如根据交易的关联性,交易时间和交易的广播情况等,就可以找到账户对应的个人是谁,从而得知这个人在比特币上的交易情况等隐私信息。
Mimblewimble 的目的就是在改善比特币的这一问题。今天我们先来简单介绍一下 Mimblewimble 隐私保护技术的原理,再讲一下它在实际中应用的例子。
“伏地魔”创造的 Mimblewimble
Mimblewimble 其实不是一个传统的英文单词,它源于著名小说《哈利·波特》里“混淆咒”的咒语——施咒的效果是让对方说话变得含混不清,从而丧失念咒语施法的能力。当然,用在区块链里的 Mimblewimble,肯定不是这个咒语的原始意义了,它是指一个在比特币交易中保护用户数据隐私的提案。
这个提案最早以匿名的方式被发布在 Bitcoin 的 IRC Channel 里,作者化名为 Tom Elvis Jedusor,也就是法语版《哈利·波特》里伏地魔的名字。
其实最早提出的 Mimblewimble 方案并不完整,后来经过社区其他人的改进和完善才有了现在的版本。这是一个为基于 output 模型的公有账本提供加密货币隐私性的设计方案,并不涉及共识层,可用在几乎任何共识规则系统上。
跟比特币相比,Mimblewimble 最主要的优势在于信息的隐私性,如交易金额等隐私信息都被密码学技术保护。隐私性带来的一个直接好处,就是交易中的数字资产具有完全的可替换性——例如一些资金可能会被第三方认定为来路不明、甚至标记为赃款,在使用时有被拒收的风险,而收款方为了避免此类风险,就必须承担额外的验证成本。
另一方面,比特币等非匿名数字货币的交易历史是完全透明公开的,如果对每一笔交易的金额和去向进行分析,事实上可以得到很多隐私信息,这也阻碍了它们成为更广泛使用的交易媒介。
其实远在比特币之前,就有一种古老的交易形式可以实现对隐私性非常好的保护:交易双方将钱藏到袖子里达成交易,这样即使其他人目睹了这笔交易,也无法得知交易的金额等隐私信息。但是直接将这样的思路照搬到区块链里并不容易。因为在一个公开的账本里,每一笔交易的合法性需要得到其他人的验证,以确保交易的发起方确实授权了这笔交易,并且这笔交易没有造成恶性通货膨胀。
怎么样能既把一笔交易的具体信息“藏到袖子里”,同时又允许其他人验证交易的合法性呢?这即是 Mimblewimble 所解决的问题。
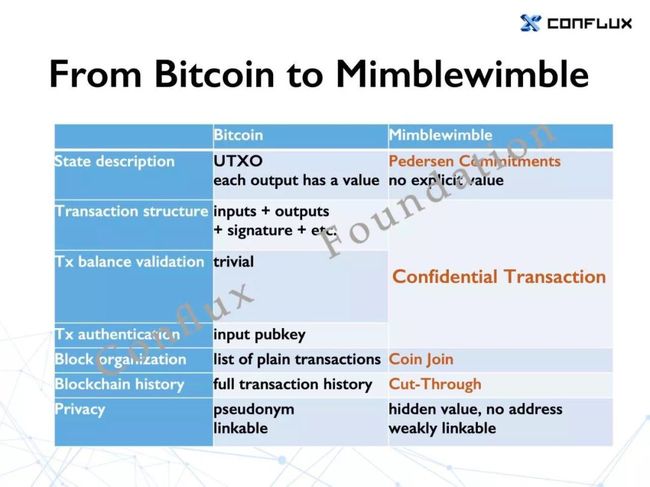
我们先来看大家最熟悉的比特币的设计。众所周知,比特币对交易的隐私性保护得并不是很好:在比特币系统里,尽管每个用户都有一个匿名的钱包地址作为在链上的化名/假名,但每个地址所对应的交易记录与信息在上链后其实都是可以通过公开渠道查询到的。通过将与匿名地址有交易往来的用户的信息进行交叉分析,就可以轻易地追溯到用户的真实身份。
MimbleWimble 三大贡献为改善比特币的隐私性、可替代性和扩容性
最初提出 MimbleWimble 这个方案的目的就是为了给比特币提供隐私性。使用后有以下的好处:
保障隐私性:账户归属和交易关联都会被隐藏,交易金额也会被隐藏起来。这也是 MimbleWimble 最直接的好处。
实现比特币的可替代性:这意味着每笔钱都是同样“干净”的,可互相替代的。比如在比特币中,有些钱可能会被标记为赃款,一旦收到这样的比特币就有无法将它花出去的风险——很多机构都会拒绝接收这样的赃款。有隐私性之后,每一笔钱看不到地址,就有了可替换性,最直接的好处就是收款方不用自己去追踪看收到的钱是不是赃款,会为交易减少很多额外的负担。就像大家平时花人民币通常也不会专门查一下序列号,先检查一下这钱是不是别人从银行抢出去的。
对扩容有一些贡献:这是一个额外的好处。主要是通过裁剪,可以减少状态历史的尺寸,降低存储压力和同步数据的难度。
而 Mimblewimble 主要提高的就是交易的隐私性,使得其他人无法轻易看到哪些用户之间发生了交易,更看不到交易的具体金额是多少。
实际上,Mimblewimble 交易的连接性的保护,是一种比较被动的方式。即大家不会保存所有交易历史,于是就不能直接从网络查询到很久以前的交易记录了。但如果实时地关注每笔交易的动态并且全都记录下来,还是可以得知每笔交易是由哪个用户发给谁的,不过即使如此,交易的金额依然是从始自终都不会公开。
Mimblewimble 所用技术主要有保密交易(Confidential Transaction,也称 CT)、Coin Join 和 Cut-through 等。简单分述如下:
Confidential Transaction 的核心思想是以 Pedersen 承诺方案(Pedersen Commitments)、而非明文的形式存储每个 output 的金额,再通过加法同态的性质验证交易输入输出的金额是合法的;
Coin Join 是在出块时即把整个区块里的所有交易混合成一笔多个 input 到多个 output 的巨大交易,从而使其他人难以追踪每笔 output 资金来源,相对比特币的不可关联性也更好;
Cut-through 技术则是对交易历史进行裁剪,舍弃所有不需要的中间交易数据,最后只留下相当于从 Coinbase 转账到 UTXO 的一笔交易。这样可以极大地缩小整个区块链的历史数据体积,从而减轻存储压力并有利于整个系统扩容,特别有利于新加入的节点快速跟上整条链当前的最新状态。
如果想要深入理解 Mimblewimble 的原理,需要先了解下有关椭圆曲线和 Pedersen 承诺方案的基础知识(有兴趣的读者可以自行查阅相关资料,此处省略五千字)。
简单来说,关于椭圆曲线,我们只需要知道:1)椭圆曲线跟我们高中学的椭圆没有半毛钱关系,99%以上的人到大学毕业也不会学到;2)椭圆曲线上的元素可以进行加法和标量乘法的运算,但是除法运算极其困难——也就是说,给定椭圆曲线的两个点 G 和 H,我们可以很容易地计算出 G+H 或者 233*G 对应于哪个元素,却很难计算 H/G 的值(也即找到一个满足 k*G=H 的整数 k)。椭圆曲线签名实际上也是利用了这个单向的性质。
Pedersen 承诺方案是一种承诺方式,即根据承诺值很难计算出对应的明文,但是如果给出明文则很容易验证它和承诺值是对应的。这点其实跟我们常用的抗碰撞哈希函数有点像。《三国演义》中,周瑜和诸葛亮分别把自己想到的破曹之计写在手心上然后同时摊开的桥段,描写的就是一个线下版本的“承诺-验证”过程。
当然,Pedersen 承诺方案还有一些额外的性质,那就是对于加法的同态性。它会把要承诺的数 v 和一个随机数 r 一起记录成 C=r*G+v*H 的形式,其中 G 和 H 是椭圆曲线群的两个生成元。这样,我们把两个分别关于 (v1,r1) 和 (v2,r2) 的承诺值(按照椭圆曲线的加法)加在一起就可以得到一个关于(v1+v2,r1+r2)的承诺值,并且在这个过程中都不需要知道 v1,v2 的值。
可能说到这儿,大家会觉得太学术了。椭圆曲线到底有什么用呢?其实说到底,椭圆曲线就是为了保障账户的隐私和安全性。举例说来,椭圆曲线就像是一个不透明的袋子,你可以把自己的金子放进这个袋子里,其他人就看不见你到底有多少金子。但是,你可以向别人证明几个袋子加總共有 100 两金子,同时别人卻無法得知每个袋子分别是幾两。
Mimblewimble 的框架和原理
现在,我们从三个方面来介绍一下 Mimblewimble 的框架:首先是每笔 Output 输出是什么样,也就是每笔钱会以怎样的形式存储;其次是每笔交易是什么样,也就是这些 Output 是如何转换的;最后则是如何把交易打包成块,把块链接成整条区块链。
我们先来看一下每笔的 Output 的呈现形式。同比特币中的 UTXO 的一样,Mimblewimble 的 UTXO 也是一个所有未花掉 Output 的列表。区别在于,比特币的 UTXO 列表每一项呈现格式是一个地址对应一个明文金额,而 Mimblewimble 則非如此。Mimblewimble 在这里用了 Pedersen 承诺方案的方式存储每笔 Output 金额,并把其中随机数的部分,作为交易生成签名要用的私有信息。另外,每个 Output 还需要附有一个金额范围的合法性证明,避免出现金额为负数或者溢出的问题。
然后是交易的处理。一笔交易其实就是資金从先前创建的 Output 流动到新创建 Output 里的過程。在 Mimblewimble,每笔交易的输入输出都是以 Pedersen 承诺方案的形式出现,金额都是被隐藏起来的。那么怎么去验证交易的合法性呢?这里其实有两件事需要得到验证:一是同一笔交易的输入与输出金额需要时能对上;二是交易得到了输入资产所有人的授权。
如果有明文的金额信息,第一条是非常容易验证的,只需比较输入的整体金额相加等于输出金额整体加上手续费即可。但是 Mimblewimble 交易中没有出现具体的金额,所以这里是利用了加法同态的性质进行验证。比如说,现在有 C1=r1*G+v1*H 和 C2=r2*G+v2*H 两笔输入以及 C3=r3*G+v3*H 和 C4=r4*G+v4*H 两笔输入,我们只需要验证 (C1+C2)-(C3+C4+fee*H)=k*G 即可。因为只有 v1+v2=v3+v4+fee 的时候 H 前面的系数才能正好抵消掉,只剩下 G 的倍数。
这里的 k*G 被称为 excess value,可以被作为一个公钥,用于验证的这笔交易是经过资产所有人的许可的,也就是需要一个以 k 为私钥的签名来证明交易得到授权。因为 k 实际上是 r1、r2、r3、r4 的一个线性组合,其中 r3 和 r4 是由接收方选取的随机数,所以上述签名实际上需要发送方和接收方合作进行一个以 k 为私钥的多重签名才能完成。交易手续费、excess value、以及对应的签名合在一起,就构成了一笔交易的 kernel,用于辅助验证交易的合法性。
其实,只是上述步骤还不足以保证交易合法。如果输出的金额是负数,实际上就可以凭空地造出一些钱来。比如我把一块钱转到两个账户里,这两个账户分别有正的一万零一块钱和负一万块钱,这样虽然转账前后总金额上是相等的,但实际上我可以抛弃掉金额為负的账户,于是最后的结果就是凭空多出了一笔钱。所以为了解决这个问题,每个输出还必须附带一个范围证明,用于保证输出对应的金额是正的且在某个范围以内。这个证明最初是用环签名做的,缺点是证明比较长,证明范围在 (0,2^64) 大约要 5kB 左右。后来有了 Bulletproof 的零知识证明技术,可以把范围证明的大小缩小到 1kB 以内。
接下来我们说一下如何把交易打包成块。在这里 Mimblewimble 用到了和比特币里面的 Coin Join 混币技术类似的方法,把每个块里所有交易输入输出分别按照顺序排列,组成一个非常大的交易。我们可以很容易通过同态加法的性质,验证这笔新交易的输入输出总金额是否平衡。但很显然,矿工不可能对这笔交易重新做出一个签名。所以每个交易的 kernel 都会被保留下来用于辅助验证。
这里其实还有一点小的 trick,就是如果直接用“excess value=输入 commitment 之和-输出 commitment 之和”的方式存储的话,还是有可能通过 kernel 中 excess value 的值从整个区块的输入输出中找到对应的交易的输入输出的。所以,为了消除这种关联性,Mimblewimble 除了 excess value 以外,还要求每笔交易指定一个 offset,使得“excess value +offset*G=输入 commitment 之和-输出 commitment 之和”。然后在打包区块的时候,可以把整个块里所有交易的 offset 全部加總为一个总的 offset,这个总的 offset 既足以帮助验证区块内交易合法,又可以隐藏个别交易的 offset,消除关联性。
有了单独的区块以后,我们可以把整个区块链历史上所有的区块全都放在一起,再进行一次混合的操作,也就是所谓的 Cut-through。这次操作以后,就可以把所有已经花掉的输出都从交易历史中移除——因为它们会作为输入输出各出现一次,对于验证金额来说正好可以抵消掉。当然,移除输出的同时也可以移除它们对应的范围证明,这就省下来了很多空间。
经过这样的裁剪后,输入端只剩下 Coinbase 发币的输入,这实际上可以从当前块的高度直接算出来,不需要存储;输出端剩下的恰好是所有还没有被花掉的输出,也即通常所说的 UTXO。于是整个区块链的历史就可以不再存储那些已被花掉的输出了。为了验证这个从 Coinbase 输入到 UTXO 的交易的合法性,所有历史交易的 kernel 依然有必要保留,不过 kernel 的尺寸比起每笔交易来还是要节省不少的。
Mimblewimble 在扩容性上的意义
比特币目前有接近 4 亿笔的交易,但是 UTXO 里大约只有 6000 多万个 Output。新用户若想加入比特币网络,就得先知道過去所有的 200+GB 挖矿历史,才能验证最新的块。而如果应用 Mimblewimble 的方式,区块链的交易历史会被舍弃,只留下大约 25GB 的历史交易 kernel,這樣处理数据时的复杂度即会减少很多。当然,Mimblewimble 的 UTXO 需要附带每个输出的范围证明,这是一个额外的负担,但是这个负担仅与 UTXO 的大小有关,而与整个链已经运行的时间无关。此外,采用了新的 Bulletproof 技术后,范围证明的尺寸和验证效率都有了很大的改进。
Mimblewimble 在实际项目中的应用
在 2018 年底和 2019 年初有 Grin 和 Beam 两个基于 Mimblewimble 的项目先后上线。它们都为交易提供了更好的隐私性:没有地址,也不会暴露交易金额,同时也难以把交易关联起来。两个项目都采用了 Bulletproof 技术用于范围证明。此外,Grin 还支持多种常用的脚本,Beam 也计划在今年实现对于常见脚本的支持,这在原本的 Mimblewimble 协议里是无法实现的,還用到了一些特别的技术。
这两个项目最大的区别在于发币的规则以及开发团队获得报酬的方式: Grin 选择了一个线性的无上限的发行策略,开发团队的报酬完全依赖于用户和矿工们的捐赠;Beam 采用了更接近于比特币的有上限且固定周期减半的发行策略,开发团队靠著從前五年的挖矿奖励中抽成來获得收益。
我们来看看他俩的一个简单对比:
首先,他们都通过 MimbleWimble 获得了对于隐私性的保护。
其次,他们都采用了 Bulletproof 做范围证明。
对于脚本和合约的支持方面:Grin 实现了多重签名,闪电网络等。注意,MimbleWimble 只能验证交易不能验证合约。
Beam 不支持合约,但他们计划要做。
网络层广播:Grin 和 Beam 交易信息看不出,但是广播层能直接看到 IP,依然可以得到隐私信息。通过加密再转发,无人知道交易是谁转出的。
Beam 还实现了 SBBS:这个只有 Mimblewible 需要做。因为 MimbleWimble 中的每笔交易需要双方一起签名。一方可以把签了一半的东西,放在这个安全的 bbs 上,另一个人下载后再去签名,最后把交易发出去。这样的好处是不需要双方同时在线。
pow 的区别:Grin 使用的是 Cuckoo cycle 的变种,而 Beam 是 Equihash
Grin 发币是线性的, 所以会一直通胀
Beam:过段时间会减半,发币总量有上限
Grin Foundation 是靠 donation 运营。之前捐款没达到目标,还号召大家快点多捐一点。
Beam 是会从前五年的块里面抽税用于奖励开发者。
Grin 和 Beam 都是 Mimblewimble 技术在加密数字货币的实践中非常好的尝试。尽管它们还有种种不成熟和不足之处,但是这样的尝试必将为未来区块链上的隐私保护提供更多宝贵的、可供借鉴的经验。(本文首发于 DeepTech 平台每周二之 DeepHash 专栏)
杨光
杨光毕业于清华大学姚班,并于清华大学交叉信息研究院获得计算机科学博士学位。加入 Conflux 团队前曾在丹麦奥胡斯大学、中科院计算所、比特大陆从事研究工作。他的研究方向包括密码学、博弈论和区块链。他的博士论文曾获得中国密码学会优秀博士学位论文奖。
-End-
文章转载自DeepTech深科技
![]()