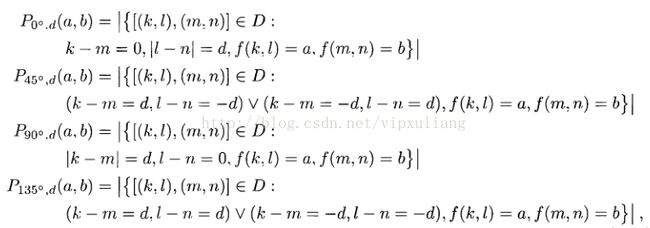利用灰度共生矩阵提取图像纹理特征
利用灰度共生矩阵提取图像纹理特征
--xuliang
1. 灰度共生矩阵概念
灰度共生矩阵定义为像素对的联合概率分布，是一个对称矩阵，它不仅反映图像灰度在相邻的方向、相邻间隔、变化幅度的综合信息，但也反映了相同的灰度级像素之间的位置分布特征，是计算纹理特征的基础。
在图像中任意取一点(x,y)及偏离它的一点(x+a,y+b)(其中，a、b为整数，人为定义)构成点对。设该点对的灰度值为(f1,f2)，再令点(x,y)在整幅图像上移动，则会得到不同的(f1,f2)值。
设图像的最大灰度级为L，则f2与f2的组合共有L*L种。对于整幅图像，统计出每一种(f1,f2)值出现的次数，然后排列成一个方阵，再用(f1,f2)出现的总次数将他们归一化为出现的概率P(f1,f2)，由此产生的矩阵为灰度共生矩阵。θ方向上的间隔为d的灰度共生矩阵实际上是θ方向间隔为d的灰度变化量的联合概率分布。
2. 共生矩阵的计算
（1）
公式(1)中d表示像素间隔，(k,l), (m,n)分别为原像素和偏移后的像素坐标，其中k,m为纵坐标，D为图像范围[Image Processing, Analysis, and Machine Vision (Sonka 3rd Edition2007)]。
举例说明，假设原图像如图1.a所示
1.a 灰度图像 1.b 0°方向距离为1的灰度共生矩阵 1.c P135°,1
对1.b中蓝色字表示原像素灰度值，红字为偏移后像素灰度值。则对矩阵元素P0°,1 (0,0)表示1.a中在0°方向上（包括正和负方向）相距为1的(0,0)点对有两对，考虑正负方向的加倍效果，P0°,1 (0,0)=4。同样由于公式(1)对距离d定义的双向性，使得灰度共生矩阵为对称矩阵。
为了减小计算量，可将d定义为沿θ正方向。则(1)式变为
（2）
由1.a得到的新的灰度共生矩阵为
3. 共生矩阵计算纹理特征
熵(Entropy)：是图像包含信息量的随机性度量。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时，熵最大；因此熵值表明了图像灰度分布的复杂程度，熵值越大，图像越复杂。
（4）
最大概率(Maximum probability)：表示图像中出现次数最多的纹理特征。
（5）
对比度(Contrast)：度量矩阵的值是如何分布和图像中局部变化的多少，反应了图像的清晰度和纹理的沟纹深浅。纹理的沟纹越深，反差越大，效果清晰；反之，对比值小，则沟纹浅，效果模糊。对公式(6)，典型的有κ=2，λ=1。
倒数差分矩(Inverse difference moment)：反映图像纹理的同质性，度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化，局部非常均匀。
（7）
相关性(Correlation)：自相关反应了图像纹理的一致性。如果图像中有水平方向纹理，则水平方向共生矩阵Correlation值大于其余方向共生矩阵Correlation的值。它度量空间灰度共生矩阵元素在行或列方向上的相似程度，因此，相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时，相关值就大;相反，如果矩阵像元值相差很大则相关值小。
（8）
其中μx, μy为均值，σx, σy为标准差，计算公式如下
4. 算法实现
GLCM.h
#include
enum GLCMdirEnum
{
horizonal = 1,//0°
vertical = 2,//90°
diagonal = 3,//45°
antidiagonal = 4//135°
};
class GLCM
{
private:
unsigned int** GLCMdata;
unsigned char* imageData;
int imageWidth,imageWidthStep,imageHeight,imageDepth,GLCMheight;
public:
unsigned int GLCMenergy,GLCMcontrast,GLCMmaxprobability,GLCMstdeviation;
double GLCMentropy,GLCMIDM,GLCMcorrelation;
int getImage(IplImage* pimg);
int calImageGLCM(GLCMdirEnum direction,int distance,int newgraydepth);
int initGLCM(int newgraydepth);
int releaseGLCM();
int printGLCM();
}; GLCM.cpp
#include "GLCM.h"
#include
using namespace cv;
using namespace std;
int GLCM::getImage(IplImage* pimg)
{
if (!(pimg->imageData))
{
return -1;
}
imageData = (unsigned char*)pimg->imageData;
imageDepth = pimg->depth;
imageWidth = pimg->width;
imageWidthStep = pimg->widthStep;
imageHeight = pimg->height;
return 0;
}
int GLCM::calImageGLCM(GLCMdirEnum direction,int distance,int newgraydepth)
{
if (direction>4||direction<1)
{
cout<<"entry a direction value between 1 to 4"<imageDepth||newgraydepth<1)
{
cout<<"entry a bitdepth value between 1 to origin image bitdepth"<0)
{
GLCMenergy += GLCMdata[imatsize][jmatsize] * GLCMdata[imatsize][jmatsize];//能量
GLCMcontrast += (imatsize-jmatsize)*(imatsize-jmatsize)*GLCMdata[imatsize][jmatsize];//对比度
GLCMmaxprobability = GLCMmaxprobability > GLCMdata[imatsize][jmatsize] ? GLCMmaxprobability : GLCMdata[imatsize][jmatsize];//最大概率
GLCMentropy += static_cast(GLCMdata[imatsize][jmatsize]) * std::log(GLCMdata[imatsize][jmatsize]);
if (imatsize!=jmatsize)
{
GLCMIDM += static_cast(GLCMdata[imatsize][jmatsize])/((imatsize-jmatsize)*(imatsize-jmatsize));
}
}
}
}
return 0;
}
int GLCM::initGLCM(int newgraydepth)
{//初始化灰度共生矩阵，若要输出8*8矩阵，newgraydepth输入3,16*16则newgraydepth为4
GLCMheight = std::pow(2,newgraydepth);
GLCMdata = new unsigned int*[GLCMheight];
for (int imat=0;imat 主函数testGLCM.cpp
#include
#include "GLCM.h"
using namespace std;
using namespace cv;
int main()
{
IplImage* img = cvLoadImage("texture7.jpg",CV_LOAD_IMAGE_GRAYSCALE);
GLCM glcm1;
glcm1.getImage(img);
GLCMdirEnum d = horizonal;
glcm1.calImageGLCM(d,1,3);
glcm1.printGLCM();
glcm1.releaseGLCM();
return 0;
} 5. 结果与分析
测试用图
图2. 测试用图(a) (b)
本程序执行结果与MATLAB对比：
3.a
3.b
计算图2(a)的GLCM，结果如图3.a为本程序执行结果，3.b为MATLAB的graycomatrix函数执行结果。两者有细微差异，原因是MATLAB在将图像从256级灰度重新量化至8级灰度时计算方法略有不同，具体参考graycomatrix.m第173行。
不同图片计算GLCM：
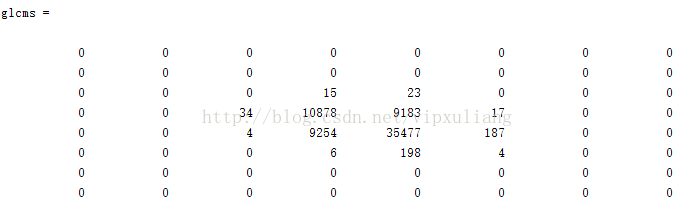
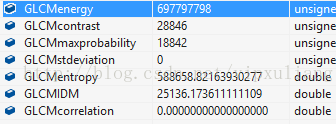
对图2(a)与2(b)计算GLCM的结果，得到矩阵及纹理特征值分别如下（为0的两项未计算）。
图2(a)的GLCM及特征值
图2(b)的GLCM及特征值
文章代码打包至http://download.csdn.net/detail/vipxuliang/7658437 下载