GMRES方法求解二维不可压Stokes方程(附MATLAB代码)
目录
一、问题描述
二、 问题分析
三、 数值格式
四、 数值实验
GMRES方法
预处理的GMRES方法
数值解图像
一、问题描述
通常设 ![]() 令
令 ![]()
定义流函数 ![]() 满足
满足
x相应的边界条件为
之后利用有限差分来计算.
问题:
1. 写出离散格式对应的代数系统, 即 ![]() ;
;
2. 设计有效的迭代法求解 ![]() 要求单步迭代的复杂度为
要求单步迭代的复杂度为 ![]() 其中
其中 ![]() 为
为 ![]() 的维数;
的维数;
3. 设计有效的预条件, 并比较预处理前后迭代法的效率差别.
二、 问题分析
在[0,1]上进行等距差分,![]() 记
记![]() 其中
其中![]()
在![]() 点处, 有:
点处, 有:
若![]() 是内点, 即
是内点, 即![]() 离散方程为
离散方程为
若 ![]() 是边界点, 以
是边界点, 以 ![]() 为例
为例
其余边界点类似, 即
对于角点
三、 数值格式
由第二部分的问题分析可知, 此问题对应的数值格式为![]() 其中
其中
![]()
故可知![]()
其中![]() 具体来说,考虑
具体来说,考虑![]() 的元素, 经过分析易知, 这等价于
的元素, 经过分析易知, 这等价于![]() 在区间
在区间![]() 上的离散, 即有
上的离散, 即有
经分析有
![]()
类似的办法来处理![]() 和
和![]() 有
有![]() 为
为![]() 在
在![]() 上的离散,
上的离散, ![]() 为
为![]() 在
在![]() 上的离散. 即
上的离散. 即
类似有
至此,我们便得到了离散的数值格式.
由图可知,![]() 是不对称的稀疏矩阵, 故我们用GMRES算法和预优GMRES算法来求解此问题.
是不对称的稀疏矩阵, 故我们用GMRES算法和预优GMRES算法来求解此问题.
四、 数值实验
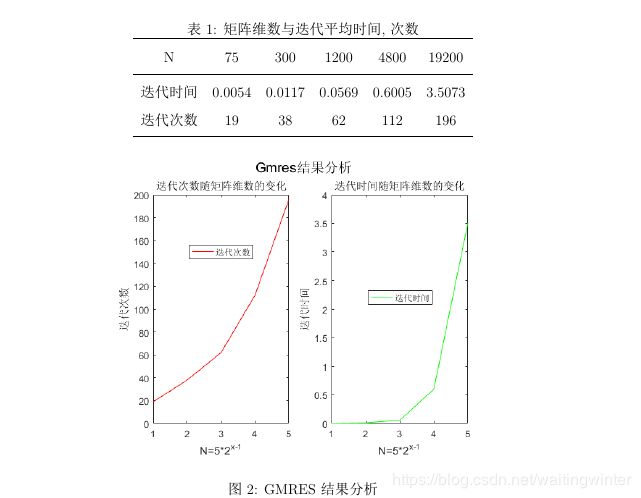
GMRES方法
我们取[0,1]上的分隔点为5,10,20,40,80, 对应的矩阵![]() 维数为
维数为 ![]()
GMRES的MATLAB代码为
function [ x,j,res,resvec,time] = mygmres( A, b, x0, tol, max_it )
%% GMRES METHOD
% j : the number of iterations;
% res : the residual value at termination;
% x : solution
% time : CPU time;
if nargin < 5
max_it=1000;
end
if nargin < 4
tol = 1.e-10;
end
if nargin < 3
x0 = zeros(length(b),1);
end
tic;
r0 = A*x0 - b;
beta = norm(r0);
V(:,1) = r0/beta;
resvec = beta;
Q = cast(1,'like',b);
j = 0;
while ((abs(resvec(j + 1)) > tol) && (j < max_it))
% Arnoldi %
j = j + 1;
w = A*V(:,j);
for i = 1:j
H(i,j) = w'*V(:,i);
w = w - H(i,j)*V(:,i);
end
H((j + 1),j) = norm(w,2);
V(:,(j + 1)) = w/H((j + 1),j);
% Construct R and Givens rotation %
H(1:j,j) = Q*H(1:j,j);
rho = H(j,j);
H(j,j) = sqrt(rho^2 + H((j +1),j)^2);
c = rho/H(j,j);
s = H((j + 1),j)/H(j,j);
H((j + 1),j) = 0;
% Apply Givens rotation to Q %
Q((j + 1),:) = -s*Q(j,:);
Q(j,:) = c*Q(j,:);
Q((j + 1),(j + 1)) = c;
Q(j,(j + 1)) = s;
% Apply Givens rotation to resvec%
resvec(j + 1,1) = -s*resvec(j,1);
resvec(j,1) = c*resvec(j,1);
end
y = H((1:j),:)\resvec(1:j);
x = x0 - V(:,(1:j))*y;
res = abs(resvec(j + 1));
resvec = abs(resvec);
time=toc;
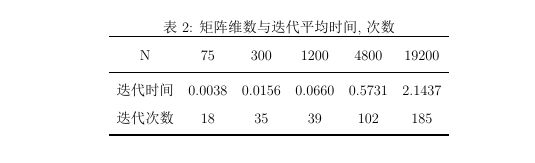
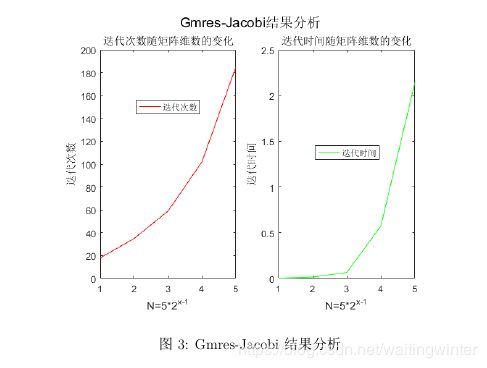
end预处理的GMRES方法
同样,取预处理矩阵为Jacobi矩阵,即
M = diag(diag(A));有
比较两种方法, 我们有
其中, 预优GMRES方法为
function [ x,j,res,resvec,time] = mygmres_ja( A, b, x0, tol, max_it )
%% GMRES METHOD (Pre-processing M = Jacobi)
% j : the number of iterations;
% res : the residual value at termination;
% x : solution
% time : CPU time;
if nargin < 5
max_it=1000;
end
if nargin < 4
tol = 1.e-10;
end
if nargin < 3
x0 = zeros(length(b),1);
end
tic;
M = diag(diag(A)); % Jacobi pre-processing matrix;
r0 =M\(A*x0 - b);
beta = norm(r0);
V(:,1) = r0/beta;
resvec = beta;
Q = cast(1,'like',b);
j = 0;
while ((abs(resvec(j + 1)) > tol) && (j < max_it))
% Arnoldi %
j = j + 1;
w = M\A*V(:,j);
for i = 1:j
H(i,j) = w'*V(:,i);
w = w - H(i,j)*V(:,i);
end
H((j + 1),j) = norm(w,2);
V(:,(j + 1)) = w/H((j + 1),j);
% Construct R and Givens rotation %
H(1:j,j) = Q*H(1:j,j);
rho = H(j,j);
H(j,j) = sqrt(rho^2 + H((j +1),j)^2);
c = rho/H(j,j);
s = H((j + 1),j)/H(j,j);
H((j + 1),j) = 0;
% Apply Givens rotation to Q %
Q((j + 1),:) = -s*Q(j,:);
Q(j,:) = c*Q(j,:);
Q((j + 1),(j + 1)) = c;
Q(j,(j + 1)) = s;
% Apply Givens rotation to resvec%
resvec(j + 1,1) = -s*resvec(j,1);
resvec(j,1) = c*resvec(j,1);
end
y = H((1:j),:)\resvec(1:j);
x = x0 - V(:,(1:j))*y;
res = abs(resvec(j + 1));
resvec = abs(resvec);
time=toc;
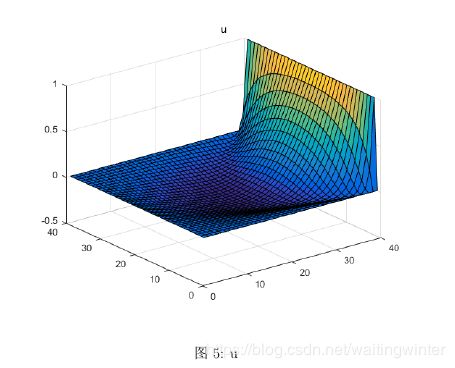
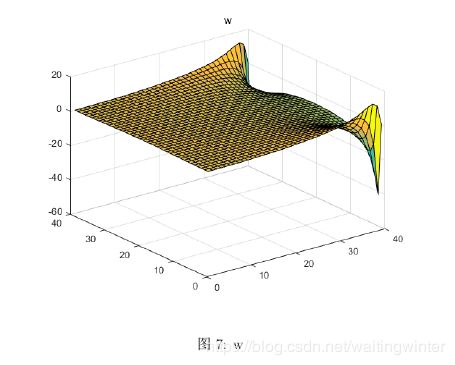
end数值解图像
最后, 我们给出最终的数值解图像
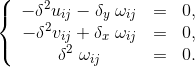
![A=\left[\begin{array}{ccc} A_{11}&A_{12}&A_{13}\\ A_{21}&A_{22}&A_{23}\\ A_{31}&A_{32}&A_{33} \end{array}\right],](http://img.e-com-net.com/image/info8/c6ba20c68f4548d6b1577867a57391d8.gif)