通常这类问题希望我们要“投机取巧”,即先找店家或他人借空瓶,换酒喝完后再如数归还
为求全面,本人分别对“允许借空瓶”与“不允许借空瓶”两种情况进行推导
(一)允许借空瓶:
能借到空瓶我们可以尽可能做到物尽其用
每换一次需要a个空瓶,而换来的酒喝完后又有b个空瓶,实际每次兑换空瓶减少(a-b)个
于是n个空瓶总共可兑换:n/(a-b) 次(式中除法为整数除法,商为兑换次数,余数则是最后剩余的空瓶数)
由于每次兑换可得到b瓶啤酒,于是共可兑换n/(a-b)*b瓶啤酒
一共能喝到的啤酒数当然也就为(n + n/(a-b)*b)瓶了
(二)不允许借空瓶
如果没人愿意借给你空瓶,此时只能“自力更生”了
若n小于a,很明显一次也兑换不了,一共能喝的也就是买的那n瓶啤酒
若n不小于a,一旦剩余空瓶数小于a,则兑换结束
为方便计算,预留a个空瓶,先兑换其余(n-a)个空瓶,于是可从预留的a个空瓶里去“借”,喝完再“归还”
根据“允许借空瓶”情况公式,(n-a)个空瓶总共可兑换:(n-a)/(a-b) 次(同上,式中除法表示整数除法)
由于预留的a个空瓶最后还可再进行一次兑换,故总兑换总次数为:(n-a)/(a-b)+1,化简后为(n-b)/(a-b) 次
最后预留的a个空瓶换的b瓶啤酒喝完后还会得到b个空瓶,故最后剩余的空瓶数为上式余数加b
由于每次兑换可得到b瓶啤酒,于是共可兑换(n-b)/(a-b)*b瓶啤酒
一共能喝到的啤酒数当然也就为(n + (n-b)/(a-b)*b)瓶了
为将以上公式通用化,当n小于b时,b取值同n
基于上述推导,本人开发了求解“空瓶换酒”问题的Win32应用程序,开发语言C/C++(结合Windows SDK)
程序界面如图:
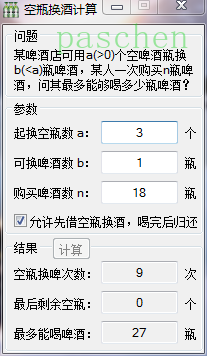
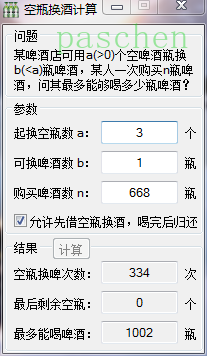
程序主要代码如下:
#include "stdafx.h"
#include
#include
#pragma comment(lib, "Comctl32.lib")
#include
#pragma comment(lib, "Shlwapi.lib")
#define INPUT_LIMIT 9
static HWND hEditA;
static HWND hEditB;
static HWND hEditN;
static HWND hButtonCalc;
static HWND hEditRes1;
static HWND hEditRes2;
static HWND hEditRes3;
static VOID ClearResults()
{
if (!IsWindowEnabled(hButtonCalc))
{
SetWindowText(hEditRes1, TEXT(""));
SetWindowText(hEditRes2, TEXT(""));
SetWindowText(hEditRes3, TEXT(""));
EnableWindow(hButtonCalc, TRUE);
}
}
INT_PTR CALLBACK DialogProc(HWND hWndDlg, UINT uMsg, WPARAM wParam, LPARAM lParam)
{
UNREFERENCED_PARAMETER(lParam);
switch (uMsg)
{
case WM_INITDIALOG:
{
HICON hIcon = LoadIcon(GetModuleHandle(NULL), MAKEINTRESOURCE(IDI_ICON));
SendMessage(hWndDlg, WM_SETICON, ICON_SMALL, (LPARAM)hIcon);
SendMessage(hWndDlg, WM_SETICON, ICON_BIG, (LPARAM)hIcon);
hEditA = GetDlgItem(hWndDlg, IDC_EDIT_A);
hEditB = GetDlgItem(hWndDlg, IDC_EDIT_B);
hEditN = GetDlgItem(hWndDlg, IDC_EDIT_N);
HWND hCheckBorrow = GetDlgItem(hWndDlg, IDC_CHECK_BORROW);
hButtonCalc = GetDlgItem(hWndDlg, IDC_BUTTON_CALC);
hEditRes1 = GetDlgItem(hWndDlg, IDC_EDIT_RES1);
hEditRes2 = GetDlgItem(hWndDlg, IDC_EDIT_RES2);
hEditRes3 = GetDlgItem(hWndDlg, IDC_EDIT_RES3);
SetWindowText(hEditA, TEXT("3"));
SendMessage(hEditA, EM_SETLIMITTEXT, (WPARAM)INPUT_LIMIT, (LPARAM)0);
SetWindowText(hEditB, TEXT("1"));
SendMessage(hEditB, EM_SETLIMITTEXT, (WPARAM)INPUT_LIMIT, (LPARAM)0);
SetWindowText(hEditN, TEXT("18"));
SendMessage(hEditN, EM_SETLIMITTEXT, (WPARAM)INPUT_LIMIT, (LPARAM)0);
SendMessage(hCheckBorrow, BM_SETCHECK, (WPARAM)BST_CHECKED, (LPARAM)0);
return (INT_PTR)TRUE;
}
break;
case WM_COMMAND:
{
switch (wParam)
{
case MAKEWPARAM(IDCANCEL, BN_CLICKED):
{
EndDialog(hWndDlg, (INT_PTR)0);
return (INT_PTR)TRUE;
}
break;
case MAKEWPARAM(IDC_EDIT_A, EN_CHANGE):
{
ClearResults();
return (INT_PTR)TRUE;
}
break;
case MAKEWPARAM(IDC_EDIT_B, EN_CHANGE):
{
ClearResults();
return (INT_PTR)TRUE;
}
break;
case MAKEWPARAM(IDC_EDIT_N, EN_CHANGE):
{
ClearResults();
return (INT_PTR)TRUE;
}
break;
case MAKEWPARAM(IDC_CHECK_BORROW, BN_CLICKED):
{
ClearResults();
return (INT_PTR)TRUE;
}
break;
case MAKEWPARAM(IDC_BUTTON_CALC, BN_CLICKED): //计算部分
{
if (GetWindowTextLength(hEditA) <= 0)
{
MessageBox(hWndDlg, TEXT("未输入起换空瓶数(a)!"), TEXT("错误"), MB_OK | MB_ICONHAND);
SetFocus(hEditA);
return (INT_PTR)TRUE;
}
if (GetWindowTextLength(hEditB) <= 0)
{
MessageBox(hWndDlg, TEXT("未输入可换啤酒数(b)!"), TEXT("错误"), MB_OK | MB_ICONHAND);
SetFocus(hEditB);
return (INT_PTR)TRUE;
}
if (GetWindowTextLength(hEditN) <= 0)
{
MessageBox(hWndDlg, TEXT("未输入购买啤酒数(n)!"), TEXT("错误"), MB_OK | MB_ICONHAND);
SetFocus(hEditN);
return (INT_PTR)TRUE;
}
UINT a = GetDlgItemInt(hWndDlg, IDC_EDIT_A, NULL, FALSE);
if (!a)
{
MessageBox(hWndDlg, TEXT("起换空瓶数(a)应大于0!"), TEXT("错误"), MB_OK | MB_ICONHAND);
SendMessage(hEditA, EM_SETSEL, (WPARAM)0, (LPARAM)-1);
SetFocus(hEditA);
return (INT_PTR)TRUE;
}
UINT b = GetDlgItemInt(hWndDlg, IDC_EDIT_B, NULL, FALSE);
if (b >= a)
{
MessageBox(hWndDlg, TEXT("可换啤酒数(b)应小于起换空瓶数(a)!"), TEXT("错误"), MB_OK | MB_ICONHAND);
SendMessage(hEditB, EM_SETSEL, (WPARAM)0, (LPARAM)-1);
SetFocus(hEditB);
return (INT_PTR)TRUE;
}
UINT n = GetDlgItemInt(hWndDlg, IDC_EDIT_N, NULL, FALSE);
UINT u1, u2, u3;
if (IsDlgButtonChecked(hWndDlg, IDC_CHECK_BORROW) == BST_UNCHECKED)
{
if (n < b)
b = n;
u1 = (n - b) / (a - b);
u2 = (n - b) % (a - b);
u3 = b;
}
else
{
u1 = n / (a - b);
u2 = n % (a - b);
u3 = 0U;
}
TCHAR szText[12];
wnsprintf(szText, 12, TEXT("%u"), u1);
SetWindowText(hEditRes1, szText);
wnsprintf(szText, 12, TEXT("%u"), u2 + u3);
SetWindowText(hEditRes2, szText);
wnsprintf(szText, 12, TEXT("%u"), n + u1 * b);
SetWindowText(hEditRes3, szText);
EnableWindow(hButtonCalc, FALSE);
return (INT_PTR)TRUE;
}
break;
}
}
break;
}
return (INT_PTR)FALSE;
}
extern "C" VOID Startup()
{
{
INITCOMMONCONTROLSEX InitCtrls;
InitCtrls.dwSize = (DWORD)sizeof(INITCOMMONCONTROLSEX);
InitCtrls.dwICC = ICC_WIN95_CLASSES;
InitCommonControlsEx(&InitCtrls);
}
ExitProcess((UINT)DialogBoxParam(NULL, MAKEINTRESOURCE(IDD_DIALOG), NULL, DialogProc, (LPARAM)0));
}
完整的代码及程序下载:点击打开链接
结论
1、将“空瓶换酒”问题公式化,分别推导了“允许借空瓶”与“不允许借空瓶”两种情况计算公式
2、根据推导的计算公式开发了计算“空瓶换酒”问题的程序,比使用循环方式计算的程序简洁且高效
3、通过推导与观察可发现,购买n瓶啤酒大约可以喝到a/(a-b)*n瓶,也就是约为购买数量的a/(a-b)倍(注:这里不再是整数除法),且a越大或a与b越接近时此倍数越大。即使按常见的3:1比例兑换,买668瓶就能喝到1000瓶,一般人是该满意了哈~

