二叉树知识点回忆以及整理
目录
- 二叉树
- 二叉排序树
- 二叉树节点定义
- 创建二叉树
- 二叉树的遍历
- 二叉树节点删除
- 测试代码
- 二叉树的深度
- 二叉树的宽度
- 二叉树某层中的节点数
- 二叉树的叶子节点个数
- 二叉树的最大距离(二叉树的直径)
- 二叉树中某个节点到根节点的路径
- 二叉树中两个节点最近的公共父节点
- 二叉树中两个节点之间的路径
- 翻转二叉树
- 完全二叉树
- 判断二叉树是否满二叉树
- 平衡二叉树
二叉树
在计算机科学中,二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”,左子树和右子树同时也是二叉树。二叉树的子树有左右之分,并且次序不能任意颠倒。
二叉排序树
二叉排序树,又称二叉查找树、二叉搜索树、B树。
二叉排序树是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树。
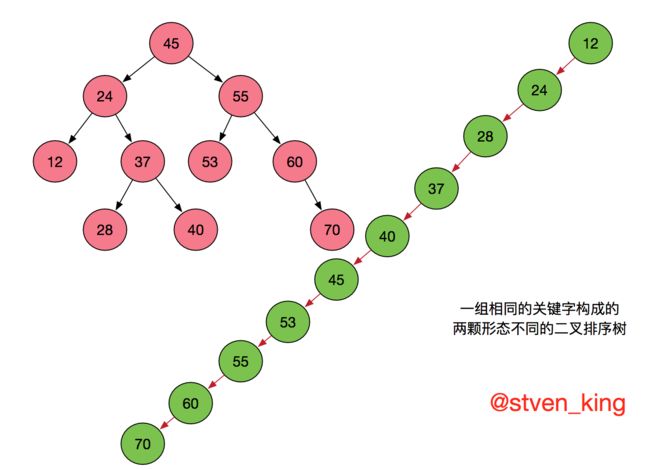
也就是说,二叉排序树中,左子树都比节点小,右子树都比节点大,递归定义。
根据二叉排序树这个特点我们可以知道,二叉排序树的中序遍历一定是从小到大的,比如上图,中序遍历结果是:1 3 4 6 7 8 13 14 19
二叉树节点定义
采用单项链表的形式,只从根节点指向孩子节点,子节点不保存父节点。
/**
* 二叉树节点
*/
class BinaryTreeNode<T> {
T value;
BinaryTreeNode leftNode;
BinaryTreeNode rightNode;
}
创建二叉树
二叉树中左右节点值本身没有大小之分,所以如果要创建二叉树,就需要考虑如何处理某个节点是左节点还是右节点,如何终止某个子树而切换到另一个子树。 因此我选择了二叉排序树,二叉排序树中对于左右节点有明确的要求,程序可以自动根据键值大小自动选择是左节点还是右节点。
/**
* 创建二叉树
*/
public static BinaryTreeNode<Integer> createTreeWithValues(int[] values) {
BinaryTreeNode root = null;
for (int value: values) {
root = addTreeNode(root, value);//添加每一个节点
}
return root;
}
/**
* 在treeNode中添加值为value的节点
*/
public static BinaryTreeNode<Integer> addTreeNode(BinaryTreeNode<Integer> treeNode, int value) {
if (treeNode == null) {
treeNode = new BinaryTreeNode<>();//创建节点
treeNode.value = value;
} else {
if (value <= treeNode.value) {//对比左右节点
treeNode.leftNode = addTreeNode(treeNode.leftNode, value);
} else {
treeNode.rightNode = addTreeNode(treeNode.rightNode, value);
}
}
return treeNode;
}
二叉树的遍历
根据二叉排序树的定义,我们可以知道在查找某个元素时:
- 先比较它与根节点,相等就返回;或者根节点为空,说明树为空,也返回;
- 如果它比根节点小,就从根的左子树里进行递归查找;
- 如果它比根节点大,就从根的右子树里进行递归查找。
这就是一个简单的二分查找。只不过和二分查找还是有些不同的地方的。
二叉树的性能取决于二叉树的层数:
- 最好的情况是O(logn),存在于完全二叉树情况下,其访问性能近似于折半查找;
- 最差的情况是O(n),比如插入的元素所有节点都没有左子树(右子树),这种情况需要将二叉树的全部节点遍历一次。
/**
* 中根遍历
*/
public static void inOrderTraverseTree(BinaryTreeNode<Integer> rootNode) {
if (rootNode != null) {
//左中右,中根遍历
inOrderTraverseTree(rootNode.leftNode);
//中左右,先根遍历
System.out.println(" " + rootNode.value + " ");
//左右中,后根遍历
inOrderTraverseTree(rootNode.rightNode);
}
}
这是一断中根遍历的代码,先根遍历和后根遍历只是调整上面几行代码的顺序而已。
二叉树节点删除
插入操作和查找比较类似,而删除则相对复杂一点,需要根据删除节点的情况分类来对待:
- 如果要删除的节点正好是叶子节点,直接删除就 Ok 了;
- 如果要删除的节点还有子节点,就需要建立父节点和子节点的关系:
- 如果只有左孩子或者右孩子,直接把这个孩子上移放到要删除的位置就好了;
- 如果有两个孩子,就需要选一个合适的孩子节点作为新的根节点,该节点称为 继承节点。(新节点要求比所有左子树要大、比右子树要小,我们可以选择左子树中的最大节点,或者选择右子树中的最小的节点。)
/**
* 二叉树查找
*/
public static BinaryTreeNode<Integer> search(BinaryTreeNode<Integer> rootNode, int value) {
if (rootNode != null) {
if (rootNode.value == value){
return rootNode;
}
if (value > rootNode.value) {
return search(rootNode.rightNode, value);
} else {
return search(rootNode.leftNode, value);
}
}
return rootNode;
}
/**
* 寻找value节点的父节点
*/
public static BinaryTreeNode<Integer> searchParent(BinaryTreeNode<Integer> rootNode, int value) {
//如果当前节点为null,或者当前节点为根节点。返回null
if (rootNode == null || rootNode.value == value) {
return null;
} else {
//当前节点的左儿子或者右儿子等于value,则返回当前节点。
if (rootNode.leftNode != null && value == (Integer)rootNode.leftNode.value ||
rootNode.rightNode != null && value == (Integer)rootNode.rightNode.value) {
return rootNode;
}
//判断需要寻找的节点的位置,
if (value > rootNode.value && rootNode.rightNode != null) {
return searchParent(rootNode.rightNode, value);
} else {
return searchParent(rootNode.leftNode, value);
}
}
}
/**
* 删除rootNode为根节点的二叉树中值为value的节点
*/
public static BinaryTreeNode<Integer> delete(BinaryTreeNode<Integer> rootNode, int value) {
//判断是否删除的节点为根节点
if (rootNode == null && rootNode.value == value) {
rootNode = null;
return rootNode;
}
//找到删除的节点的父节点
BinaryTreeNode<Integer> parentNode = searchParent(rootNode, value);
//找不到父节点,表示该二叉树没有对应的节点
if (parentNode == null) {
return rootNode;
}
BinaryTreeNode<Integer> deleteNode = search(rootNode, value);
//找不到该节点
if (deleteNode == null) {
return rootNode;
}
//需要删除的节点,为叶子节点
if (deleteNode.leftNode == null && deleteNode.rightNode == null) {
deleteNode = null;
if (parentNode.leftNode != null && value == (Integer)parentNode.leftNode.value) {
parentNode.leftNode = null;
} else {
parentNode.rightNode = null;
}
}
//需要删除的节点,只有左子树,左子树继承该删除的位置
else if (deleteNode.rightNode == null) {
if (parentNode.leftNode != null && value == (Integer)parentNode.leftNode.value) {
parentNode.leftNode = deleteNode.leftNode;
} else {
parentNode.rightNode = deleteNode.leftNode;
}
}
//需要删除的节点,只有右子树,右子树继承该删除的位置
else if (deleteNode.leftNode == null) {
if (parentNode.leftNode != null && value == (Integer)parentNode.leftNode.value) {
parentNode.leftNode = deleteNode.rightNode;
} else {
parentNode.rightNode = deleteNode.rightNode;
}
}
//要删除的节点既有左海子,又有右孩子。需要选择一个设施的节点继承,我们选择左子树中的最右节点
else {
BinaryTreeNode<Integer> tmpDeleteNode = deleteNode;
BinaryTreeNode<Integer> selectNode = tmpDeleteNode.leftNode;
if (selectNode.rightNode == null) {
selectNode.rightNode = deleteNode.rightNode;
} else {
//找到deleteNode的左子树中的最右节点,即最大节点
while (selectNode.rightNode != null) {
tmpDeleteNode = selectNode;
selectNode = selectNode.rightNode;
}
//将选出的继承节点的左子树赋值给父节点的右子树
tmpDeleteNode.rightNode = selectNode.leftNode;
//继承节点继承需要删除的左右子树
selectNode.leftNode = deleteNode.leftNode;
selectNode.rightNode = deleteNode.rightNode;
}
//将选出的继承节点进行继承(删除对应节点)
if (parentNode.leftNode != null && value == (Integer)parentNode.leftNode.value) {
parentNode.leftNode = selectNode;
} else {
parentNode.rightNode = selectNode;
}
}
return rootNode;
}
测试代码
public static void main(String[] args) {
int[] array = new int[]{8,3,19,1,6,14,4,7};
//创建二叉树
BinaryTreeNode root = createTreeWithValues(array);
//中根遍历
inOrderTraverseTree(root);
System.out.println();
//插入13
addTreeNode(root, 13);
//中根遍历
inOrderTraverseTree(root);
//删除value=3的节点
delete(root, 3);
System.out.println();
//中跟遍历结果
inOrderTraverseTree(root);
}
结果:
1 3 4 6 7 8 14 19
1 3 4 6 7 8 13 14 19
1 4 6 7 8 13 14 19
Process finished with exit code 0
二叉树的深度
二叉树深度定义:从根节点到叶子节点依次进过的节点形成树的一条路径,最长路径的长度为树的深度。
- 如果根节点为空,则深度为0;
- 如果左右节点都为空,则深度为1;
- 递归思想:二叉树的深度=max(左子树的深度,右子树的深度) + 1;
/**
* 二叉树的深度
*/
public static int depthOfTree(BinaryTreeNode<Integer> root) {
if (root == null) {
return 0;
}
if (root.leftNode == null && root.rightNode == null) {
return 1;
}
int leftDepth = depthOfTree(root.leftNode);
int rightDepth = depthOfTree(root.rightNode);
return Math.max(leftDepth, rightDepth) + 1;
}
二叉树的宽度
/**
* 二叉树的宽度:各层节点数的最大值
* @param root 二叉树的根节点
* @return 二叉树的宽度
*/
public static int widthOfTree(BinaryTreeNode<Integer> root) {
if (root == null) {
return 0;
}
//当前二叉树最大宽度=根节点
int maxWith = 1;
int currentWidth = 0;
//队列:先进先出,每次循环后保留一层树的某一层的所有节点
Queue<BinaryTreeNode<Integer>> list = new LinkedList<>();
list.add(root);
while (list.size() > 0) {
currentWidth = list.size();
//遍历当前层的所有节点,并将所有节点的子节点加入到队列中
for (int i = 0; i < currentWidth; i++) {
BinaryTreeNode<Integer> node = list.peek();
list.poll();
if (node.leftNode != null) {
list.add(node.leftNode);
}
if (node.rightNode != null) {
list.add(node.rightNode);
}
}
maxWith = Math.max(maxWith, list.size());
}
return maxWith;
}
二叉树某层中的节点数
/**
* 二叉树某层中的节点数
* @param rootNode 二叉树根节点
* @param level 层
* @return level层的节点数
*/
public static int numberOfNodesOnLevel(BinaryTreeNode<Integer> rootNode, int level) {
//二叉树不存在,或者level不存在的时候节点数为0
int result = 0;
if (rootNode == null || level < 1) {
return result;
}
//level=1,为根节点,节点数为1
if (level == 1) {
result = 1;
return result;
}
//递归:node为根节点的二叉树的level层节点数 =
// node节点左子树(level - 1)层的节点数 + node节点的右子树(level - 1)层的节点数
return numberOfNodesOnLevel(rootNode.leftNode, level - 1) +
numberOfNodesOnLevel(rootNode.rightNode, level - 1);
}
二叉树的叶子节点个数
/**
* 二叉树的叶子节点个数
* @param rootNode
* @return 叶子节点个数
*/
public static int numberOfLeafsInTree(BinaryTreeNode<Integer> rootNode) {
int result = 0;
if (rootNode == null) {
return result;
}
//rootNode没有子节点,所以根节点为叶节点result=1;
if (null == rootNode.leftNode && null == rootNode.rightNode) {
result = 1;
return result;
}
//递归:root的叶节点 = node的左子树的叶节点 + node的右子树的叶节点
return numberOfLeafsInTree(rootNode.leftNode) + numberOfLeafsInTree(rootNode.rightNode);
}
二叉树的最大距离(二叉树的直径)
二叉树中任意两个节点都有且仅有一条路径,这个路径的长度叫这两个节点的距离。二叉树中所有节点之间的距离的最大值就是二叉树的直径。
有一种解法,把这个最大距离划分了3种情况:
- 这2个节点分别在根节点的左子树和右子树上,他们之间的路径肯定经过根节点,而且他们肯定是根节点左右子树上最远的叶子节点(他们到根节点的距离=左右子树的深度)。
- 这2个节点都在左子树上
- 这2个节点都在右子树上
综上,只要取这3种情况中的最大值,就是二叉树的直径。
**
* 二叉树的最大距离(直径)
* @param rootNode 根节点
* @return 最大距离
*/
public static int maxDistanceOfTree(BinaryTreeNode<Integer> rootNode) {
if (rootNode == null) {
return 0;
}
//1、最远距离经过根节点:距离 = 左子树深度 + 右子树深度
int distance = depthOfTree(rootNode.leftNode) + depthOfTree(rootNode.rightNode);
//2、最远距离在根节点左子树上,即计算左子树最远距离
int disLeft = maxDistanceOfTree(rootNode.leftNode);
//3、最远距离在根节点右子树上,即计算右子树最远距离
int disRight = maxDistanceOfTree(rootNode.rightNode);
return Math.max(distance, Math.max(disLeft, disRight));
}
这个方案效率较低,因为计算子树的深度和最远距离是分开递归的,存在重复递归遍历的情况。其实一次递归,就可以分别计算出深度和最远距离,于是有了第二种方案:
class TreeNodeProperty{
int depth = 0;
int distance = 0;
}
public static int maxDistanceOfTree2(BinaryTreeNode<Integer> rootNode) {
if (rootNode == null) {
return 0;
}
return propertyOfTreeNode(rootNode).distance;
}
public static TreeNodeProperty propertyOfTreeNode(BinaryTreeNode<Integer> rootNode) {
if (rootNode == null) {
return new TreeNodeProperty();
}
TreeNodeProperty left = propertyOfTreeNode(rootNode.leftNode);
TreeNodeProperty right = propertyOfTreeNode(rootNode.rightNode);
TreeNodeProperty p = new TreeNodeProperty();
//当前节点的树的深度depth = 左子树深度 + 右子树深度 + 1;(根节点也占一个depth)
p.depth = Math.max(left.depth, right.depth) + 1;
p.distance = Math.max(Math.max(left.distance, right.distance), left.depth + right.depth);
return p;
}
二叉树中某个节点到根节点的路径
既是寻路问题,又是查找节点问题。
定义一个存放路径的栈(不是队列了,但是还是用可变数组来实现的)
- 压入根节点,再从左子树中查找(递归进行的),如果未找到,再从右子树中查找,如果也未找到,则弹出根节点,再遍历栈中上一个节点。
- 如果找到,则栈中存放的节点就是路径所经过的节点。
/**
* 二叉树中某个节点到根节点的路径
* @param rootNode 根节点
* @param treeNode 节点
* @return 路径队列
*/
public static Stack<BinaryTreeNode> pathOfTreeNode(BinaryTreeNode<Integer> rootNode, int treeNode) {
Stack<BinaryTreeNode> pathList = new Stack<>();
isFoundTreeNode(rootNode, treeNode, pathList);
return pathList;
}
/**
* 查找某个节点是否在树中
* @param rootNode 根节点
* @param treeNode 待查找的节点
* @param path 根节点到待查找节点的路径
* @return 是否找到该节点
*/
public static boolean isFoundTreeNode(BinaryTreeNode<Integer> rootNode, int treeNode,
Stack<BinaryTreeNode> path) {
if (rootNode == null) {
return false;
}
//当前节点就是需要找的节点
if (rootNode.value == treeNode) {
path.add(rootNode);
return true;
}
//将路过的节点压入栈中
path.add(rootNode);
//先在左子树中查找
boolean find = isFoundTreeNode(rootNode.leftNode, treeNode, path);
if (!find) {
//如果没有找到,然后在右子树中查找
find = isFoundTreeNode(rootNode.rightNode, treeNode, path);
}
if (!find) {
path.pop();
}
return find;
}
二叉树中两个节点最近的公共父节点
首先需要明白,根节点肯定是二叉树中任意两个节点的公共父节点(不一定是最近的),因此二叉树中2个节点的最近公共父节点一定在从根节点到这个节点的路径上。因此我们可以先分别找到从根节点到这2个节点的路径,再从这两个路径中找到最近的公共父节点。
/**
* 二叉树种两个节点的最近公共节点
* @param rootNode 根节点
* @param nodeA 第一个节点
* @param nodeB 第二个节点
* @return 最近的公共节点
*/
public static int parentOfNode(BinaryTreeNode<Integer> rootNode, int nodeA, int nodeB) {
if (rootNode == null) {
return -1;
}
//两个节点是同一个节点
if (nodeA == nodeB) {
return nodeA;
}
//其中一个点为根节点
if (rootNode.value == nodeA || rootNode.value == nodeB) {
return rootNode.value;
}
//从根节点到节点A的路径
Stack<BinaryTreeNode> pathA = pathOfTreeNode(rootNode, nodeA);
//从根节点到节点B的路径
Stack<BinaryTreeNode> pathB = pathOfTreeNode(rootNode, nodeB);
//寻找的节点不在树中
if (pathA.size() == 0 || pathB.size() == 0) {
return -1;
}
//将路径的数据结构,变为数组
int[] arrayA = new int[pathA.size()];
int[] arrayB = new int[pathB.size()];
for (int i = pathA.size() - 1; i >= 0; i--){
arrayA[i] = (int) pathA.pop().value;
}
for (int i = pathB.size() - 1; i >= 0; i--) {
arrayB[i] = (int) pathB.pop().value;
}
//第i+1个不相同的节点出现,则第i个节点为最近公共节点
for (int i = 0; i < arrayA.length - 1 && i < arrayB.length - 1; i++) {
if (arrayA[i + 1] != arrayB[i + 1]) {
return arrayA[i];
}
if (i + 1 == arrayA.length - 1) {
return arrayA[arrayA.length - 1];
}
if (i + 1 == arrayB.length - 1) {
return arrayB[arrayB.length - 1];
}
}
return -1;
}
二叉树中两个节点之间的路径
从查找最近公共父节点衍生出来的。
/**
* 二叉树中两个节点之间的路径
* @param rootNode 根节点
* @param nodeA 第一个节点
* @param nodeB 第二个节点
* @return 路径
*/
public static List<Integer> pathFromNode(BinaryTreeNode<Integer> rootNode, int nodeA, int nodeB) {
if (rootNode == null) {
return null;
}
List<Integer> result = new ArrayList<>();
if (nodeA == nodeB) {
result.add(nodeA);
result.add(nodeB);
return result;
}
//从根节点到节点A的路径
Stack<BinaryTreeNode> pathA = pathOfTreeNode(rootNode, nodeA);
//从根节点到节点B的路径
Stack<BinaryTreeNode> pathB = pathOfTreeNode(rootNode, nodeB);
if (rootNode.value == nodeB) {
pathA.forEach(new Consumer<BinaryTreeNode>() {
@Override
public void accept(BinaryTreeNode binaryTreeNode) {
result.add((Integer) binaryTreeNode.value);
}
});
return result;
}
if (rootNode.value == nodeA) {
pathB.forEach(new Consumer<BinaryTreeNode>() {
@Override
public void accept(BinaryTreeNode binaryTreeNode) {
result.add((Integer) binaryTreeNode.value);
}
});
return result;
}
//寻找的节点不在树中
if (pathA.size() == 0 || pathB.size() == 0) {
return null;
}
//将路径的数据结构,变为数组
int[] arrayA = new int[pathA.size()];
int[] arrayB = new int[pathB.size()];
for (int i = pathA.size() - 1; i >= 0; i--){
arrayA[i] = (int) pathA.pop().value;
}
for (int i = pathB.size() - 1; i >= 0; i--) {
arrayB[i] = (int) pathB.pop().value;
}
//第i+1个不相同的节点出现,则第i个节点为最近公共节点
int lastNode = -1;
for (int i = 0; i < arrayA.length - 1 && i < arrayB.length - 1; i++) {
if (arrayA[i + 1] != arrayB[i + 1]) {
lastNode = i;
break;
}
if (i + 1 == arrayA.length - 1) {
lastNode = arrayA.length - 1;
break;
}
if (i + 1 == arrayB.length - 1) {
lastNode = arrayB.length - 1;
break;
}
}
for (int i = arrayA.length - 1; i >= lastNode; i--) {
result.add(arrayA[i]);
}
for (int i = lastNode + 1; i < arrayB.length; i++) {
result.add(arrayB[i]);
}
return result;
}
翻转二叉树
翻转二叉树,又叫求二叉树的镜像,就是把二叉树的左右子树对调(当然是递归的)
/**
* 翻转二叉树
* @param rootNode 根节点
* @return 翻转后的二叉树
*/
public static BinaryTreeNode invertBinaryTree(BinaryTreeNode<Integer> rootNode) {
if (rootNode == null) {
return null;
}
//只有一个根节点
if (rootNode.leftNode == null && rootNode.rightNode == null) {
return rootNode;
}
invertBinaryTree(rootNode.leftNode);
invertBinaryTree(rootNode.rightNode);
BinaryTreeNode tempNode = rootNode.leftNode;
rootNode.leftNode = rootNode.rightNode;
rootNode.rightNode = tempNode;
return rootNode;
}
完全二叉树
A Complete Binary Tree (CBT) is a binary tree in which every level,
except possibly the last, is completely filled, and all nodes
are as far left as possible.
换句话说,完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。
根据《李春葆数据结构教程》书上的完全二叉树定义为:“二叉树中最多只有最下面两层节点的度数小于二,并且最下边的一层的叶子节点都一次排列在该层最左边的位置上,这样的二叉树称为完全二叉树”。
特点
- 叶子节点只可能在层次最大的两层出现;
- 对于最大层次中的叶子节点,都一次排列在该层的最左边的位置上;
- 如果有度为一的叶子节点,只可能有一个,且该节点只有左孩子而无有孩子。
采用优先广度遍历的算法,从上到下,从左到右依次入队列。我们可以设置一个标志位flag,当子树满足完全二叉树时,设置flag=true。当flag=ture而节点又破坏了完全二叉树的条件,那么它就不是完全二叉树。
/**
* 是否完全二叉树
* 完全二叉树:若设二叉树的高度为h,除第h层外,其它各层的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布
* @param rootNode 根节点
* @return 是否是完全二叉树
*/
public static boolean isCompleteBinaryTree(BinaryTreeNode<Integer> rootNode) {
if (rootNode == null) {
return false;
}
//左子树和右子树都是空,则是完全二叉树
if (rootNode.leftNode == null && rootNode.rightNode == null) {
return true;
}
//左子树是空,右子树不是空,则不是完全二叉树
if (rootNode.leftNode == null && rootNode.rightNode != null) {
return false;
}
Deque<BinaryTreeNode<Integer>> queue = new LinkedList<>();
queue.add(rootNode);
//是否满足二叉树
boolean isComplete = false;
while (queue.size() > 0) {
BinaryTreeNode<Integer> node = queue.pop();
//左子树为空且右子树不为空,则不是完全二叉树
if (node.leftNode == null && node.rightNode != null) {
return false;
}
//前面的节点已满足完全二叉树,如果还有孩子节点,则不是完全二叉树
if (isComplete && (node.leftNode != null || node.rightNode != null)) {
return false;
}
//右子树为空,则已经满足完全二叉树
if (node.rightNode == null) {
isComplete = true;
}
//将子节点压入
if (node.leftNode != null) {
queue.add(node.leftNode);
}
if (node.rightNode != null) {
queue.add(node.rightNode);
}
}
return isComplete;
}
判断二叉树是否满二叉树
满二叉树定义为:除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树
满二叉树的一个特性是:叶子数=2^(深度-1),因此我们可以根据这个特性来判断二叉树是否是满二叉树。
/**
* 是否满二叉树
* 满二叉树:除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树
* @param rootNode 根节点
* @return 是否满二叉树
*/
public static boolean isFullBinaryTree(BinaryTreeNode<Integer> rootNode) {
if (rootNode == null) {
return false;
}
int depth = depthOfTree(rootNode);
int leafNum = numberOfLeafsInTree(rootNode);
if (leafNum == Math.pow(2, (depth - 1))) {
return true;
}
return false;
}
平衡二叉树
平衡二叉树定义为:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树又叫AVL树。
/**
* 是否平衡二叉树
* @param rootNode 根节点
* @return 是否平衡二叉树
*/
static int height;
public static boolean isAVLBinaryTree(BinaryTreeNode<Integer> rootNode) {
if (rootNode == null) {
height = 0;
return true;
}
if (rootNode.leftNode == null && rootNode.rightNode == null) {
height = 1;
return true;
}
boolean isAVLLeft = isAVLBinaryTree(rootNode.leftNode);
int heightLeft = height;
boolean isAVLRight = isAVLBinaryTree(rootNode.rightNode);
int heightRight = height;
height = Math.max(heightLeft, heightRight) + 1;
return isAVLLeft && isAVLRight && Math.abs(heightLeft - heightRight) <= 1;
}
本来是想看红黑树的,但关于树相关的知识忘记的差不多了,这几天抽时间看了看二叉树的相关知识,作为笔记整理。
—>>>>>>>>代码
参考文章:
二叉树-你必须要懂!(二叉树相关算法实现-iOS)
文章到这里就全部讲述完啦,若有其他需要交流的可以留言哦!!
想阅读作者的更多文章,可以查看我 个人博客 和公共号:
![]()