线段树入门练习
Powered by:AB_IN 局外人
强推这篇线段树详解,讲的很全面。
戳这!!
- 线段树的构造函数一般有三个
- Build (建树)
- Update(更新值)
- Query(查询值)
- 要开四倍的数组储存数据
tr[maxn<<2] - 如果涉及到区间更新,会用到
- pushup(更新父节点)
- pushdown (涉及到懒标记)
- ADD MUL MAX MIN 等配合pushdown操作的函数,根据题目的具体要求。
- 父节点 i i i的两个子树下标为 : 左 : 2 ∗ i = i < < 1 左: 2*i=i<<1 左:2∗i=i<<1 右 : 2 ∗ i + 1 = i < < 1 ∣ 1 右: 2*i+1=i<<1|1 右:2∗i+1=i<<1∣1
大体知道了这些,再看几遍板子,基本就可以写出属于自己的板子了。
P3372 【模板】线段树 1
带注释的板子。
#include P3373 【模板】线段树 2
秉持先乘后加的原则。
有乘法时,add_tag,mul_tag,tr都得变化,因为乘法优先级大,应该先算乘法,所以之前懒标记 加和乘 的值也得乘上。
#include 小阳的贝壳
一开始看操作一,以为是区间查询和区间修改,但看了2,3操作之后又不知道从何下手。所以采取另一种方案——差分。(b[i]为原数组,a[i]为差分数组)
- 对于操作1,就可用平时维护差分数组的基操。
- 对于操作2,注意是从
l+1开始,因为l+1的差分值是b[l+1]-b[l]。然后维护最大值的绝对值即可。 - 对于操作3,就是我本身不会的知识点——区间gcd。先普及知识:
g c d ( b 1 , b 2 , b 3 , . . . . . . , b n − 2 , b n − 1 , b n ) = g c d ( b 1 , ∣ b 2 − b 1 ∣ , ∣ b 3 − b 2 ∣ , . . . . . . , ∣ b n − 1 − b n − 2 ∣ , ∣ b n − b n − 1 ∣ ) gcd(b_1,b_2,b_3,......,b_{n−2},b_{n−1},b_n)=gcd(b_1,|b_2−b_1|,|b_3−b_2|,......,|b_{n−1}−b_{n−2}|,|b_n−b_{n−1}|) gcd(b1,b2,b3,......,bn−2,bn−1,bn)=gcd(b1,∣b2−b1∣,∣b3−b2∣,......,∣bn−1−bn−2∣,∣bn−bn−1∣)
自然而然,又和差分扯上关系了:
g c d ( b l , b l + 1 , … … , b r ) = g c d ( b l , ∣ b l + 1 − b l ∣ . . . . . . , , ∣ b r − b r − 1 ∣ ) = g c d ( b l , ∣ a l + 1 ∣ , … … , ∣ a r ∣ ) = g c d ( ∑ i = 1 l a i , ∣ a l + 1 ∣ , … … , ∣ a r ∣ ) gcd(b_l,b_{l+1},……,b_r) \\ =gcd(b_l,|b_{l+1}−b_l|......,,|b_r−b_{r−1}|) \\ =gcd(b_l,|a_{l+1}|,……,|a_r|) \\ =gcd(\sum_{i=1}^l a_i,|a_{l+1}|,……,|a_r|) gcd(bl,bl+1,……,br)=gcd(bl,∣bl+1−bl∣......,,∣br−br−1∣)=gcd(bl,∣al+1∣,……,∣ar∣)=gcd(i=1∑lai,∣al+1∣,……,∣ar∣)
ps:第二个等号到第三个等号,是讲差分数组前缀和,就是原数组的值。
所以要维护的有,区间内 a i a_i ai的和,区间内 ∣ a i ∣ |a_i| ∣ai∣的最大公约数,区间内 ∣ a i ∣ |a_i| ∣ai∣ 的最大值,一个单点更新,两个区间查询。
那这有三个,怎么写才方便好看呢?可以采用结构体。
(最新更新单点更新+区间查询模板)
#include P1438 无聊的数列
看到等差数列,自然而然想到差分。
通过举例子看看规律吧!
原 数 组 : 1 2 3 4 5 原数组:1 \ 2\ 3\ 4\ 5 原数组:1 2 3 4 5
要在下标[2,4](l=2,r=4)上加上等差数列 a n = 2 n + 1 a_n=2n+1 an=2n+1(k=2,d=1)(n应从0开始)
新 数 组 : 1 3 6 9 5 新数组:1 \ 3\ 6\ 9\ 5 新数组:1 3 6 9 5
原 差 分 数 组 : 1 1 1 1 1 原差分数组:1 \ 1\ 1\ 1\ 1 原差分数组:1 1 1 1 1
所以
后 差 分 数 组 : 1 2 3 3 − 4 后差分数组:1 \ 2\ 3\ 3\ -4 后差分数组:1 2 3 3 −4
对比一下就可以看出来 (假设差分数组为a)
则 对 于 l : a [ l ] = a [ l ] + k 对于l\ :a[l]=a[l]+k 对于l :a[l]=a[l]+k
对 于 区 间 ( L , R ] : a [ i ] = a [ i ] + d , i ∈ ( L , R ] 对于区间(L,R]:a[i]=a[i]+d,i∈(L,R] 对于区间(L,R]:a[i]=a[i]+d,i∈(L,R]
对 于 R + 1 : a [ R + 1 ] = a [ R + 1 ] − ( k + ( ( r − l ) ∗ d ) 对于R+1:a[R+1]=a[R+1]-(k+((r-l)*d) 对于R+1:a[R+1]=a[R+1]−(k+((r−l)∗d)
代码孕育而生
#include P1276 校门外的树(增强版)
看代码注释即可,没用线段树,数据可能有点水吧。
#include P1020 导弹拦截
没搞懂大佬线段树的意思。
100分的是 O ( n 2 ) O(n^2) O(n2)的dp
200分的得是 O ( n l o g n ) O(nlogn) O(nlogn)的算法,这里用到伟大的STL:upper_bound lower_bound
大佬的题解
注意的是这两个使用时,对象一定得是有序的数组。
如果数组是降序,那么后面得加上greater。升序就不用加了,默认是升序。
其实就是符合就加进去,不符合就把不合适的换掉。
#include NEFU2200数据区间查询-线段树
单点更新+求最小值
#include NEFU1476维护序列-线段树
和洛谷模板2相同。
#include NEFU1475花神游历各国-线段树
维护一个区间的最大值+单点修改+区间查询。
当一个区间的最大值为1时,就不用开方了。(要不然浪费时间)
#include NEFU1473A Simple Problem with Integers-线段树
同模板1
NEFU1472区间和-线段树
#include NEFU1465校门外的树3-线段树
一开始想的这题是,区间更新+找最大值。但其实是不对的。
如果在(1,3) (4,6)种树,那么查询(2,4)的最大值还是1。
正解是括号序列的思想。
用两个树状数组维护每个节点左右端点个数,端点数即是该点上覆盖的线段。
用r前面的左括号数量 − - −l前面的右括号数量即可。
附上一张潦草的图。
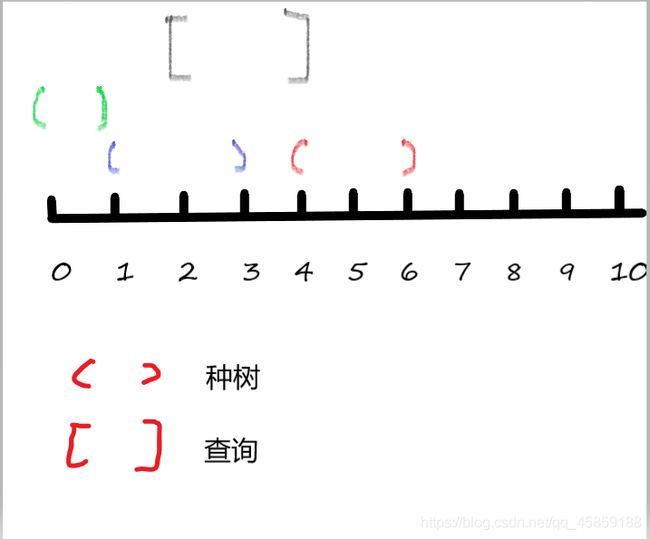
#includeNEFU1266快乐的雨季—线段树
卡了我一手快读,不明白怎么回事。
#include 完结。