量子力学 or 线性代数(一)?
线性代数与量子力学的前世今生(一)
- 一. 猫的叠加态(NOT 非死即生)
- 二. 关于量子力学的一些基本概念。
- 三. 概率,内积,以及本征态的正交性
本博客是博主的在初学量子力学时,感觉自己力不从心,无法将自己所学的知识融会贯通的时候,来自知乎上的一位大神的专栏为我指点迷津,本CSDN专栏文章是对它的理解感悟和自己的一些想法,如果有小伙伴和我一样的受到“不要自学量子力学”的诅咒时,可以去知乎康康他的专栏文章。链接如下:
戳这里~~
一. 猫的叠加态(NOT 非死即生)
首先,我们先从楼下大妈都能说上几句的“薛定谔的猫”开始,为了完整性,先来看看这个实验:
“薛定谔的猫”是由奥地利物理学家薛定谔于1935年提出的有关猫生死叠加的著名思想实验,是把微观领域的量子行为扩展到宏观世界的推演。这里必须要认识量子行为的一个现象:观测。微观物质有不同的存在形式,即粒子和波。通常,微观物质以波的叠加混沌态存在;一旦观测后,它们立刻选择成为粒子。实验是这样的:在一个盒子里有一只猫,以及少量放射性物质。之后,有50%的概率放射性物质将会衰变并释放出毒气杀死这只猫,同时有50%的概率放射性物质不会衰变而猫将活下来 。
根据经典物理学,在盒子里必将发生这两个结果之一,而外部观测者只有打开盒子才能知道里面的结果。在量子的世界里,当盒子处于关闭状态,整个系统则一直保持不确定性的波态,即猫生死叠加。猫到底是死是活必须在盒子打开后,外部观测者观测时,物质以粒子形式表现后才能确定。这项实验旨在论证量子力学对微观粒子世界超乎常理的认识和理解,可这使微观不确定原理变成了宏观不确定原理,客观规律不以人的意志为转移,猫既活又死违背了逻辑思维。
看到这里 ,其实意思我们大多都看懂了,但是还是觉得有点不可思议,好,现在我们不管它,把我们的记忆拉回到大一的时候的一门数学课上:线性代数中向量的线性组合!!
在向量空间中,我们如果定义了一组线性无关的向量基底: { e 1 , e 2 , . . . e n } \left \{e_{1} ,e_{2},... e_{n}\right \} {e1,e2,...en},那么空间中的任意向量可以表示为: α = a 1 e 1 + a 2 e 2 + . . . + a n e n = ∑ i = 1 n a i e i \alpha = a_{1}e_{1} + a_{2}e_{2}+...+ a_{n}e_{n} =\sum_{i = 1}^{n} a_{i}e_{i} α=a1e1+a2e2+...+anen=i=1∑naiei
当然,在这里我们只需要用到二维的就可以了, α = a 1 e 1 + a 2 e 2 \alpha = a_{1}e_{1} + a_{2}e_{2} α=a1e1+a2e2

这个时候,我们再回到那只半死不活的猫。。。。
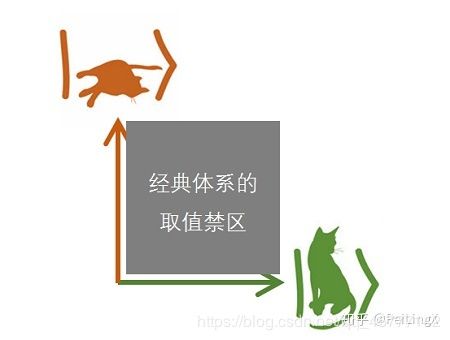
下图中, 两个基底、也就是图中的绿色箭头和红色箭头,分别表示“活猫”和“死猫”两种状态。
 |
 |
|---|---|
| 经典体系下,猫的状态只能落在两个箭头中的一个,而无法出现在两者之间的灰色区域。 | 量子力学,只要我们还没有去观测猫的死活,这只猫可以是两个基底 任意线性叠加形成的抽象的向量。 |
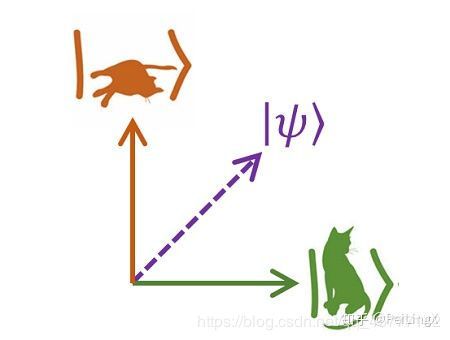
猫的这种“既生又死”的状态,是“生”和“死”两种状态的叠加,可以用一种名叫“狄拉克符号”的奇怪咒语来描述:
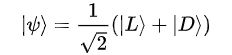
其中 |L> 表示 猫是活的,|D> 表示猫已经死翘翘了~~
形象一点就是这样:

是不是恍然大悟,OMG!! 真是盖了帽了 ,我的老背比。。。。。
不过这个情况 猫死活的概率各占了一半,但是 如果你有像灭霸一样的手套的话,你可以随意改变这个可怜的小猫咪死亡的概率大小(手动滑稽~~),只需要分别把前面的 2 \sqrt{ 2} 2换成 a 1 , a 2 a_{1},a_{2} a1,a2就可以了。
二. 关于量子力学的一些基本概念。
高处不胜寒,既然决定学量子力学,那么注定是孤独且无聊的(手动奸笑~~),枯燥的概念是躲不过去的!!
(1)本征态:
定义一个空间到空间自身的映射(这里不考虑定义域的问 题),如果这个映射的像是原像按照线性空间的数乘乘上一个常数,就称这个常数为这个映射(或者称为算子)的本征值(eigenvalue),这个矢量叫做本征(eigenvector)
简单来说就是:对于某个需要测量的物理量 P 而言,在经典物理中可能被测量到的确定状态,在量子力学中叫做物理量 P 的本征态 (Eigenstate),也就是前面提到的基底。
注意:不同物理量通常对应着不同的本征态,且不同的本征态通常是正交的,和空间单位向量差不多!
所以,“猫的生死”这个“物理量”的本征态就是两个基底 |L> 和 | D>。
(2)态矢量:
量子态由希尔伯特空间中的矢量表征,称为态矢量。该希尔伯特空间又称为态矢量空间或态空间。
补充:希尔伯特空间:也叫态空间,就是由本征态张成的那个抽象空间(这个空间是抽象的,不存在)。
物理含义:以量子力学的角度来看,粒子或者系统总是处于一个概率分布的形式。无论选取哪个物理量来进行观测,总会得到一个几率分布和不可逆地得到一个新量子态。所以说“态”实际上是描述粒子或系统所处的状态;某种意义上来讲就是描述选取各种各样的观测量所带来的几率分布。而把这种概念抽象成一个名词,就是态。
表示 : 我们一般用如下记号来表示一个量子态: ∣ ψ > |\psi> ∣ψ>
态矢量可以有多种表示形式,例如在坐标表象中,态矢量可以用一个函数来表示,如ψ(x),称为波函数或态函数,也即: < x ∣ ψ > = ψ ( x )
在这里 ,我来插一张表格,希望能帮到大家更快的比较量子力学与经典力学:
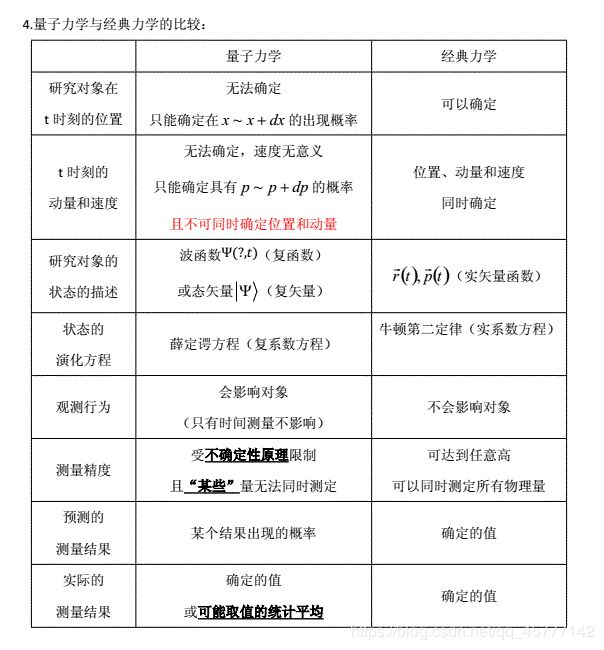
这里有些知识看不懂我觉的也没有关系,日后会再叙的!!
三. 概率,内积,以及本征态的正交性
<1> 概率和内积:
再回到那只可怜的猫咪,毕竟这一切的理论都是在没打开盒子之前的,一旦我们打开盒子去观测它的死活,那么,猫不会再处于叠加态,而是会出现一个确切的结果:要么生、要么死!
这个过程,在量子力学中我们把他叫做 坍缩(collapse),猫的叠加态在观测后,会随机地坍缩到某个确定的征态。

还记得我们刚才说的那个,猫死活的本征态前面的系数 a 1 , a 2 a_{1},a_{2} a1,a2 吗?
其实,这两个系数决定了打开箱子时发现活猫和发现死猫两种结果各自的概率,也就是测量结果坍缩到两个本征态的概率
他们的关系是: a 1 2 + a 2 2 = 1 a_{1}^{2} + a_{2}^{2} =1 a12+a22=1, 且 P ( ∣ L > ) = a 1 2 , P ( ∣ D > ) = a 2 2 P(|L>) = a_{1}^{2}, P(|D>) = a_{2}^{2} P(∣L>)=a12,P(∣D>)=a22
其实,刚开始看到这里,我就蒙B了。。。我垃圾的九年义务教育告诉我,这 tm 不应该是 a 1 + a 2 = 1 a_{1} + a_{2} = 1 a1+a2=1吗?
怎么多出来个平方。
这时候,…(* ̄0 ̄)ノ 噔噔 ~~噔噔,线性代数闪亮抢镜登场。。 大家想一想线代中的啥子知识点 和这个 a 1 2 + a 2 2 = 1 a_{1}^{2} + a_{2}^{2} =1 a12+a22=1是类似的呢??
是不是这个: ( a 1 , a 2 ) ( a 1 a 2 ) = 1 \left (\begin{matrix} a_{1} , a_{2} \\ \end{matrix}\right ) \left (\begin{matrix}a_{1} \\ a_{2} \\\end{matrix}\right )=1 (a1,a2)(a1a2)=1
想起来了吗,这个就是我们当时线代第五章的内积,前面我们说过 一个物理量的叠加态是本征态的线性组合,即: ∣ ψ > = a 1 ∣ L > + a 2 ∣ D > |\psi > =a_{1}|L> +a_{2}|D> ∣ψ>=a1∣L>+a2∣D>
两个本征态可以被视为一组基底,这样,我们就可以将叠加系数自然地写为行向量和列向量的形式。这样,如果用向量的语言来描述,猫生和猫死的总概率就是态矢量 ∣ ψ > |\psi > ∣ψ>与它自身的内积( 记为 < ψ ∣ ψ > <\psi |\psi > <ψ∣ψ>) 。
其实,我们可以将这个类似对称的式子拆成2个
第一个是: < ψ ∣ <\psi | <ψ∣, 称为左矢,又叫 bra , 它对应的是上面我们刚说的行向量: ( a 1 , a 2 ) \left (\begin{matrix} a_{1} , a_{2} \\ \end{matrix}\right ) (a1,a2) 。
第二个是 : ∣ ψ > |\psi > ∣ψ>, 称为右矢, 又叫ket , 它对应的是上面我们刚说的列向量: ( a 1 a 2 ) \left (\begin{matrix}a_{1} \\ a_{2} \\\end{matrix}\right ) (a1a2) 。
注意:
1.左矢和右矢其实描述的都是同一个量子状态,就像行向量和列向量都描述同一个向量一样 。
2. 当我们讨论一个态矢量的时候,通常是用右矢来表示。
3. 我们把左矢(bra)和右矢(ket)放到一起,就代表行向量乘以列向量,也就是向量的内积了,记为 < ψ ∣ ψ > <\psi |\psi > <ψ∣ψ> = 1)
4. 量子力学中叠加态的各个系数,如 a 1 , a 2 a_{1} , a_{2} a1,a2,通常是一个复数而不是实数!
<2> 本征态的正交性
再让我们回到那只可怜的(ΦωΦ),没错,这辈子,我就和那个憨逼猫死磕上了,凸(艹皿艹 )!!!
毫无疑问的是,一旦我们观测的猫之后,叠加态坍缩成本征态,量子力学的一切理论在我们看来也都消失了,因为这个时候,我们能观察到的只能是 死 或者 活 的 ,(你不会以为猫真的有九条命吧,o( ̄︶ ̄)o )。
我们知道,线代中给定一组标准正交基底 { e i e_{i} ei} 后,某向量 α = ∑ i a i e i \alpha = \sum_{i} a_{i}e_{i} α=∑iaiei 的组合系数 a i a_{i} ai可以表示为 α \alpha α 与各基底的内积,即: a i a_{i} ai=< α , e i \alpha,e_{i} α,ei> , 而不同基底之间的正交性,意味着任意两个不同基底的内积就是 0 。
再回首:我们把态矢量的内积做一个扩展,定义两个不同态矢量 ∣ ψ > , ∣ ϕ > |\psi >, |\phi > ∣ψ>,∣ϕ>,假设他们在一组线性无关的基底下表示为
∣ ϕ > = [ b 1 b 2 ⋮ b n ] , ∣ ψ > = [ a 1 a 2 ⋮ a n ] |\phi> =\begin{bmatrix}{b_{1}}\\{b_{2}}\\{\vdots}\\{b_{n}}\\\end{bmatrix} , |\psi> = \begin{bmatrix}{a_{1}}\\{a_{2}}\\{\vdots}\\{a_{n}}\\\end{bmatrix} ∣ϕ>=⎣⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎤,∣ψ>=⎣⎢⎢⎢⎡a1a2⋮an⎦⎥⎥⎥⎤
根据内积规则,转置一下则有: < ϕ ∣ ψ > = [ b 1 b 2 ⋯ b n ] [ a 1 a 2 ⋮ a n ] = ∑ k a k b k <\phi|\psi > = \begin{bmatrix} {b_{1}}&{b_{2}}&{\cdots}&{b_{n}}\\ \end{bmatrix} \begin{bmatrix}{a_{1}}\\{a_{2}}\\{\vdots}\\{a_{n}}\\\end{bmatrix} = \sum_{k} a_{k}b_{k} <ϕ∣ψ>=[b1b2⋯bn]⎣⎢⎢⎢⎡a1a2⋮an⎦⎥⎥⎥⎤=k∑akbk
现在,我们假设, | ϕ \phi ϕ> 正好是一个基底,记为 ∣ e i > |e_{i}> ∣ei> ,则 ∣ ψ > |\psi> ∣ψ> 在这个基底的组合系数为:
a i = < e i ∣ ψ > a_{i} =
目前为止,这些性质本质上都和我们在线性代数中看到的一样,只是换了一套符号而已。如果这些性质都遗忘了,赶紧打开那尘封已久的 由同济出版的葵花宝典到 P 114 页,沙雕~~。
自此,本部分内容到这就告一段落,欲知详情,静待下回讲解,当然了,笔者是会坚持更新的,既然都看到这里了,就别忘了用你那发财的小手指 点一下关注吧,博主也只是在校计科 单身狗一个,希望小伙伴们多多支持啊!!

