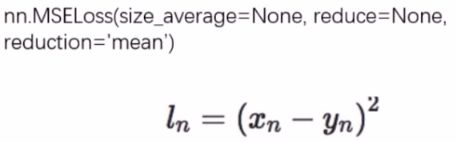系统学习Pytorch笔记六:模型的权值初始化与损失函数介绍
Pytorch官方英文文档:https://pytorch.org/docs/stable/torch.html?
Pytorch中文文档:https://pytorch-cn.readthedocs.io/zh/latest/
1. 写在前面
疫情在家的这段时间,想系统的学习一遍Pytorch基础知识,因为我发现虽然直接Pytorch实战上手比较快,但是关于一些内部的原理知识其实并不是太懂,这样学习起来感觉很不踏实, 对Pytorch的使用依然是模模糊糊, 跟着人家的代码用Pytorch玩神经网络还行,也能读懂,但自己亲手做的时候,直接无从下手,啥也想不起来, 我觉得我这种情况就不是对于某个程序练得不熟了,而是对Pytorch本身在自己的脑海根本没有形成一个概念框架,不知道它内部运行原理和逻辑,所以自己写的时候没法形成一个代码逻辑,就无从下手。 这种情况即使背过人家这个程序,那也只是某个程序而已,不能说会Pytorch, 并且这种背程序的思想本身就很可怕, 所以我还是习惯学习知识先有框架(至少先知道有啥东西)然后再通过实战(各个东西具体咋用)来填充这个框架。 而这个系列的目的就是在脑海中先建一个Pytorch的基本框架出来, 学习知识,知其然,知其所以然才更有意思 。
今天是该系列的第六篇文章, 在上一次nn的网络层介绍(卷积层,池化层,激活函数,全连接层等)的基础上继续学习,我们通过上一次的学习,基本上完成了模型模块,也学会了如何搭建网络模型,下面进入损失函数的模块,但是在这之前,先来看看常用的权值初始化方法,这是网络模型搭建好之后的一个非常重要的步骤,正确的权值初始化可以加速模型的收敛, 不恰当的权值初始化导致输出层的输出过大或者过小,最终导致梯度爆炸或者消失,使得模型无法训练, 这里会深层剖析权重初始化的重要性,会学习适用于饱和激活函数tanh等的Xavier初始化方法和非饱和激活函数relu等的Kaiming初始化方法(这些在实践中非常常用,但是有时候并不知道用这个背后的原因),学习完了这个,然后再正式整理关于各种损失函数的一些知识,这里会学习18种损失函数的原理及使用,最后会对这18种损失函数梳理一下,得知道什么样的任务有哪些损失函数可用。通过这篇文章,可以打通权值初始化和损失函数的任督二脉。
注意,本系列都默认已经安装了Cuda,搭建好了Pytorch环境,如果你电脑是Windows,并且没有装Pytorch,那么巧了, 我之前写过一篇怎么搭建环境,可以先看看 Pytorch入门+实战系列一:Windows下的Pytorch环境手把手搭建
大纲如下:
- 权值初始化(梯度消失与爆炸, Xavier方法与Kaiming方法, 十种初识化方法)
- 损失函数(损失函数,代价函数,目标函数这哥仨不是一回事,交叉熵损失, NLL/BCE/BCEWithLogits Loss)
- 总结梳理
Ok, let’s go!
2. 权值初始化
在网络模型搭建完成之后,对网络中的权重进行合适的初始化是非常重要的一个步骤, 初始化好了,比如正好初始化到模型的最优解附近,那么模型训练起来速度也会非常的快, 但如果初始化不好,离最优解很远,那么模型就需要更多次迭代,有时候还会引发梯度消失和爆炸现象, 所以正确的权值初始化还是非常重要的,下面我们就来看看常用的权值初始化的方法,但是在这之前,先了解一下什么是梯度消失和梯度爆炸现象。
2.1 梯度的消失和爆炸
我们以上一篇的一个图来看一下梯度消失和爆炸现象
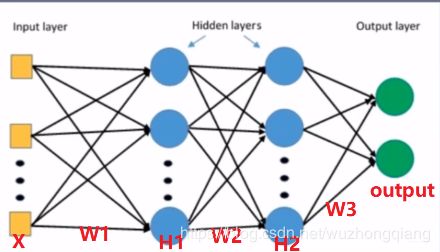
看上面这个图, 假设我们要算 W 2 W_2 W2的梯度,我们根据链式法则应该是下面这样:
H 2 = H 1 ∗ W 2 \mathrm{H}_{2}=\mathrm{H}_{1} * \mathrm{W}_{2} H2=H1∗W2
Δ W 2 = ∂ L o s s ∂ W 2 = ∂ L o s s ∂ o u t ∗ ∂ o u t ∂ H 2 ∗ ∂ H 2 ∂ w 2 = ∂ L o s s ∂ o u t ∗ ∂ o u t ∂ H 2 ∗ H 1 \begin{aligned} \Delta W_{2} &=\frac{\partial L o s s}{\partial W_{2}}=\frac{\partial L o s s}{\partial o u t} * \frac{\partial o u t}{\partial H_{2}} * \frac{\partial H_{2}}{\partial w_{2}} \\ &=\frac{\partial L o s s}{\partial o u t} * \frac{\partial o u t}{\partial H_{2}} * H_{1} \end{aligned} ΔW2=∂W2∂Loss=∂out∂Loss∗∂H2∂out∗∂w2∂H2=∂out∂Loss∗∂H2∂out∗H1
这样我们就会发现 W 2 W_2 W2梯度的求解过程中会用到上一层神经元的输出值 H 1 H_1 H1, 那么这时候,如果 H 1 H_1 H1的输出值非常小,那么 W 2 W_2 W2的梯度也会非常小,这时候就有可能造成梯度消失的现象,尤其是当网络层很多的时候,这种连乘一个数非常小,就会导致越乘越小,后面的层里面就容易发现梯度消失。 而当 H 1 H_1 H1非常大的时候,当然也就会发生梯度爆炸。
H 1 → 0 ⇒ Δ W 2 → 0 H 1 → ∞ ⇒ Δ W 2 → ∞ \begin{aligned} &\mathrm{H}_{1} \rightarrow \mathbf{0} \Rightarrow \Delta \mathrm{W}_{2} \rightarrow \mathbf{0}\\ &\mathrm{H}_{1} \rightarrow \infty \Rightarrow \Delta \mathrm{W}_{2} \rightarrow \infty \end{aligned} H1→0⇒ΔW2→0H1→∞⇒ΔW2→∞
一旦发生梯度消失或者爆炸, 就会导致模型无法训练,而如果想避免这个现象,我们就得控制网络输出层的一个尺度范围,也就是不能让它太大或者太小。那么我们怎么控制这个网络输出层的尺度呢? 那就是通过合理的初始化权重了。我们下面从代码切入,进行理解吧:
我们建立一个100层的多层感知机,每一层256个神经元,我们使用上面学习的ModuleList进行建立:
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.neural_num = neural_num
# 正向传播
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
print("layer:{}, std:{}".format(i, x.std()))
if torch.isnan(x.std()):
print('output is nan in {} layers".format(i))
break
return x
# 权值初始化,我们这里使用标准正态
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.normal_(m.weight.data) # normal: mean=0, std=1
# 用一下网络
layer_nums = 100
neural_nums = 256
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
print(output)
这个结果可以发现,在35层的时候,神经网络的输出就成了nan, 这说明网络出现了问题,导致后面输出的值太大了, 当然我们还没有反向传播, 根据上面的权重推导的公式,后面的这些如果为nan了之后,反向传播的时候,这些权重根本就没法进行更新,会发生梯度爆炸现象。
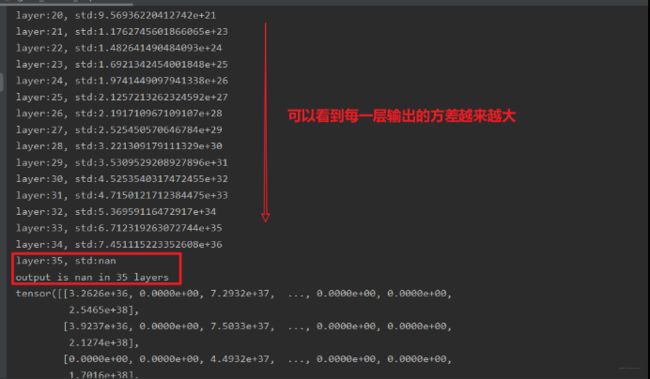
这就是有时候我们在训练网络的时候,最后结果全是nan的原因,这往往可能是权重初始化的不当导致的。
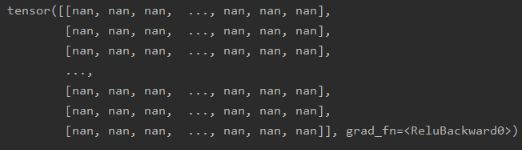
可是,这是为啥呢? 为啥我初始化权重不当了会影响到网络的输出呢? 刚才不是还说是网络的输出影响的权重梯度吗? 那是反向传播的时候, 而正向传播的时候,权重肯定要影响到每一层的输出啊。 我们推导一下上面这个过程中每一层输出的方差是如何变化的就明白了。
下面先进行一个 D ( X Y ) D(XY) D(XY)方差的公式推导:
借助三个基本公式:
- E ( X Y ) = E ( X ) E ( Y ) E(XY) = E(X)E(Y) E(XY)=E(X)E(Y)
- D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 D(X) = E(X^2) - [E(X)]^2 D(X)=E(X2)−[E(X)]2
- D ( X + Y ) = D ( X ) + D ( Y ) D(X+Y) = D(X) + D(Y) D(X+Y)=D(X)+D(Y)
那么
D ( X Y ) = E [ X Y − E ( X Y ) ] 2 = E X ² Y ² − 2 X Y E ( X Y ) + E ² ( X Y ) = E ( X ² ) E ( Y ² ) − 2 E ² ( X ) E ² ( Y ) + E ² ( X ) E ² ( Y ) = E ( X ² ) E ( Y ² ) − E ² ( X ) E ² ( Y ) = ( D ( X ) + [ E ( X ) ] 2 ) ( D ( Y ) + [ E ( Y ) ] 2 ) − E ( X ² ) E ( Y ² ) − E ² ( X ) E ² ( Y ) = D ( X ) D ( Y ) + D ( X ) [ E ( Y ) ] 2 + D ( Y ) [ E ( X ) ] 2 D(XY)\\=E{[XY-E(XY)]^2}\\=E{X²Y²-2XYE(XY)+E²(XY)}\\=E(X²)E(Y²)-2E²(X)E²(Y)+E²(X)E²(Y)\\=E(X²)E(Y²)-E²(X)E²(Y)\\=(D(X)+[E(X)]^2)(D(Y)+[E(Y)]^2)-E(X²)E(Y²)-E²(X)E²(Y)\\=D(X)D(Y) + D(X)[E(Y)]^2+D(Y)[E(X)]^2 D(XY)=E[XY−E(XY)]2=EX²Y²−2XYE(XY)+E²(XY)=E(X²)E(Y²)−2E²(X)E²(Y)+E²(X)E²(Y)=E(X²)E(Y²)−E²(X)E²(Y)=(D(X)+[E(X)]2)(D(Y)+[E(Y)]2)−E(X²)E(Y²)−E²(X)E²(Y)=D(X)D(Y)+D(X)[E(Y)]2+D(Y)[E(X)]2
若 E ( X ) = 0 , E ( Y ) = 0 E(X)=0, E(Y)=0 E(X)=0,E(Y)=0, 则 D ( X Y ) = D ( X ) D ( Y ) D(XY) = D(X)D(Y) D(XY)=D(X)D(Y)
好了, 那么我们看看神经网络里面每一层输出的方差计算:
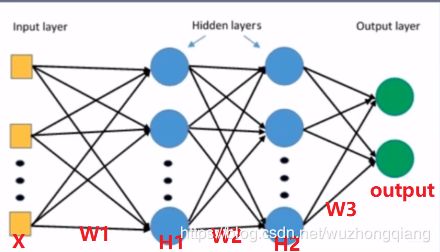
还是这个网络,我们看第一层第一个神经元的方差应该怎么算:
H 11 = ∑ i = 0 n X i ∗ W 1 i D ( H 11 ) = ∑ i = 0 n D ( X i ) ∗ D ( W 1 i ) = n ∗ ( 1 ∗ 1 ) = n std ( H 11 ) = D ( H 11 ) = n \begin{aligned} \mathrm{H}_{11}=& \sum_{i=0}^{n} X_{i} * W_{1 i} \quad \\ \mathrm{D}\left(\mathrm{H}_{11}\right) &=\sum_{i=0}^{n} D\left(X_{i}\right) * D\left(W_{1 i}\right) \\ &=\mathrm{n} *(1 * 1) \\ &=\mathrm{n} \\ \operatorname{std}\left(\mathrm{H}_{11}\right) &=\sqrt{\mathrm{D}\left(\mathrm{H}_{11}\right)}=\sqrt{n} \end{aligned} H11=D(H11)std(H11)i=0∑nXi∗W1i=i=0∑nD(Xi)∗D(W1i)=n∗(1∗1)=n=D(H11)=n
这里我们的输入数据和权重都初始化的均值为0,方差为1的标准正态。 这样经过一个网络层就发现方差扩大了n倍。 而我们上面用了100个网络层, 那么这个方差会指数增长,所以我们后面才会出现输出层方差nan的情况。
那么我们怎么解决这种情况呢? 那很简单,让网络层的输出方差保持尺度不变就可以了, 可是怎么做呢? 分析一下网络层的输出方差:

我们发现,每一层的输出方差会和每一层神经元个数,前一层输出方差和本层权重的方差有关,如果想让方差的尺度不变,因为这里都是连乘,有个方法就是让每一层输出方差都是1, 也就是 D ( H 11 ) = 1 D(H_{11})=1 D(H11)=1, 这样后面多层相乘,那么也不会变这个尺度。 怎么做呢? 首先, 每一层神经元个数没法变, 而前一层输出方差是1又涉及到了方差, 所以这里能变得就是权重的方差:
D ( H 1 ) = n × D ( X ) × D ( W ) = 1 D ( W ) = 1 n = > s t d ( W ) = 1 n D(H_1) = n\times D(X) \times D(W) = 1\\D(W) = \frac{1}{n} => std(W) = \sqrt{\frac{1}{n}} D(H1)=n×D(X)×D(W)=1D(W)=n1=>std(W)=n1
这样,我们权重在初识的时候,方差如果是 1 n \sqrt{\frac{1}{n}} n1的话,每一层的输入方差都是1, 这样方差就不会导致nan的情况发生了。在上面代码中改一句话:
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num)) # 把权重方差改了
这样就会发现,不会出现nan的情况了:

所以我们只要采用恰当的权值初始化方法,就可以实现多层神经网络的输出值的尺度维持在一定范围内, 这样在反向传播的时候,就有利于缓解梯度消失或者爆炸现象的发生
当然,上面的网络只是一个线性网络,在实际中我们还得考虑激活函数的存在,我们从上面的前向传播中加一个激活函数再看一下结果:
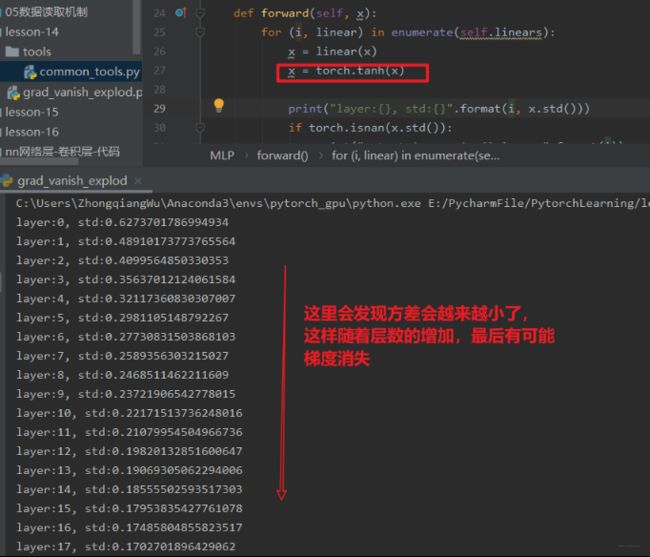
那么,具有激活函数的时候,怎么对权重进行初始化呢?
2.2 Xavier初始化
方差一致性:保持数据尺度范围维持在恰当范围, 通常方差为1。 如果有了激活函数之后,我们应该怎么对权重初始化呢?
2010年Xavier发表了一篇文章,详细探讨了如果有激活函数的时候,如何进行权重初始化, 当然它也是运用的方差一致性原则, 但是它这里考虑的是饱和激活函数, 如sigmoid, tanh。 文章中有个这样的公式推导,从而得到我们权重的方差:
n i ∗ D ( W ) = 1 n i + 1 ∗ D ( W ) = 1 ⇒ D ( W ) = 2 n i + n i + 1 \begin{aligned} &\boldsymbol{n}_{i} * {D}({W})={1}\\ &\boldsymbol{n}_{i+1} * {D}({W})={1}\\ &\Rightarrow D(W)=\frac{2}{n_{i}+n_{i+1}} \end{aligned} ni∗D(W)=1ni+1∗D(W)=1⇒D(W)=ni+ni+12
这里的 n i n_i ni、 n i + 1 n_{i+1} ni+1分别指的输入层和输出层神经元个数。通常Xavier采用均匀分布对权重进行初始化,那么我们可以推导一下均匀分布的上限和下限:
W ∼ U [ − a , a ] D ( W ) = ( − a − a ) 2 12 = ( 2 a ) 2 12 = a 2 3 \begin{aligned} &{W} \sim \boldsymbol{U}[-{a}, {a}]\\ &D(W)=\frac{(-a-a)^{2}}{12}=\frac{(2 a)^{2}}{12}=\frac{a^{2}}{3} \end{aligned} W∼U[−a,a]D(W)=12(−a−a)2=12(2a)2=3a2
我们让上面的两个 D ( W ) D(W) D(W)相等就会得到
2 n i + n i + 1 = a 2 3 ⇒ a = 6 n i + n i + 1 ⇒ W ∼ U [ − 6 n i + n i + 1 , 6 n i + n i + 1 ] \begin{array}{l} \frac{2}{n_{i}+n_{i+1}}=\frac{a^{2}}{3} \Rightarrow a=\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}} \\ \Rightarrow W \sim U\left[-\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}, \frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}\right] \end{array} ni+ni+12=3a2⇒a=ni+ni+16⇒W∼U[−ni+ni+16,ni+ni+16]
这就是Xavier初始化方法, 那么在代码中怎么用呢? 还是上面的那个代码例子,我们在参数初始化里面用Xavier初始化权重:
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
# Xavier初始化权重
tanh_gain = nn.init.calculate_gain('tanh')
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)
这里面用到了一个函数nn.init.calculate_gain(nonlinearity, param=None)这个函数的作用是计算激活函数的方差变化尺度, 怎么理解这个方差变化尺度呢?其实就是输入数据的方差除以经过激活函数之后的输出数据的方差。nonlinearity表示激活函数的名称,如tanh, param表示激活函数的参数,如Leaky ReLU的negative_slop。 (这里不用也行,但得知道这个方法)。这时候再来看一下最后的结果:
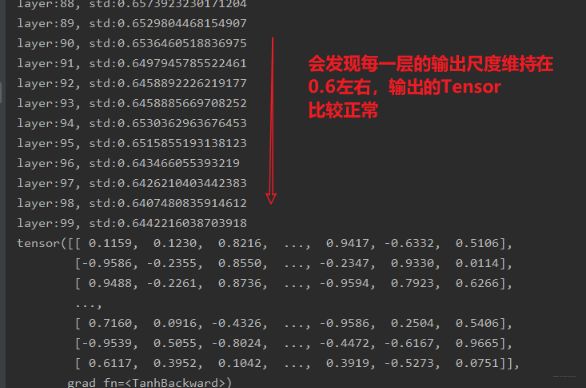
所以Xavier权重初始化,有利于缓解带有sigmoid,tanh的这样的饱和激活函数的神经网络的梯度消失和爆炸现象。
但是,2012年AlexNet出现之后,非饱和函数relu也用到了神经网络中,而Xavier初始化对于relu就不好使了,不信我们看看:

2.3 Kaiming初始化
这个依然是考虑的方差一致性原则,**针对的激活函数是ReLU及其变种。**经过公示推导,最后的权值标准差是这样的:
D ( W ) = 2 n i D ( W ) = 2 ( 1 + a 2 ) + n i std ( W ) = 2 ( 1 + a 2 ) ∗ n i \begin{aligned} &\mathbf{D}({W})=\frac{2}{\boldsymbol{n}_{i}}\\ &\mathbf{D}({W})=\frac{2}{\left(1+\mathbf{a}^{2}\right)+\boldsymbol{n}_{i}}\\ &\operatorname{std}(W)=\sqrt{\frac{2}{\left(1+a^{2}\right) * n_{i}}} \end{aligned} D(W)=ni2D(W)=(1+a2)+ni2std(W)=(1+a2)∗ni2
那么Kaiming初始化权重方法怎么用呢?
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.kaiming_normal_(m.weight.data)
# nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num)) # 这两句话其实作用一样,不过自己写还得计算出标准差
我们可以看一下结果:
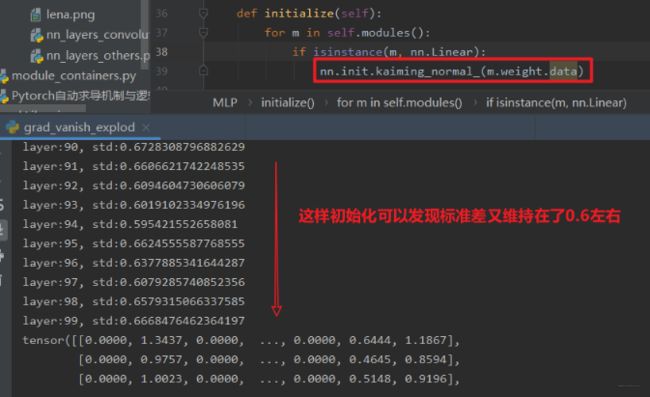
所以从上面的学习中,我们对权值的初始化有了清晰的认识,发现了权重初始化对于模型的重要性,不好的权重初始化方法会引起输出层的输出值过大过小,从而引发梯度的消失或者爆炸,最终导致我们的模型无法训练。所以我们如果想缓解这种现象,就得控制输出层的值的范围尺度,就得采取合理的权重初始化方法。
2.4 十种权重初始化方法
Pytorch里面提供了很多权重初始化的方法,可以分为下面的四大类:
- 针对饱和激活函数(sigmoid, tanh):Xavier均匀分布, Xavier正态分布
- 针对非饱和激活函数(relu及变种):Kaiming均匀分布, Kaiming正态分布
- 三个常用的分布初始化方法:均匀分布,正态分布,常数分布
- 三个特殊的矩阵初始化方法:正交矩阵初始化,单位矩阵初始化,稀疏矩阵初始化:
好了,到了这里,模型模块才算得上结束, 下面我们就进行下一个模块的学习,损失函数模块,在这里面学习各种损失函数的原理及应用场景。
3. 损失函数
这一部分分为三大块, 首先看一下损失函数到底是干嘛的? 然后学习非常常用的损失函数交叉熵,最后再看看其他的几个重要损失函数。
3.1 损失函数初步介绍
损失函数: 衡量模型输出与真实标签的差异。而我们谈损失函数的时候,往往会有三个概念: 损失函数, 代价函数, 目标函数。 你知道这仨到底啥区别吗? 还是以为这仨就是一个概念?
- Loss Function: 计算一个样本的一个差异。 L o s s = f ( y ∧ , y ) Loss = f(y^{\wedge},y) Loss=f(y∧,y)
- Cost Function: 计算整个训练集Loss的一个平均值。 cos t = 1 N ∑ i N f ( y i ∧ , y i ) \cos t=\frac{1}{N} \sum_{i}^{N} f\left(y_{i}^{\wedge}, y_{i}\right) cost=N1∑iNf(yi∧,yi)
- Objective Function: 这是一个更广泛的概念,在机器学习模型训练中,这是最终的一个目标,过拟合和欠拟合之间进行一个权衡。 O b j = C o s t + R e g u l a r i z a t i o n Obj = Cost + Regularization Obj=Cost+Regularization
而我们一般都是在衡量模型输出和真实标签的差异的时候,往往都直接成损失函数。 但是我们得知道这哥仨不是一回事。我们下面看一下Pytorch中的损失函数的真实面目:

我们发现了啥? 原来_Loss也是继承于Module,这个在模型创建的时候就已经很熟悉了,也具体介绍过, 既然_Loss也是继承于这个类,那么就得先想起来肯定_Loss也有那8个参数字典了,然后这里面是设置一个reduction这个参数。 下面我们再以人民币二分类的实验中的交叉熵损失为例子,看看损失函数是如何创建和使用的,背后的运行机制又是什么?哈哈哈, 下面就得来一波调试了。 这次是损失函数的学习,所以我们在定义损失函数和使用损失函数的地方打上断点,并且开始debug:

程序运行到第一个断点处,我们步入,就到了loss.py文件中的一个class CrossEntropyLoss(_WeightedLoss):交叉熵损失类的__init__方法, 这里发现交叉熵损失函数继承_WeightedLoss这个类:
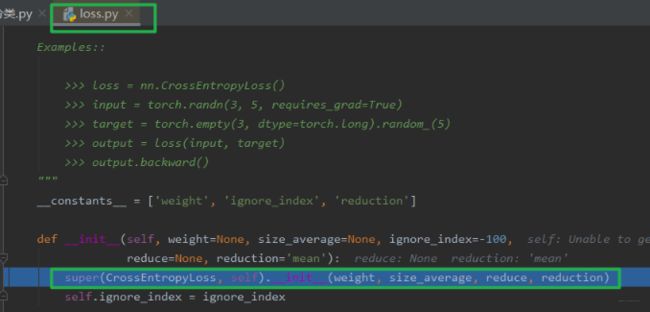
我们继续步入,就到了class _WeightedLoss(_Loss):这个类里面,就会发现这个类继承_Loss, 那么我们继续步入,就到了_Loss这个类里面去,会发现这个继承Module,那么现在就明白了,损失函数的初始化方法和模型其实类似,也是调用Module的初始化方法,最终会有8个属性字典, 然后就是设置了一个reduction这个参数。 初始化就是这样子了, 学过了nn.Module之后,这里都比较好理解。
那么下面看看使用过程中的运行机制:我们到第二个断点,然后步入,我们知道既然这个损失函数也是一个Module,那么在调用的时候肯定也是调用的forward方法了, 还真的是这样, 它也有一个forward的函数的:
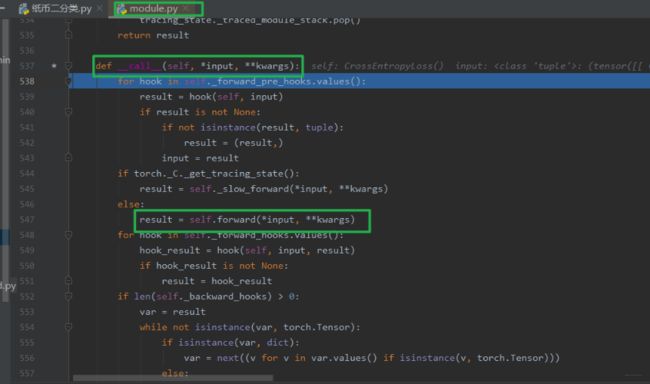
看这里也是调用的forward函数,我们把程序运行到547行,再次步入,看看损失函数的forward长啥样:
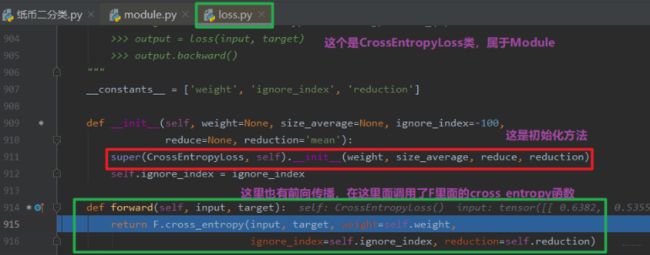
我们模型构建里面forward里面写的是各个模块的拼接方式,而损失函数的forward里面调用了F里面的各种函数,我们Ctrl然后点击这个函数,看看这个交叉熵损失函数到底长啥样:

这个是底层计算了,不再往下了,我们退回去。
这就是损失函数的初始化和使用方法的内部运行机制了。从上面我们发现了损失函数其实也是一个Module, 那么既然是Module,初始化依然是有8个属性字典,使用的方法依然是定义在了forward函数中。 下面我们就详细的学习一个非常重要的函数,也是上面例子里面的函数nn.CrossEntropyLoss, 这个在分类任务中很常用, 所以下面得详细的说说。
3.2 交叉熵损失CrossEntropyLoss
nn.CrossEntropyLoss: nn.LogSortmax()与nn.NLLLoss()结合,进行交叉熵计算。

- weight:各类别的loss设置权值
- ignore_index: 忽略某个类别
- reduction: 计算模式,可为none/sum/mean, none表示逐个元素计算,这样有多少个样本就会返回多少个loss。 sum表示所有元素的loss求和,返回标量, mean所有元素的loss求加权平均(加权平均的含义下面会提到),返回标量。看了下面的原理就懂了。
在详细介绍这些参数用法之前,得先说说这里的交叉熵损失函数,这个并不是公式意义上的交叉熵损失函数,而是有一些不同之处。还记得普通的交叉熵损失函数吗?
H ( P , Q ) = − ∑ i = 1 N P ( x i ) log Q ( x i ) \mathrm{H}(\boldsymbol{P}, \boldsymbol{Q})=-\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) \log \boldsymbol{Q}\left(\boldsymbol{x}_{i}\right) H(P,Q)=−i=1∑NP(xi)logQ(xi)
P P P表示数据的原始分布, Q Q Q表示模型输出的分布,交叉熵损失衡量两个分布之间的差异程度,交叉熵越低,说明两个分布越近。这里的一个不同就是先用nn.LogSoftmax()把模型的输出值归一化成了概率分布的形式,然后是单个样本的输出,并且没有求和符号。
具体的下面会解释,但是解释之前,得先明白一个问题,就是为什么交叉熵可以衡量两个分布的差异,这个到底是个什么东西? 这就不得不提到相对熵, 而想了解相对熵,就得先明白熵的概念,而如果想明白熵,就得先知道自信息,好吧,成功懵逼。 下面我们先看看这些都是啥吧:
首先从熵开始,这是信息论之父香农从热力学借鉴来的名词,用来描述事件的不确定性,一个事物不确定性越大,熵就越大。 比如明天会下雨这个熵就比明天太阳从东边升起这个熵要大。 那么熵的公式长这样:
H ( P ) = E x ∼ p [ I ( x ) ] = − ∑ i N P ( x i ) l o g P ( x i ) \mathrm{H}(\mathrm{P})=E_{x \sim p}[\boldsymbol{I}(\boldsymbol{x})]=-\sum_{i}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) \boldsymbol{l o g} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) H(P)=Ex∼p[I(x)]=−i∑NP(xi)logP(xi)
原来这个熵是自信息的一个期望, 那么就得先看看自信息是什么东西?下面是自信息的公式:
I ( x ) = − log [ p ( x ) ] I(x)=-\log [p(x)] I(x)=−log[p(x)]
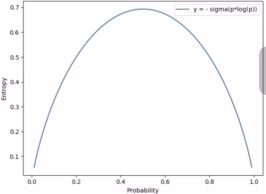
这个比较好理解了,就是一个事件发生的概率,然后取对数再取反。 也就是一个事件如果发生的概率越大,那么自信息就会少。所有事件发生的概率都很大,那么熵就会小,则事件的不确定性就小。 看个图就好理解了:
这是一个两点分布的一个信息熵,可以看到,当概率是0.5的时候熵最大,也就是事件的不确定性最大,熵大约是0.69。 这个数是不是很熟悉?因为这个在二分类模型中经常会碰到,模型训练坏了的时候,或者刚训练的时候,我们就会发现Loss值也可能是0.69,这时候就说模型目前没有任何的判断能力。 这就是信息熵的概念。
相对熵又称为KL散度,用来衡量两个分布之间的差异,也就是两个分布之间的距离,但是不是一个距离函数,因为距离函数有对称性,也就是p到q的距离等于q到p的距离。而这里的相对熵不具备这样的对称性, 如果看过我写的生成对抗原理推导那篇博客的话,那里面也有KL散度这个概念,并且可以通过组合这个得到一个既能够衡量分布差异也有对称性的一个概念叫做JS散度。这里先不说了,看看这个公式:
D K L ( P , Q ) = E x ∼ p [ log P ( x ) Q ( x ) ] \boldsymbol{D}_{K L}(\boldsymbol{P}, \boldsymbol{Q})=\boldsymbol{E}_{\boldsymbol{x} \sim \boldsymbol{p}}\left[\boldsymbol{\operatorname { l o g }} \frac{\boldsymbol{P}(\boldsymbol{x})}{\boldsymbol{Q}(\boldsymbol{x})}\right] DKL(P,Q)=Ex∼p[logQ(x)P(x)]
这里的P是数据的真实分布,Q是模型输出的分布,这里就是用Q的分布去逼近P的分布。所以这不具备对称性。
好了信息熵和相对熵都说了,就可以引出交叉熵了。其实交叉熵=信息熵+相对熵, 公式如下:
H ( P , Q ) = − ∑ i = 1 N P ( x i ) log Q ( x i ) \mathrm{H}(\boldsymbol{P}, \boldsymbol{Q})=-\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) \log \boldsymbol{Q}\left(\boldsymbol{x}_{i}\right) H(P,Q)=−i=1∑NP(xi)logQ(xi)
什么? 没看出交叉熵等于上面两个熵之和吗? 那么我们把相对熵化简一下子:
D K L ( P , Q ) = E x ∼ p [ log P ( x ) Q ( x ) ] = E x ∼ p [ log P ( x ) − log Q ( x ) ] = ∑ i = 1 N P ( x i ) [ log P ( x i ) − log Q ( x i ) ] = ∑ i = 1 N P ( x i ) log P ( x i ) − ∑ i = 1 N P ( x i ) log Q ( x i ) = − 信 息 熵 + 交 叉 熵 \begin{aligned} \boldsymbol{D}_{K L}(\boldsymbol{P}, \boldsymbol{Q}) &=\boldsymbol{E}_{x \sim p}\left[\log \frac{\boldsymbol{P}(\boldsymbol{x})}{Q(\boldsymbol{x})}\right] \\ &=\boldsymbol{E}_{\boldsymbol{x} \sim \boldsymbol{p}}[\log \boldsymbol{P}(\boldsymbol{x})-\log \boldsymbol{Q}(\boldsymbol{x})] \\ &=\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right)\left[\log \boldsymbol{P}\left(\boldsymbol{x}_{i}\right)-\log \boldsymbol{Q}\left(\boldsymbol{x}_{i}\right)\right] \\ &=\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) \log \boldsymbol{P}\left(\boldsymbol{x}_{i}\right)-\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) \log \boldsymbol{Q}\left(\boldsymbol{x}_{i}\right) \end{aligned}\\ =-信息熵 + 交叉熵 DKL(P,Q)=Ex∼p[logQ(x)P(x)]=Ex∼p[logP(x)−logQ(x)]=i=1∑NP(xi)[logP(xi)−logQ(xi)]=i=1∑NP(xi)logP(xi)−i=1∑NP(xi)logQ(xi)=−信息熵+交叉熵
这样看出来了吧。
所以,根据上面的推导我们得到:
H ( P , Q ) = D K L ( P , Q ) + H ( P ) \mathrm{H}(\boldsymbol{P}, \boldsymbol{Q})=\boldsymbol{D}_{K L}(\boldsymbol{P}, \boldsymbol{Q})+\mathrm{H}(\boldsymbol{P}) H(P,Q)=DKL(P,Q)+H(P)
在机器学习模型中,我们最小化交叉熵,其实就是最小化相对熵,因为我们训练集取出来之后就是固定的了,熵就是一个常数。
好了,我们已经知道了交叉熵是衡量两个分布之间的距离,一个差异。所以这里使用softmax,就可以将一个输出值转换到概率取值的一个范围。我们看看这里的交叉熵损失函数是怎么计算的:
loss ( x , class ) = − log ( exp ( x [ class ] ) ∑ j exp ( x [ j ] ) ) = − x [ class ] + log ( ∑ j exp ( x [ j ] ) ) \begin{aligned} &\operatorname{loss}(x, \text { class })=-\log \left(\frac{\exp (x[\text { class }])}{\sum_{j} \exp (x[j])}\right)=-x[\text { class }]+\log \left(\sum_{j} \exp (x[j])\right)\end{aligned} loss(x, class )=−log(∑jexp(x[j])exp(x[ class ]))=−x[ class ]+log(j∑exp(x[j]))
这里的x就是我们输出的概率值,class就是某一个类别,在括号里面执行了一个softmax,把某个神经元的输出归一化成了概率取值,然后-log一下,就得到了交叉熵损失函数。我们可以对比一下我们的交叉熵公式:
H ( P , Q ) = − ∑ i = 1 N P ( x i ) log Q ( x i ) \mathrm{H}(\boldsymbol{P}, \boldsymbol{Q})=-\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) \log \boldsymbol{Q}\left(\boldsymbol{x}_{i}\right) H(P,Q)=−i=1∑NP(xi)logQ(xi)
由于是某个样本,那么 P ( x i ) P(x_i) P(xi)已经是1了,毕竟取出来了已经。 而是某个样本,所以也不用求和符号。
这就是用softmax的原因了,把模型的输出值转成概率分布的形式,这样就得到了交叉熵损失函数。
好了,这里就可以说一说那些参数的作用了, 第一个参数weight, 各类别的loss设置权值, 如果类别不均衡的时候这个参数很有必要了,加了之后损失函数变成这样:
loss ( x , class ) = weight [ class ] ( − x [ class ] + log ( ∑ j exp ( x [ j ] ) ) ) \begin{aligned}&\operatorname{loss}(x, \text { class })=\text { weight }[\text { class }]\left(-x[\text { class }]+\log \left(\sum_{j} \exp (x[j])\right)\right) \end{aligned} loss(x, class )= weight [ class ](−x[ class ]+log(j∑exp(x[j])))
这样,就是如果我们想让模型更关注某一类的话,就可以把这一类的权值设置的大一点。第二个参数ignore_index, 这个是表示某个类别不去计算loss。而关于第三个参数reduction, 有三个计算模式none/sum/mean, 上面已经说了,下面我们从代码中看看这三个的区别:
# fake data
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float) # 这里就是模型预测的输出, 这里是两个类,可以看到模型输出是数值,我们得softmax一下转成分布
target = torch.tensor([0, 1, 1], dtype=torch.long) # 这里的类型必须是long, 两个类0和1
# 三种模式的损失函数
loss_f_none = nn.CrossEntropyLoss(weight=None, reduction='none')
loss_f_sum = nn.CrossEntropyLoss(weight=None, reduction='sum')
loss_f_mean = nn.CrossEntropyLoss(weight=None, reduction='mean')
# forward
loss_none = loss_f_none(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)
# view
print("Cross Entropy Loss:\n ", loss_none, loss_sum, loss_mean)
## 结果:
Cross Entropy Loss:
tensor([1.3133, 0.1269, 0.1269]) tensor(1.5671) tensor(0.5224)
这样可以看到, none模式下是输出三个损失, sum下是三个损失求和,mean下是三个损失求平均。这里还要注意一下这里的target, 这个是每个样本给出属于哪一个类即可,类型是torch.long, 为什么要强调这个,我们下面会学习二分类交叉熵损失,是交叉熵损失函数的特例,那里的target更要注意,对比起来更容易理解
下面我们再通过代码看看加上weight的损失:
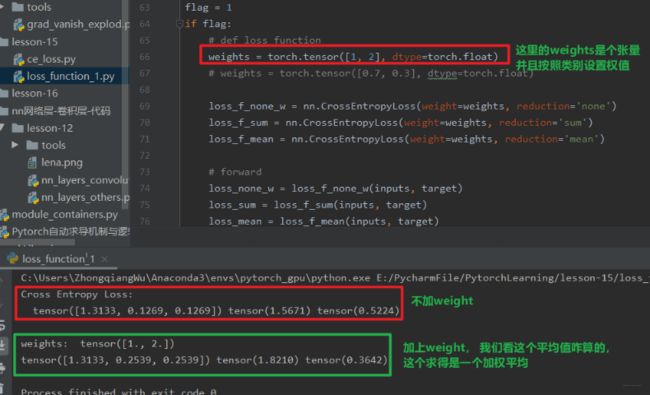
这里可以发现,给类别加上权值之后,对应样本的损失就会相应的加倍,这里重点是了解一下这个加上权之后,mean模式下怎么计算的损失: 其实也很简单,我们三个样本,第一个权值为1, 后两个权值为2, 所以分母不再是3个样本,而是1+2+2, 毕竟后两个样本权为2, 一个样本顶第一个的这样的2个。所以mean模式下求平均不是除以样本的个数,而是样本所占的权值的总份数。
3.2.1 还有几个交叉熵损失函数的特例
-
nn.NLLoss
在上面的交叉熵损失中,我们发现这个是softmax和NLLoss的组合,那么这里的nn.NLLLoss是何物啊? 交叉熵损失里面还有个这个东西,其实这个东西不要被这个名字给迷惑了, 这个就是实现了一个负号的功能:
nn.NLLoss: 实现负对数似然函数里面的负号功能

下面看看这个东西到底干啥用, 我这样测试了一下:
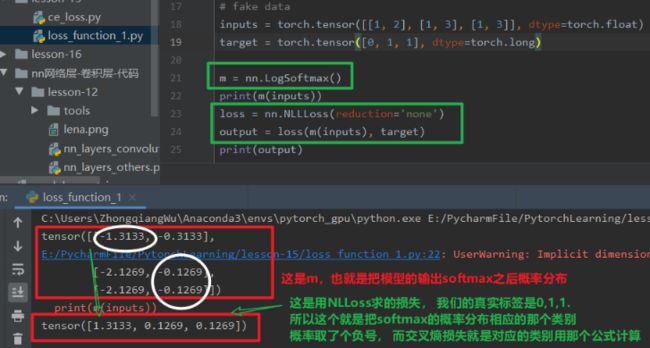
这个损失函数,就是根据真实类别去获得相应的softmax之后的概率结果,然后取反就是最终的损失。 还别说,真能反应模型好坏, 因为第一个类分错了,所以损失就大,看到没。 -
nn.BCELoss
这个是交叉熵损失函数的特例,二分类交叉熵。注意:输入值取值在[0,1]

这里的参数和上面的一样,也不说了, 看看这个计算公式吧:
l n = − w n [ y n ⋅ log x n + ( 1 − y n ) ⋅ log ( 1 − x n ) ] l_{n}=-w_{n}\left[y_{n} \cdot \log x_{n}+\left(1-y_{n}\right) \cdot \log \left(1-x_{n}\right)\right] ln=−wn[yn⋅logxn+(1−yn)⋅log(1−xn)]
逻辑回归的时候,是不是就是这个公式啊? 我们看看代码中这个怎么用:
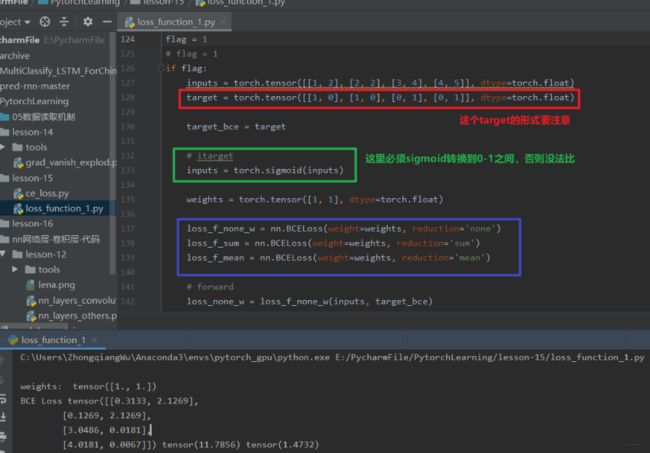
这里首先注意的点就是target, 这里可以发现和交叉熵那里的标签就不一样了,首先是类型是float, 每个样本属于哪一类的时候要写成独热的那种形式,这是因为看损失函数的计算公式也能看到,每个神经元一一对应的去计算loss,而不是一个整的神经元向量去计算loss, 看结果也会发现有8个loss,因为每个神经元都一一去计算loss,根据inputs,这里是两个神经元的。 -
nn.BCEWithLogitsLoss
这个函数结合了Sigmoid与二分类交叉熵,注意事项: 网络最后不加sigmoid函数
 这里的参数多了一个
这里的参数多了一个pow_weight, 这个是平衡正负样本的权值用的, 对正样本进行一个权值设定。比如我们正样本有100个,负样本有300个,那么这个数可以设置为3,在类别不平衡的时候可以用。计算公式如下:
l n = − w n [ y n ⋅ log σ ( x n ) + ( 1 − y n ) ⋅ log ( 1 − σ ( x n ) ) ] l_{n}=-w_{n}\left[y_{n} \cdot \log \sigma\left(x_{n}\right)+\left(1-y_{n}\right) \cdot \log \left(1-\sigma\left(x_{n}\right)\right)\right] ln=−wn[yn⋅logσ(xn)+(1−yn)⋅log(1−σ(xn))]
这里了就是加了个sigmoid。
3.3 剩余的14种损失函数介绍
-
nn.L1Loss
这个用于回归问题,用来计算inputs与target之差的绝对值
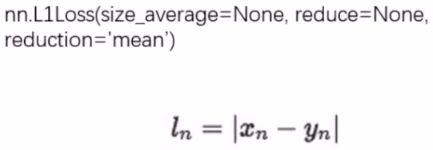
上面的size_average和reduce不用再关注,即将淘汰。 而reduction这个三种模式,其实和上面的一样。 -
nn.SmoothL1Loss
这是平滑的L1Loss(回归问题)

那么这个平滑到底是怎么体现的呢?

采用这种平滑的损失函数可以减轻离群点带来的影响。 -
nn.PoissonNLLLoss
功能: 泊松分布的负对数似然损失函数, 分类里面如果发现数据的类别服从泊松分布,可以使用这个损失函数

- log_intput: 输入是否为对数形式, 决定我们的计算公式。 若为True, l o s s ( i n p u t , t a r g e t ) = e x p ( i n p u t ) − t a r g e t × i n p u t loss(input, target) = exp(input) -target\times input loss(input,target)=exp(input)−target×input. 若为False, l o s s ( i n p u t , t a r g e t ) = i n p u t − t a r g e t × l o g ( i n p u t + e p s ) loss(input,target)=input-target\times log(input+eps) loss(input,target)=input−target×log(input+eps)
- full: 计算所有loss, 默认为False,这个一般不用管
- eps: 修正项, 避免log(input) 为nan
-
nn.KLDivLoss
功能:计算KLD, KL散度,相对熵,注意: 需要提前将输入计算log-probabilities, 如通过nn.logsoftmax()

其实这个已经在上面交叉熵的时候说完了。上面的Pytorch里面的计算和我们原来公式里面的计算还有点不太一样,所以我们得自己先logsoftmax(),完成转换为分布然后转成对数才可以。
这里的reduction还多了一种计算模式叫做batchmean, 是按照batchsize的大小求平均值。 -
nn.MarginRankingLoss
功能:计算两个向量之间的相似度,用于排序任务。 特别说明, 该方法计算两组数据之间的差异,也就是每个元素两两之间都会计算差异,返回一个n*n的loss矩阵。类似于相关性矩阵那种。

margin表示边界值, x1与x2之间的差异值。 这里的计算公式如下:loss ( x , y ) = max ( 0 , − y ∗ ( x 1 − x 2 ) + margin ) \operatorname{loss}(x, y)=\max (0,-y *(x 1-x 2)+\operatorname{margin}) loss(x,y)=max(0,−y∗(x1−x2)+margin)
- y=1时, 希望x1比x2大, 当x1>x2时,不产生loss
- y=-1时, 希望x2比x1大, 当x2>x1时, 不产生loss
-
nn.MultiLabelMarginLoss
功能:多标签边界损失函数, 这是一个多标签分类,就是一个样本可能属于多个类,和多分类任务还不一样。(多标签问题)

这个的计算公式如下:
loss ( x , y ) = ∑ i j max ( 0 , 1 − ( x [ y [ j ] ] − x [ i ] ) ) x ⋅ size ( 0 ) \operatorname{loss}(x, y)=\sum_{i j} \frac{\max (0,1-(x[y[j]]-x[i]))}{x \cdot \operatorname{size}(0)} loss(x,y)=ij∑x⋅size(0)max(0,1−(x[y[j]]−x[i]))
这里的i取值从0到输出的维度减1, j取值也是0到y的维度减1, 对于所有的i和j, i不等于y[j],也就是标签所在的神经元去减掉那些非标签所在的神经元,这说的啥? 一脸懵逼,还是看代码理解一下吧:
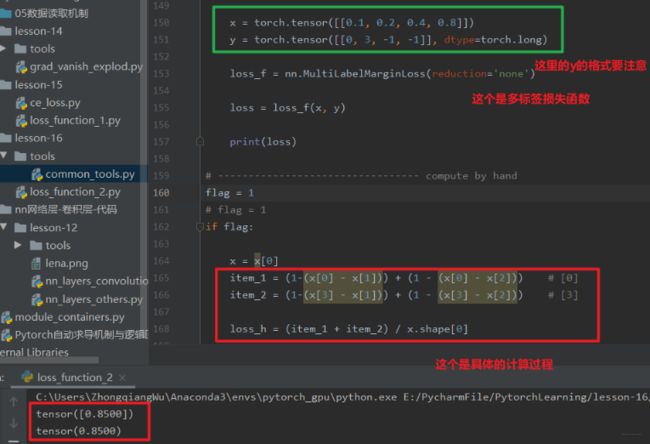
我们看上面这个代码, 假设我们有一个训练样本,输出层4个神经元,也就是4分类的问题,前向传播后,神经网络的四个神经元的输出分别是[0.1, 0.2, 0.4, 0.8], 而这个样本的真实标签是[0, 3, -1, -1], 首先解释这是啥意思,就是说这个样本属于第0类和第3类, 这个地方必须是torch.long型, 并且必须和输出神经元个数一样, 属于哪几类写前面,不够长度的用-1填补。 使用多标签边界损失函数的时候, 具体计算就是下面那样我们的输入样本属于0和3这两类, 不属于1和2, 那么就根据上面那个公式,后面那部分是标签所在的神经元减去标签不不在的神经元, 比如标签在第0个神经元:
- item_1 = (1-(x[0]-x[1])) + (1-(x[0]-x[2])) # 标签在第0个神经元的时候
- item_2 = (1-(x[3]-x[1])) + (1-(x[3]-x[2])) # 标签在第3个神经元的时候
- 然后就是这两部分的损失相加除以总的神经元个数: loss = (item_1+item_3) / x.shape[0]
应该差不多明白这个过程了,可以为啥要这么做呢? 这个意思就是说我们希望标签所在的神经元要比非标签所在的神经元的输出值要尽量的大,当这个差大于1了, 我们根据
max(0, 1-差值), 才发现不会有损失产生, 当这个差值小或者非标签所在的神经元比标签所在神经元大的时候,都会产生损失。 所以上面那个例子,我们想让第0个神经元的值要比第1个,第二个大一些,第3个神经元的值要比第1个,第2个大一些,这才能说明这个样本属于第0类和第3类,才是我们想要的结果啊。 有没有一点hinge loss的意思? 只不过那里是多分类,而这里是多标签分类,感觉思想差不多。 -
nn.SoftMarginLoss
功能: 计算二分类的logistic损失(二分类问题)

计算公式如下:
loss ( x , y ) = ∑ i log ( 1 + exp ( − y [ i ] ∗ x [ i ] ) ) x . nelement() \operatorname{loss}(x, y)=\sum_{i} \frac{\log (1+\exp (-y[i] * x[i]))}{x . \text { nelement()} } loss(x,y)=i∑x. nelement()log(1+exp(−y[i]∗x[i])) -
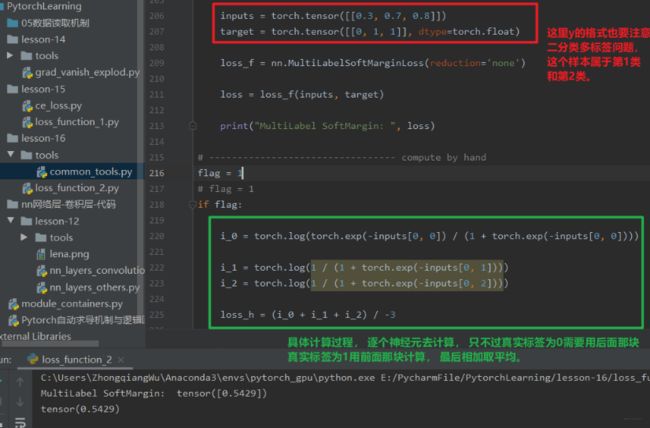
nn.MultiLabelSortMarginLoss
功能: SoftMarginLoss多标签版本 (多标签问题)
之类的weight,表示各类别的loss设置权值。计算公式如下:
loss ( x , y ) = − 1 C ∗ ∑ i y [ i ] ∗ log ( ( 1 + exp ( − x [ i ] ) ) − 1 ) + ( 1 − y [ i ] ) ∗ log ( exp ( − x [ i ] ) ( 1 + exp ( − x [ i ] ) ) ) \operatorname{loss}(x, y)=-\frac{1}{C} * \sum_{i} y[i] * \log \left((1+\exp (-x[i]))^{-1}\right)+(1-y[i]) * \log \left(\frac{\exp (-x[i])}{(1+\exp (-x[i]))}\right) loss(x,y)=−C1∗i∑y[i]∗log((1+exp(−x[i]))−1)+(1−y[i])∗log((1+exp(−x[i]))exp(−x[i])) -
nn.MultiMarginLoss(hingLoss)
功能: 计算多分类的折页损失(多分类问题)

这里的p可选1或者2, margin表示边界值。计算公式如下:
loss ( x , y ) = ∑ i max ( 0 , margin − x [ y ] + x [ i ] ) ) p x ⋅ size ( 0 ) \operatorname{loss}(x, y)=\frac{\left.\sum_{i} \max (0, \operatorname{margin}-x[y]+x[i])\right)^{p}}{x \cdot \operatorname{size}(0)} loss(x,y)=x⋅size(0)∑imax(0,margin−x[y]+x[i]))p
这里的x, y是0-神经元个数减1, 并且对于所以i和j, i不等于y[j]。这里就类似于hing loss了, 这里的x[y]表示标签所在的神经元, x[i]表示非标签所在的神经元。还是先看个例子,了解一下这个计算过程,然后借着这个机会也说一说hing loss吧:
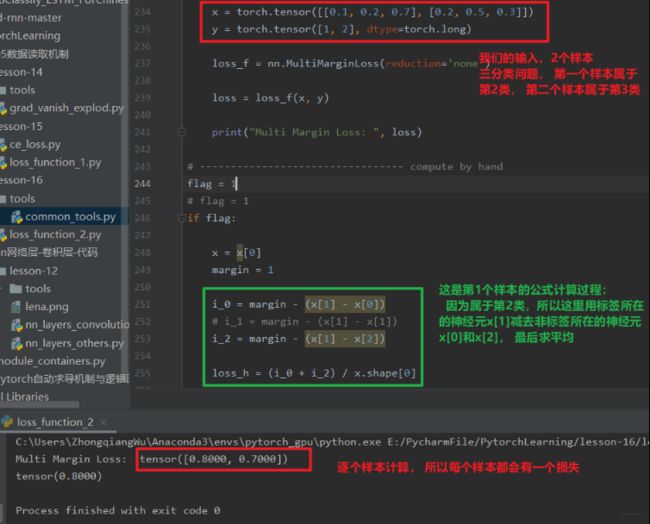
这个其实和多标签边界损失函数的原理差不多,只不过那里是一个样本属于多个类,需要每个类都这样算算,而这里一个样本属于1个类,只计算一次即可。这个其实就是我们的hinge loss损失,我们可以看一下:这个地方的原理啥的就先不推了:

假如我们现在有三个类别, 而得分函数计算某张图片的得分为$f(x_i, W)=[13, -7, 11], 而实际结果是第一类( y i = 0 y_i=0 yi=0 )。 假设 Δ = 10 \Delta=10 Δ=10,这个就是上面的margin,那么上面的公式就把错误类别( j ≠ y i ) j \neq y_i) j=yi)都遍历了一遍,求值加和:
L i = max ( 0 , − 7 − 13 + 10 ) + max ( 0 , 11 − 13 + 10 ) L_{i}=\max (0,-7-13+10)+\max (0,11-13+10) Li=max(0,−7−13+10)+max(0,11−13+10)
这个损失和交叉熵损失是不同的两种评判标准,这个损失聚焦于分类错误的与正确类别之间的惩罚距离越小越好,而交叉熵损失聚焦分类正确的概率分布越大越好。 -
nn.TripletMarginLoss
功能: 计算三元组损失, 人脸验证中常用

这里的p表示范数的阶。计算公式:
L ( a , p , n ) = max { d ( a i , p i ) − d ( a i , n i ) + margin , 0 } L(a, p, n)=\max \left\{d\left(a_{i}, p_{i}\right)-d\left(a_{i}, n_{i}\right)+\operatorname{margin}, 0\right\} L(a,p,n)=max{d(ai,pi)−d(ai,ni)+margin,0}
三元组在做这么个事情, 我们在做人脸识别训练模型的时候,往往需要把训练集做成三元组(A, P, N), A和P是同一个人, A和N不是同一个, 然后训练我们的模型

我们想让模型把A和P看成一样的,也就是争取让A和P之间的距离小,而A和N之间的距离大,那么我们的模型就能够进行人脸识别任务了。 -
nn.HingeEmbeddingLoss
功能: 计算两个输入的相似性, 常用于非线性embedding和半监督学习。 特别注意, 输入的x应为两个输入之差的绝对值, 也就是手动计算两个输入的差值

计算公式如下:
l n = { x n , if y n = 1 max { 0 , Δ − x n } , if y n = − 1 l_{n}=\left\{\begin{array}{ll} x_{n}, & \text { if } y_{n}=1 \\ \max \left\{0, \Delta-x_{n}\right\}, & \text { if } y_{n}=-1 \end{array}\right. ln={xn,max{0,Δ−xn}, if yn=1 if yn=−1 -
nn.CosineEmbeddingLoss
功能: 采用余弦相似度计算两个输入的相似性,常用于半监督学习和embedding

这里的margin可取值[-1, 1], 推荐为[0,0.5].计算公式如下:
loss ( x , y ) = { 1 − cos ( x 1 , x 2 ) , if y = 1 max ( 0 , cos ( x 1 , x 2 ) − margin ) , if y = − 1 \operatorname{loss}(x, y)=\left\{\begin{array}{ll} 1-\cos \left(x_{1}, x_{2}\right), & \text { if } y=1 \\ \max \left(0, \cos \left(x_{1}, x_{2}\right)-\operatorname{margin}\right), & \text { if } y=-1 \end{array}\right. loss(x,y)={1−cos(x1,x2),max(0,cos(x1,x2)−margin), if y=1 if y=−1
之所以用cos, 希望关注于这两个输入方向上的一个差异,而不是距离上的差异,cos函数如下:
cos ( θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ∑ i = 1 n A i × B i ∑ i = 1 n ( A i ) 2 × ∑ i = 1 n ( B i ) 2 \cos (\theta)=\frac{A \cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^{n} A_{i} \times B_{i}}{\sqrt{\sum_{i=1}^{n}\left(A_{i}\right)^{2}} \times \sqrt{\sum_{i=1}^{n}\left(B_{i}\right)^{2}}} cos(θ)=∥A∥∥B∥A⋅B=∑i=1n(Ai)2×∑i=1n(Bi)2∑i=1nAi×Bi -
nn.CTCLoss
功能: 计算CTC损失, 解决时序类数据的分类

blank: blank label, zeor_infinity: 无穷大的值或者梯度置0, 这个使用起来比较复杂,所以具体的可以看看官方文档。
到这里,18种损失函数就介绍完了,哇,太多了,这哪能记得住啊, 所以我们可以对这些损失函数从任务的角度分分类,到时候看看是什么任务,然后看看有哪些损失函数可以用,再去查具体用法就可以啦。 我这边是这样分的:
- 分类问题
- 二分类单标签问题:
nn.BCELoss,nn.BCEWithLogitsLoss,nn.SoftMarginLoss - 二分类多标签问题:
nn.MultiLabelSoftMarginLoss - 多分类单标签问题:
nn.CrossEntropyLoss,nn.NLLLoss,nn.MultiMarginLoss - 多分类多标签问题:
nn.MultiLabelMarginLoss, - 不常用:
nn.PoissonNLLLoss,nn.KLDivLoss
- 二分类单标签问题:
- 回归问题:
nn.L1Loss,nn.MSELoss,nn.SmoothL1Loss - 时序问题:
nn.CTCLoss - 人脸识别问题:
nn.TripletMarginLoss - 半监督Embedding问题(输入之间的相似性):
nn.MarginRankingLoss,nn.HingeEmbeddingLoss,nn.CosineEmbeddingLoss
4. 总结
今天的内容就到这里了,这次整理的内容还是比较多的, 主要分为两大块:权重初始化和损失函数的介绍, 第一块里面有10中权重初始化方法,而第二块里面18种损失函数。 哇,这个知识量还是很大的,当然我们其实并不需要都记住,只知道有哪些方法,具体什么时候用就行了,这个系列的目的也不是要求一下子都会了, 而是先有个框架出来。 快速梳理一遍吧:
首先,我们解决了模型模块的小尾巴, 权重的初始化方法,我们学习了梯度消失和梯度爆炸的原理,也知道了权重初始化的重要性,针对各种情况学习了不同的初始化方法,重要的是Xavier初始化和Kaiming初始化方法, 分别针对非饱和激活函数和包含激活函数的网络。
然后学习了损失函数的相关知识,通过损失函数的初步介绍,我们知道了损失函数也是一个Module,那么初始化和运行机制就基本了解。 然后学习了交叉熵损失函数及四个特例, 交叉熵损失函数比较重要,所以学习了一下原理,从自信息,熵,相对熵到交叉熵都过了一遍。 最后又根据场景的不同学习了其他14种损失函数。
下面依然是一个思维导图把知识拎起来,方便后面的速查:

好了,损失函数模块到这里就结束了,后面进入优化器部分, 我们还是那个流程:数据模块 -> 模型模块 -> 损失函数模块 -> 优化器 -> 迭代训练。 我们已经完成了3个模块的学习,马上就要看到曙光,再坚持一下, rush
PS: 本次学习视频来自B站https://www.bilibili.com/video/BV1EE41177ot?from=search&seid=13894259699897815176, 时间长了有可能被和谐了。 所有代码链接:
链接:https://pan.baidu.com/s/1c5EYdd0w8j6w3g54KTxJJA
提取码:k7rh