Transformer Assemble（PART III）

本文首发于微信公众号：NewBeeNLP，欢迎关注获取更多干货资源。

这一期魔改Transformers主要关注对原始模型中位置信息的讨论与优化，

• Self-Attention with RPR from Google，NAACL2018
• Self-Attention with SPR from Tencent，EMNLP 2019
• TENER from FDU
• Encoding Word Order in Complex Embedding，ICLR2020

1、Self-Attention with Relative Position Representations

一篇短文不是很难理解，文章要解决的痛点也非常清晰：self-attention机制在处理序列输入时无法编码位置信息。在原始Transformer里是采取sin/cos函数显示地引入位置信息，考虑的是绝对位置：
$$\begin{array}{rl}& PE(\text{pos},2i)=\sin \left(\frac{\text{pos}}{100000^{2i/d_{\text{nodd}}}}\right)\\ & PE(\text{ pos },2i+1)=\cos \left(\frac{\text{ pos }}{10000^{2i/d_{\text{nodd}}}}\right)\end{array}$$其中，$pos$表示token在序列中的位置，$i$表示position embedding的第$i$维，总共有$d_{model}$维。另外，作者在原文中指出，sin/cos函数的周期性形式可以允许模型进一步学习到相对位置的信息。但是这种方式学习到的相对位置信息仍然是存在较大缺陷的，参考文章【浅谈 Transformer-based 模型中的位置表示】。

正对以上问题，这篇论文提出一种相对位置信息引入Transformer的方法。

Vanilla Transformer

为了方便两者的对比，给出原始Transformer里self-attention的计算：
$$z_i=\sum _{j=1}^n{\alpha }_{ij}\left(x_j{W}^V\right)$$$${\alpha }_{ij}=\frac{\exp e_{ij}}{{\sum }_{k=1}^n\exp e_{ik}}$$$$e_{ij}=\frac{\left(x_i{W}^Q\right){\left(x_j{W}^K\right)}^T}{\sqrt{d_z}}$$

$e_{ij}$: the scaled dot product of token $i$ and token $j$;
${\alpha }_{ij}$: the weight coefficient of token $i$ and token $j$;
$zi$: the output representation of token $i$

Relative Position Representations

输入被看成是有向全连接图，两个token $x_i$、$x_j$之间的边设置了权重$a_{ij}^V,a_{ij}^K\in {\mathbb{R}}^{d_a}$，用做attention时key-value对添加相对位置信息。

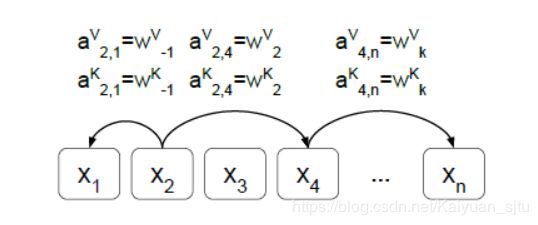
作者认为，在token之间超过一定距离之后相对位置信息就没有意义，因此设置了一个最大截断$k$，且截断可以更好地提升模型泛化能力。计算公式如下：
$$\begin{array}{rl}{a}_{ij}^K& =w_{\mathrm{clip}(j-i,k)}^K\\ a_{ij}^V& =w_{\mathrm{clip}(j-i,k)}^V\\ \mathrm{clip}(x,k)& =\max (-k,\min (k,x))\end{array}$$其中，上面的$a_{ij}^K$和$a_{ij}^V$都是需要学习的，即需要学习的为$$w^K=\left(w_{-k}^K,\dots ,w_k^K\right)\text{ and }{w}^V=\left(w_{-k}^V,\dots ,w_k^V\right)$$公式可能不好理解，举个栗子，假设序列长度N=9，截断窗口k=3，则RPR嵌入的lookup表如下图，感觉跟滑动窗口有点像：
$$w^K=\left(w_{-4}^K,\dots ,w_4^K\right)$$ $$w^V=\left(w_{-4}^V,\dots ,w_4^V\right)$$

Relation-aware Self-Attention

理解上面RPR之后，就可以对原始self-attention进行改写，将相对位置信息融入进去：
$$z_i=\sum _{j=1}^n{\alpha }_{ij}\left(x_j{W}^V+a_{ij}^V\right)$$$$e_{ij}=\frac{x_i{W}^Q{\left(x_j{W}^K+a_{ij}^K\right)}^T}{\sqrt{d_z}}$$
虽然论文基本概念相对简单(自注意力机制中包含了相对位置信息)，但是它极大地提高了两个机器翻译任务的翻译质量。

Reference

• Code Here
• How Self-Attention with Relative Position Representations works

---

---

Self-Attention with Structural Position Representations

不管是transformer原文的绝对位置编码还是上文引入的相对位置编码，都属于sequential information。作者从Hewitt和Manning发表的论文中得到启发：句子的潜在结构可以通过结构深度和距离来捕获，于是他们提出了absolute structural position来编码元素在句法树种深度，relative structural position来编码元素之间的距离。

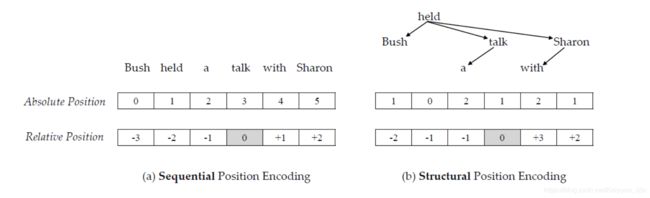
上图左边属于两种序列位置编码表示，具体在上一节已经有介绍；右边是本文提出的结构位置编码，分为两种：

• Absolute Structural Position：把句子的主要动词(如上图"held")作为origin，然后通过计算句法树中目标词语origin之间的距离作为绝对结构位置信息：
  $${\mathrm{abs}}_{\mathrm{str}u}\left(x_i\right)={\mathrm{distance}}_{\mathrm{tree}}\left(x_i,\text{origin}\right)$$
• Relative Structural Position：相对位置信息考虑的单词对之间的关系，
  • 如果单词$x_i$和$x_j$在句法树的同一条边上，则相对位置即为绝对位置之差：
    $$re{l}_{stru}\left(x_i,x_j\right)=ab{s}_{stru}\left(x_i\right)-ab{s}_{stru}\left(x_j\right)$$
  • 如果在不同的边上，相对位置为绝对位置之和乘上一个系数$f_{stru}(x)$
    $$re{l}_{stru}\left(x_i,x_j\right)=f_{stru}(i-j)\ast \left(ab{s}_{stru}\left(x_i\right)+ab{s}_{stru}\left(x_j\right)\right)$$当两个单词正序时系数为1；相同时系数为0；逆序时系数为-1：
    $$f_{stru}(x)=\{\begin{array}{ll}1& x>0\\ 0& x=0\\ -1& x<0\end{array}$$

接下去就是将结构位置信息整合进SAN，

• 对于绝对位置，通过一个非线性函数将序列位置和结构位置融合得到位置表示：
  $$\mathrm{asb}\left(x_i\right)=f_{abs}(\mathrm{A}\mathrm{B}\mathrm{S}\mathrm{P}\mathrm{E}\left(ab{s}_{seq}\right),\mathrm{A}\mathrm{B}\mathrm{S}\mathrm{P}\mathrm{E}\left(ab{s}_{stru}\right))$$
• 对于相对位置，采用同上一篇论文一致的方法

一点疑问…
简单看了一下《A Structural Probe for Finding Syntax in Word Representations》，也就是作者在文章里说给了他们motivation的论文，大概说的是通过structural probe检测像BERT这样的模型学到的context represetation是否包含了syntax tree信息，结论是可以学到句法树的结构信息。那这样为啥还要加structural position representation呢？

---

TENER: Adapting Transformer Encoder for Named Entity Recognition

针对命名实体识别任务的一个工作，虽然Transformer系在NLP很多领域都取得了非常大的进步，但是在NER任务上表现不佳。作者分析了注意力机制与特定的NER任务，发现原始实现中的位置信息编码、注意力稀疏性方面不太适用于NER。

位置信息编码

• 距离性
  vanilla transformer中位置信息使用sin/cos函数嵌入，由公式定义
  $$\begin{array}{rl}P{E}_{t,2i}=& \sin \left(\frac{t}{10000^{2i/d}}\right)\\ P{E}_{t,2i+1}& =\cos \left(\frac{t}{10000^{2/d}}\right)\end{array}$$可以推导出$$\begin{array}{rl}P{E}_t^{T}P{E}_{t+k}& =\sum _{j=0}^{\frac{d}{2}-1}\left[\sin \left(c_{j}t\right)\sin \left(c_j(t+k)\right)+\cos \left(c_{j}t\right)\cos \left(c_j(t+k)\right)\right]\\ & =\sum _{j=0}^{\frac{d}{2}-1}\cos \left(c_j(t-(t+k))\right)\\ & =\sum _{j=0}^{\frac{d}{2}-1}\cos \left(c_{j}k\right)\end{array}$$可见两个元素的点积只与它们之间的距离$k$有关（距离敏感），但是进一步研究可以发现，当position embedding被映射到自注意力的键值对时，其就会失去距离敏感性，如下图，最上面的曲线表示$P{E}_t^{T}P{E}_{t+k}$，可以反映对称性；下面两条曲线表示$P{E}_t^{T}WP{E}_{t+k}$，无距离特性。
  

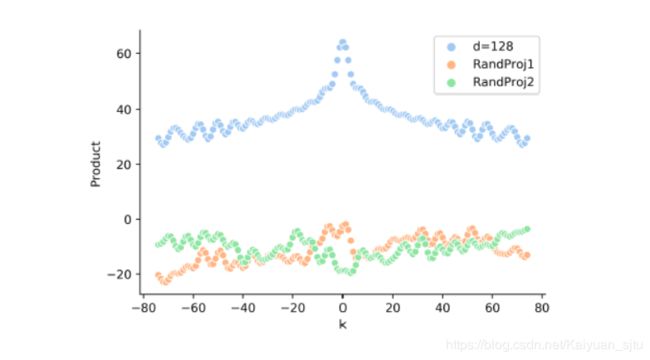
论文中说$P{E}_t^{T}WP{E}_{t+k}$中的$W$是随机的，但是这个参数是可学习的，在模型训练之后会不会效果变好？

• 方向性
  此外，由上述推导可知，令$j=t-k$，有
  $$P{E}_t^{T}P{E}_{t+k}=P{E}_j^{T}P{E}_{j+k}=P{E}_{t-k}^{T}P{E}_t$$因此这也是方向不敏感的

由上分析可知该种嵌入方式并不能反映方向性和距离性，但是对于NER任务而言距离和方向都是尤为重要的。为此本文对注意力分数计算进行改进，将绝对位置改成相对位置：$$Q,K,V=H{W}_q,H_{d_k},H{W}_v$$$$R_{t-j}={\left[\dots ,\sin \left(\frac{t-j}{10000^{2i}{d}_k}\right)\cos \left(\frac{t-j}{10000^{2i}{d}_k}\right),\dots \right]}^T$$$$A_{tj}^{rel}=Q_t^T{K}_j+Q_t^T{R}_{t-j}{u}^T{K}_j+v^T{R}_{t-j}$$$$Attn(Q,K,V)=\mathrm{softmax}\left(A^{rel}\right)V$$与transformer-xl里的比较像。

注意力稀疏

注意到修改后的Attention计算最后没有用到scaling系数$\sqrt{d}$，这是因为对于NER任务只需要attend几个相对重要的context就足够了，scaled后的attention分布过于平滑会引入噪音。

这篇论文感觉主要重点在工程意义，在NER任务达到最好的效果；针对NER任务做了专门的修改，除了上面的相对位置信息和系数注意力，由于NER数据集相对较小，也减少了模型的可学习参数避免过拟合。

reference

• Code Here
• TENER: Adapting Transformer Encoder for NER

---

---

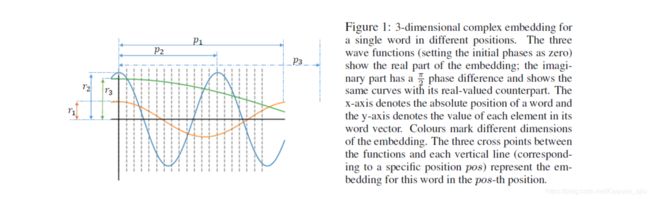
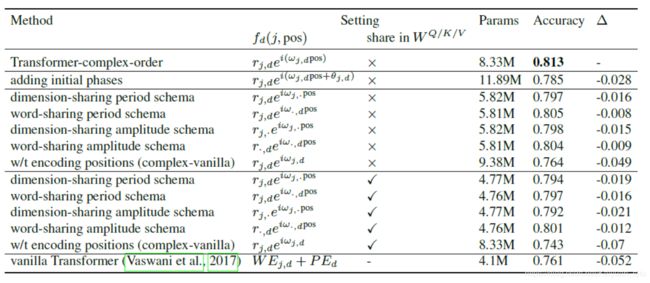
Encoding Word Order in Complex Embedding

比较有意思的工作，关注的点也是在序列建模的位置信息编码。先前的方法通过引入额外的位置编码，在embedding层将词向量和位置向量通过加性编码融合，
$$f(j,pos)=f_{we}(j)+f_{pe}(pos)$$但是该种方式每个位置向量是独立训练得到的，并不能建模序列的order relationship（例如邻接或优先关系），作者将此称为the position independece problem。

针对该问题提出了一种新的位置编码方式，将独立的词向量替换成自变量为位置的函数，于是单词表示会随着位置的变化而平滑地移动，可以更好地建模单词的绝对位置和顺序信息。
$$f(j,\text{ pos })=g_j(\text{ pos })\in {\mathbb{C}}^D$$其中，$f(j,\text{ pos })$表示此表中序号为$j$的单词在位置$pos$时的单词向量，$D$表示函数集合，$g_{we}(\cdot ):\mathbb{N}\to (\mathcal{F}{)}^D$表示单词到函数的映射，展开即为，$$\left[g_{j,1}(\mathrm{p}\mathrm{o}\mathrm{s}),g_{j,2}(\mathrm{p}\mathrm{o}\mathrm{s}),\dots ,g_{j,D}(\mathrm{p}\mathrm{o}\mathrm{s})\right]\in {\mathbb{C}}^D$$
为了达到上述要求，函数应该满足以下两个条件：

Property 1. Position-free offset transformation

对于任意位置pos和$n>1$，存在变换Transform ${}_n(\cdot )=$ Transform $(n,\cdot )$满足，$$g(\mathrm{p}\mathrm{o}\mathrm{s}+n)={\text{ Transform }}_n(g(\mathrm{p}\mathrm{o}\mathrm{s}))$$特别地，论文考虑Transform为线性变换

Property 2. Boundedness

函数应该是有界的，
$$\exists \delta \in {\mathbb{R}}^{+},\forall \text{ pos }\in \mathbb{N},|g(\mathrm{pos})|\le \delta$$
接下去，论文证明了满足上述两个条件的解函数形式为，
$$g(pos)=z_2{z}_1^{pos}\text{ for }{z}_1,z_2\in \mathbb{C}\text{ with }\left|z_1\right|\le 1$$

贴一下论文给的证明：（看不看无所谓，能用就行haha）
假设函数$g$满足上述两个条件，则对于任意位置$n_1,n_2\in \mathbb{N}$，有
$$\begin{array}{rl}w\left(n_1\right)w\left(n_2\right)g(\text{ pos })& =w\left(n_2\right)g\left(\text{ pos }+n_1\right)=g\left(\text{ pos }+n_1+n_2\right)\\ & ={\text{ Transform }}_{n_1+n_2}(g(\text{ pos }))=w\left(n_1+n_2\right)g(\text{ pos })\end{array}$$因此有$w\left(n_1+n_2\right)=w\left(n_1\right)w\left(n_2\right)$。我们令$w(1)=z_1$以及$g(0)=z_2$，由于$n_1,n_2\in \mathbb{N}$是任意的，有
$$w(n)=(w(1){)}^n=z_1^n$$$$g(\text{ pos }+n)=w(n)g(\text{ pos })=z_1^{n}g(\text{ pos })$$当pos $\ge 1$时，有
$$g(\text{ pos })=g(1+\text{ pos }-1)=w(\text{ pos })g(0)=z_1^{\text{pos }}{z}_2=z_2{z}_1^{\text{pos }}$$
当pos $=1$时，有$$g(0)=z_2=z_2{z}_1^0$$综上，将上述所有情况综合有$$g(\text{ pos })=z_2{z}_1^{\text{pos }}$$发现当$\left|z_1\right|>1$，$g(\text{ pos })$就不是有界的了，因此限制$\left|z_1\right|\le 1$后，有
$$|g(\text{ pos })|\le |z_2{z}_1^{\text{pos }}|\le |z_2||z_1^{\text{pos }}|\le |z_2|$$这样就满足有界性的条件了；
又由$w(n)=z_1^n$和Transform ${}_n(\text{ pos })=w(n)$ pos得对所有的位置pos，$$g(\text{ pos }+n)=z_2{z}_1^{\mathrm{p}\mathrm{s}+n}=z_2{z}_1^{\mathrm{p}\mathrm{o}\mathrm{s}}{z}_1^n=g(\text{ pos })z_1^n={\text{Transform}}_n(g(\text{ pos }))$$
得证

根据欧拉公式，可以将上式转化为，
$$g(\text{ pos })=z_2{z}_1^{\text{pos }}=r_2{e}^{i{\theta }_2}{\left(r_1{e}^{i{\theta }_1}\right)}^{\text{pos }}=r_2{r}_1^{\text{pos }}{e}^{i\left({\theta }_2+{\theta }_1\text{ pos }\right)}\text{ subject to }\left|r_1\right|\le 1$$在实现过程中，由于上述$\left|r_1\right|\le 1$的限制会导致优化问题，因此一种自然而然的做法就是固定$r_1=1$，于是上式可以简化为，$$g(\text{ pos })=r{e}^{i(\omega \text{ pos }+\theta )}$$
最终的embedding表示为，
$$f(j,\text{ pos })={\mathbf{g}}_j(\text{ pos })={\mathbf{r}}_j{e}^{i\left({\mathbf{\omega }}_j\text{ pos }+{\mathbf{\theta }}_j\right)}$$其中振幅$r_j$、角频率$w_j$和初相${\theta }_j$是需要学习的参数。

• 振幅$r_j$只和单词本身有关，即原本的词向量；
• 角频率$w_j$决定单词对位置的敏感程度。当角频率非常小时（如下图p1），单词对于所有位置的词向量基本保持不变，这就与标准词向量一样了；

简单看一下文本分类任务的消融性分析结果：

• 增加可学习初相之后效果比设置初相为0差：

  “The negative effect of initial phases may be due to periodicity, and $w$ cannot be directly regularized with L2-norm penalties.”

• 设置参数共享之后效果变差，可能是由于参数变少导致学习表征能力下降；
  

1. 要用的话，计算量以及参数量是不是会很大呀
2. 好像也没跟其他relative position的模型比较

reference

• Code Here
• Open Review