Leetcode之最长公共子串

问题描述：

编写一个函数来查找字符串数组中最长的公共前缀字符串。

如果没有公共前缀，则返回空字符串""。

例1：

输入： ["flower","flow","flight"]
 输出： “fl”

例2：

输入： [“dog”，“racecar”，“car”]
 输出： “”
 说明：输入字符串中没有公共前缀。

注意：

所有给定的输入都是小写字母a-z。

方法1：水平扫描

low就是low，没错我最后就是用这种方法解决的，也是解决方法中最差的，捂脸，还是有待提高啊。

这种想法主要是LCP(S1​…Sn​)=LCP(LCP(LCP(S1​,S2​),S3​),…Sn​)

基于这种迭代想法，从左到右遍历字符串（S1,S2...Sn），在每次迭代中找到最长公共前缀，当最长公共前缀是空时结束，返回空串，否则返回LCP(S1​…Sn​)

 public String longestCommonPrefix(String[] strs) {
    if (strs.length == 0||strs==null) return "";
    String prefix = strs[0];
    for (int i = 1; i < strs.length; i++)
        while (strs[i].indexOf(prefix) != 0) {
            prefix = prefix.substring(0, prefix.length() - 1);
            if (prefix.isEmpty()) return "";
        }        
    return prefix;
}

方法2：垂直扫描

想象一下，一个非常短的字符串位于数组的末尾。上述方法仍将如此比较字符串是不合理的。优化此案例的一种方法是进行垂直扫描。我们在移动到下一列之前，在同一列（字符串的相同字符索引）上从上到下比较字符。

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";
    for (int i = 0; i < strs[0].length() ; i++){
        char c = strs[0].charAt(i);
        for (int j = 1; j < strs.length; j ++) {
            if (i == strs[j].length() || strs[j].charAt(i) != c)
                return strs[0].substring(0, i);             
        }
    }
    return strs[0];
}

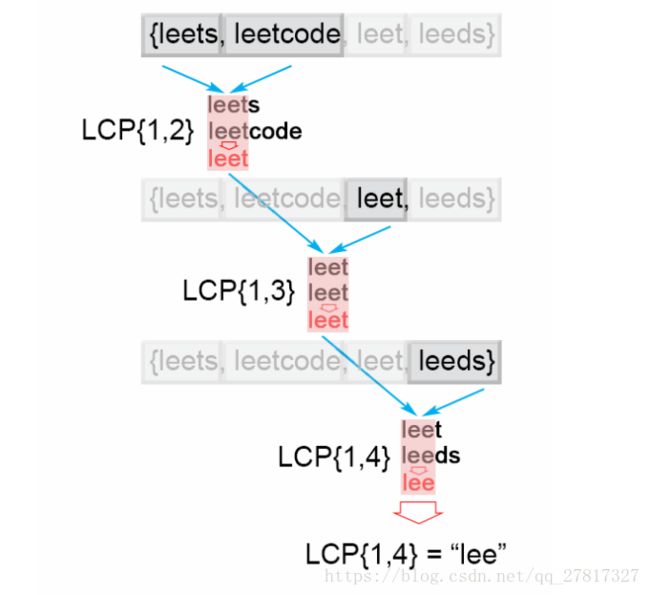
方法3：分而治之

算法的思想来自于LCP操作的关联属性。我们注意到LCP(S1​…Sn​)=LCP(LCP(S1​…Sk​),LCP(Sk+1​…Sn​))

为了应用这种方案，我们采用分而治之的想法分裂问题LCP(Si​…Sj​)，将其分裂为LCP(Si…Smid)和LCP(Smid+1​…Sj)(其中mid= (i+j)/2),我们使用他们的解决方案lcpLeft并lcpRight构建主要问题的解决方案LCP(Si…Sj​).为了实现这一点，我们逐个比较角色lcpLeft和lcpRight直到没有角色匹配。找到的公共前缀lcpLeft和lcpRight就是解决方案 LCP(Si​…Sj​)。

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";    
        return longestCommonPrefix(strs, 0 , strs.length - 1);
}

private String longestCommonPrefix(String[] strs, int l, int r) {
    if (l == r) {
        return strs[l];
    }
    else {
        int mid = (l + r)/2;
        String lcpLeft =   longestCommonPrefix(strs, l , mid);
        String lcpRight =  longestCommonPrefix(strs, mid + 1,r);
        return commonPrefix(lcpLeft, lcpRight);
   }
}

String commonPrefix(String left,String right) {
    int min = Math.min(left.length(), right.length());       
    for (int i = 0; i < min; i++) {
        if ( left.charAt(i) != right.charAt(i) )
            return left.substring(0, i);
    }
    return left.substring(0, min);
}

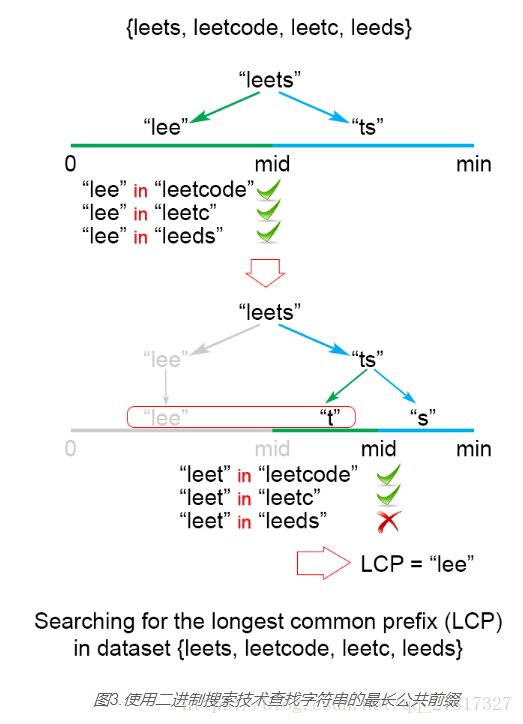
方法4：二进制查找

我们的想法是应用二进制搜索方法来查找具有最大值的字符串L，这是所有字符串的通用前缀。算法搜索空间是（0...minLen），其中minLen最小字符串长度和最大可能公共前缀。每次搜索空间被划分为两个相等的部分时，其中一个被丢弃，因为它确定它不包含解决方案。有两种可能的情况： 不是公共字符串，这意味着每个都不是公共字符串，我们丢弃搜索空间的后半部分。 是公共字符串，这意味着因为每个都是一个公共字符串而我们丢弃了搜索空间的前半部分，因为我们试图找到更长的公共前缀。

附上大神代码

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0)
        return "";
    int minLen = Integer.MAX_VALUE;
    for (String str : strs)
        minLen = Math.min(minLen, str.length());
    int low = 1;
    int high = minLen;
    while (low <= high) {
        int middle = (low + high) / 2;
        if (isCommonPrefix(strs, middle))
            low = middle + 1;
        else
            high = middle - 1;
    }
    return strs[0].substring(0, (low + high) / 2);
}

private boolean isCommonPrefix(String[] strs, int len){
    String str1 = strs[0].substring(0,len);
    for (int i = 1; i < strs.length; i++)
        if (!strs[i].startsWith(str1))
            return false;
    return true;
}

 进一步的思考/跟进

给定一组键S = [ S1，S2,...Sñ]，找到字符串q和S中最长的公共前缀。此LCP查询将被频繁调用。

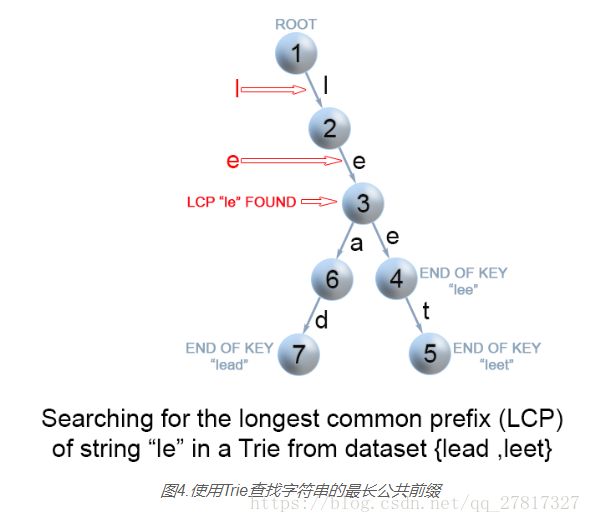
我们可以通过将一组键S存储在Trie中来优化LCP查询.在Trie中，从根开始的每个节点表示某些键的公共前缀。但是我们需要找到字符串q和所有键字符串的最长公共前缀。这意味着我们必须从根找到最深的路径，它满足以下条件： 它是查询字符串的前缀，q 沿路径的每个节点必须只包含一个子元素。否则，找到的路径将不是所有字符串中的公共前缀。*路径不包含标记为密钥结尾的节点。否则，路径不能是比其自身短的密钥的前缀a。

剩下的唯一问题是如何找到满足上述要求的Trie中最深的路径。最有效的方法是从中构建一个特定[S1...Sn]字符串。然后q在Trie中找到查询字符串的前缀。我们从根部穿过Trie，直到不可能继续Trie中的路径，因为上述条件之一不满足。

 思想就是这样，关于trie树的实现，之后的文章有详细讲解，这里不过多介绍。

牛人还是多啊，加油！！！