python 数据分析实践--(1)收入预测分析
收入分析预测
- 说明:
- 1. 预览数据集,明确分析目的
- 2. 导入数据集,预处理数据
- 3. 探索数据背后的特征
- 3.1 数值型变量统计描述
- 3.2 离散型变量统计描述
- 3 .3 了解数据的分布形状
- 4. 数据建模
- 4.1 对离散变量重编码
- 4.2 拆分数据集
- 4.3 搭建模型
- 4.4 模型网格搜索法,探寻模型最佳参数
- 4.5 模型预测与评估
- 4.5.1 K近邻模型在测试集上的预测
- 4.5.2 K近邻网格搜索模型在测试集上的预测
- 4.5.3 GBDT模型在测试集上的预测
- 4.5.4 网格搜索的GBDT模型在测试集上的预测
- 5.实验总结
说明:
本文用途只做学习记录:
- 参考书籍:从零开始学Python数据分析与挖掘/刘顺祥著.—北京:清华大学出版社,2018
- 数据下载:链接:https://pan.baidu.com/s/1VhnNfUNgNLICIFRyrlteOg提取码:m1dl
1. 预览数据集,明确分析目的
通过Excel工具打开income文件,可发现该数据集一共有 32 561条样本数据,共有15个数据变量,其中9个离散型变量,6个数值型变量。数据项主要包括:年龄,工作类型,受教育程度,收入等,具体可见下面两个图:
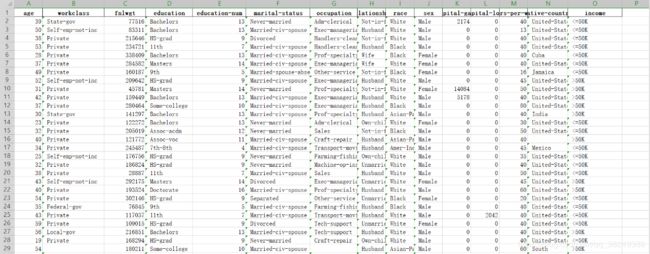
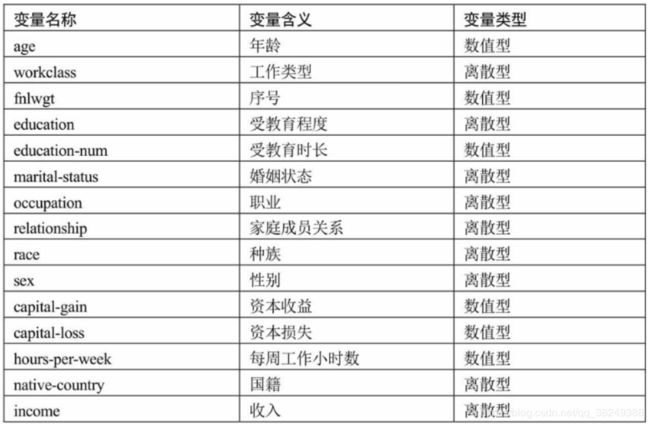
拿到上面的数据集,我们观察这些数据都有什么用,想一想这张数据表中income比较特殊,有分析价值,其他变量的不同会对income产生一定的影响。
实验目的:因此,基于上面的数据集,需要预测居民的年收入是否会超过5万美元?
2. 导入数据集,预处理数据
在jupyter notebook中导入相应包,读取数据,进行预处理。在上述数据集中,有许多变量都是离散型的,如受教育程度、婚姻状态、职业、性别等。通常数据拿到手后,都需要对其进行清洗,例如检查数据中是否存在重复观测、缺失值、异常值等,而且,如果建模的话,还需要对字符型的离散变量做相应的重编码。
import numpy as np
import pandas as pd
import seaborn as sns
# 下载的数据集存放的路径:
income = pd.read_excel(r'E:\Data\1\income.xlsx')
# 查看数据集是否存在缺失
income.apply(lambda x:np.sum(x.isnull()))
age 0
workclass 1836
fnlwgt 0
education 0
education-num 0
marital-status 0
occupation 1843
relationship 0
race 0
sex 0
capital-gain 0
capital-loss 0
hours-per-week 0
native-country 583
income 0
dtype: int64
从上面的结果可以发现,居民的收入数据集中有3个变量存在数值缺失,分别是居民的工作类型(离散型)缺1836、职业(离散型)缺1843和国籍(离散型)缺583。缺失值的存在一般都会影响分析或建模的结果,所以需要对缺失数值做相应的处理。
缺失值的处理一般采用三种方法:
- 1.删除法,缺失的数据较少时适用;
- 2.替换法,用常数替换缺失变量,离散变量用众数,数值变量用均值或中位数;
- 3.插补法:用未缺失的预测该缺失变量。
根据上述方法,三个缺失变量都为离散型,可用众数替换。pandas中fillna()方法,能够使用指定的方法填充NA/NaN值。
函数形式:
fillna(value=None, method=None, axis=None, inplace=False, limit=None, downcast=None, **kwargs)
参数:
-
value:用于填充的空值的值。(该处为字典)
-
method: {‘backfill’, ‘bfill’, ‘pad’, ‘ffill’, None}, default None。定义了填充空值的方法, pad/ffill表示用前面行/列的值,填充当前行/列的空值, backfill / bfill表示用后面行/列的值,填充当前行/列的空值。
-
axis:轴。0或’index’,表示按行删除;1或’columns’,表示按列删除。
-
inplace:是否原地替换。布尔值,默认为False。如果为True,则在原DataFrame上进行操作,返回值为None。
-
limit:int,default None。如果method被指定,对于连续的空值,这段连续区域,最多填充前 limit 个空值(如果存在多段连续区域,每段最多填充前 limit 个空值)。如果method未被指定, 在该axis下,最多填充前 limit 个空值(不论空值连续区间是否间断)
-
downcast:dict, default is None,字典中的项,为类型向下转换规则。或者为字符串“infer”,此时会在合适的等价类型之间进行向下转换,比如float64 to int64 if possible。
# 缺失值处理,采用众数替换法(mode()方法取众数)
income.fillna(value={'workclass':income['workclass'].mode()[0],
'ouccupation':income['occupation'].mode()[0],
'native-country':income['native-country'].mode()[0]},
inplace = True)
3. 探索数据背后的特征
对缺失值采用了替换处理的方法,接下来对居民收入数据集做简单的探索性分析,目的是了解数据背后的特征如数据的集中趋势、离散趋势、数据形状和变量间的关系等。首先,需要知道每个变量的基本统计值,如均值、中位数、众数等,只有了解了所需处理的数据特征,才能做到“心中有数”。
3.1 数值型变量统计描述
# 3.1 数值型变量统计描述
income.describe()
| age | fnlwgt | education-num | capital-gain | capital-loss | hours-per-week | |
|---|---|---|---|---|---|---|
| count | 32561.000000 | 3.256100e+04 | 32561.000000 | 32561.000000 | 32561.000000 | 32561.000000 |
| mean | 38.581647 | 1.897784e+05 | 10.080679 | 1077.648844 | 87.303830 | 40.437456 |
| std | 13.640433 | 1.055500e+05 | 2.572720 | 7385.292085 | 402.960219 | 12.347429 |
| min | 17.000000 | 1.228500e+04 | 1.000000 | 0.000000 | 0.000000 | 1.000000 |
| 25% | 28.000000 | 1.178270e+05 | 9.000000 | 0.000000 | 0.000000 | 40.000000 |
| 50% | 37.000000 | 1.783560e+05 | 10.000000 | 0.000000 | 0.000000 | 40.000000 |
| 75% | 48.000000 | 2.370510e+05 | 12.000000 | 0.000000 | 0.000000 | 45.000000 |
| max | 90.000000 | 1.484705e+06 | 16.000000 | 99999.000000 | 4356.000000 | 99.000000 |
上面的结果描述了有关数值型变量的简单统计值,包括非缺失观测的个数(count)、平均值(mean)、标准差(std)、最小值(min)、下四分位数(25%)、中位数(50%)、上四分位数(75%)和最大值(max)。
3.2 离散型变量统计描述
# 2. 离散型变量统计描述
income.describe(include= ['object'])
| workclass | education | marital-status | occupation | relationship | race | sex | native-country | income | |
|---|---|---|---|---|---|---|---|---|---|
| count | 32561 | 32561 | 32561 | 30718 | 32561 | 32561 | 32561 | 32561 | 32561 |
| unique | 8 | 16 | 7 | 14 | 6 | 5 | 2 | 41 | 2 |
| top | Private | HS-grad | Married-civ-spouse | Prof-specialty | Husband | White | Male | United-States | <=50K |
| freq | 24532 | 10501 | 14976 | 4140 | 13193 | 27816 | 21790 | 29753 | 24720 |
上面为离散变量的统计值,包含每个变量非缺失观测的数量(count)、不同离散值的个数(unique)、出现频次最高的离散值(top)和最高频次数(freq)。以受教育水平变量为例,一共有16种不同的教育水平;3万多居民中,高中毕业的学历是出现最多的;并且一共有10 501名。
3 .3 了解数据的分布形状
为了了解数据的分布形状(如偏度、峰度等)可以通过可视化的方法进行展现。
#以被调查居民的年龄和每周工作小时数为例,绘制各自的分布形状图:
import matplotlib.pyplot as plt
# 设置绘图风格
plt.style.use('ggplot')
# 设置多图形的组合
fig, axes = plt.subplots(3,1)
# 绘制不同收入水平下的年龄核密度图,观察连续型变量的分布情况
income.age[income.income == ' <=50K'].plot(kind = 'kde', label = '<=50K', ax = axes[0], legend = True, linestyle = '-')
income.age[income.income == ' >50K'].plot(kind = 'kde', label = '>50K', ax = axes[0], legend = True, linestyle = '--')
# 绘制不同收入水平下的周工作小时核密度图
income['hours-per-week'][income.income == ' <=50K'].plot(kind = 'kde', label = '<=50K', ax = axes[1], legend = True, linestyle = '-')
income['hours-per-week'][income.income == ' >50K'].plot(kind = 'kde', label = '>50K', ax = axes[1], legend = True, linestyle = '--')
# 绘制不同收入水平下的受教育时长核密度图
income['education-num'][income.income == ' <=50K'].plot(kind = 'kde', label = '<=50K', ax = axes[2], legend = True, linestyle = '-')
income['education-num'][income.income == ' >50K'].plot(kind = 'kde', label = '>50K', ax = axes[2], legend = True, linestyle = '--')

第一幅图展现的是,在不同收入水平下,年龄的核密度分布图,对于年收入超过5万美元的居民来说,他们的年龄几乎呈现正态分布,而收入低于5万美元的居民,年龄呈现右偏特征,即年龄偏大的居民人数要比年龄偏小的人数多。
第二幅图展现了不同收入水平下,周工作小时数的核密度图,很明显,两者的分布趋势非常相似,并且出现局部峰值。
第三幅图展现了不同收入水平下,教育时长的核密度图,很明显,两者的分布趋势非常相似,并且也多次出现局部峰值。
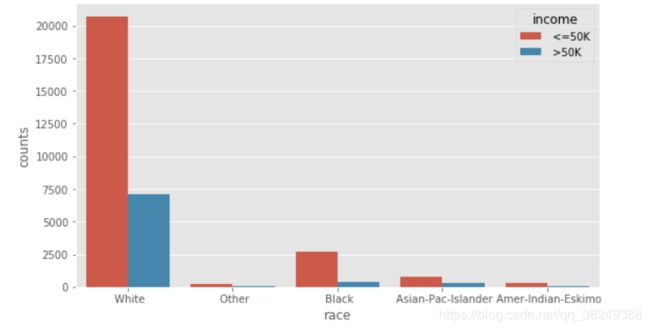
针对离散型变量,对比居民的收入水平高低在性别、种族状态、家庭关系等方面的差异,进而可以发现这些离散变量是否影响收入水平:
# 构造不同收入水平下各种族人数的数据
race = pd.DataFrame(income.groupby(by = ['race','income']).aggregate(np.size).loc[:,'age'])
#print(race)
# 重设行索引
race = race.reset_index()
#print(race)
# 变量重命名
race.rename(columns={'age':'counts'}, inplace=True)
#print(race)
# 排序
race.sort_values(by = ['race','counts'], ascending=False, inplace=True)
#print(race)
# 构造不同收入水平下各家庭关系人数的数据
relationship = pd.DataFrame(income.groupby(by = ['relationship','income']).aggregate(np.size).loc[:,'age'])
relationship = relationship.reset_index()
relationship.rename(columns={'age':'counts'}, inplace=True)
relationship.sort_values(by = ['relationship','counts'], ascending=False, inplace=True)
# 构造不同收入水平下各男女人数的数据
sex = pd.DataFrame(income.groupby(by = ['sex','income']).aggregate(np.size).loc[:,'age'])
sex = sex.reset_index()
sex.rename(columns={'age':'counts'}, inplace=True)
sex.sort_values(by = ['sex','counts'], ascending=False, inplace=True)
# 设置图框比例,并绘图
plt.figure(figsize=(9,5))
sns.barplot(x="race", y="counts", hue = 'income', data=race)
plt.show()
plt.figure(figsize=(9,5))
sns.barplot(x="relationship", y="counts", hue = 'income', data=relationship)
plt.show()
plt.figure(figsize=(9,5))
sns.barplot(x="sex", y="counts", hue = 'income', data=sex)
plt.show()
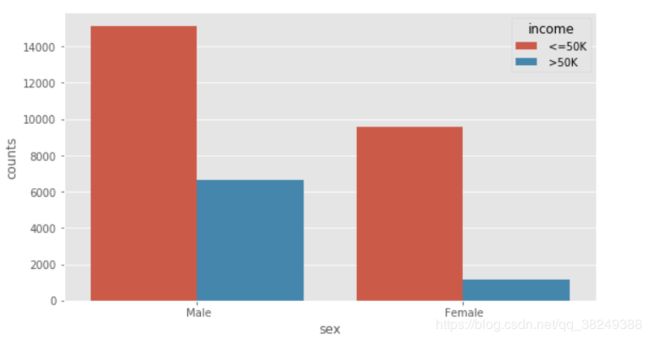
图一、反映的是相同的种族下,居民年收入水平高低的人数差异;图二、反映的是相同的家庭成员关系下,居民年收入水平高低的人数差异。但无论怎么比较,都发现一个规律,即在某一个相同的水平下(如白种人或未结婚人群中),年收入低于5万美元的人数都要比年收入高于5万美元的人数多,这个应该是抽样导致的差异(数据集中年收入低于5万和高于5万的居民比例大致在75%:25%)。图三、反映的是相同的性别下,居民收入水平高低人数的差异;其中,女性收入低于5万美元的人数比高于5万美元人数的差异比男性更严重,比例大致为90%:10%, 男性大致为70%:30%。
4. 数据建模
4.1 对离散变量重编码
由于数据集中有很多离散型变量,这些变量的值为字符串,不利于建模,因此,需要先对这些变量进行重新编码。编码的方法有很多种:
- 将字符型的值转换为整数型的值
- 哑变量处理(0-1变量)
- One-Hot热编码(类似于哑变量)
在本案例中,将采用“字符转数值”的方法对离散型变量进行重编码
# 离散型变量的重编码
for feature in income.columns:
if income[feature].dtype == 'object':
income[feature] = pd.Categorical(income[feature]).codes
income.head(10)
| age | workclass | fnlwgt | education | education-num | marital-status | occupation | relationship | race | sex | capital-gain | capital-loss | hours-per-week | native-country | income | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 39 | 6 | 77516 | 9 | 13 | 4 | 0 | 1 | 4 | 1 | 2174 | 0 | 40 | 38 | 0 |
| 1 | 50 | 5 | 83311 | 9 | 13 | 2 | 3 | 0 | 4 | 1 | 0 | 0 | 13 | 38 | 0 |
| 2 | 38 | 3 | 215646 | 11 | 9 | 0 | 5 | 1 | 4 | 1 | 0 | 0 | 40 | 38 | 0 |
| 3 | 53 | 3 | 234721 | 1 | 7 | 2 | 5 | 0 | 2 | 1 | 0 | 0 | 40 | 38 | 0 |
| 4 | 28 | 3 | 338409 | 9 | 13 | 2 | 9 | 5 | 2 | 0 | 0 | 0 | 40 | 4 | 0 |
| 5 | 37 | 3 | 284582 | 12 | 14 | 2 | 3 | 5 | 4 | 0 | 0 | 0 | 40 | 38 | 0 |
| 6 | 49 | 3 | 160187 | 6 | 5 | 3 | 7 | 1 | 2 | 0 | 0 | 0 | 16 | 22 | 0 |
| 7 | 52 | 5 | 209642 | 11 | 9 | 2 | 3 | 0 | 4 | 1 | 0 | 0 | 45 | 38 | 1 |
| 8 | 31 | 3 | 45781 | 12 | 14 | 4 | 9 | 1 | 4 | 0 | 14084 | 0 | 50 | 38 | 1 |
| 9 | 42 | 3 | 159449 | 9 | 13 | 2 | 3 | 0 | 4 | 1 | 5178 | 0 | 40 | 38 | 1 |
对字符型离散变量的重编码效果,所有的字符型变量都变成了整数型变量,接下来就基于这个处理好的数据集对收入水平income进行预测。
在原本的居民收入数据集中,关于受教育程度的有两个变量,一个是education(教育水平),另一个是education-num(受教育时长),而且这两个变量的值都是一一对应的,只不过一个是字符型,另一个是对应的数值型,如果将这两个变量都包含在模型中的话,就会产生信息的冗余;fnlwgt变量代表的是一种序号,其对收入水平的高低并没有实际意义。故为了避免冗余信息和无意义变量对模型的影响,考虑将education变量和fnlwgt变量从数据集中删除。
income.drop(['education','fnlwgt'], axis=1, inplace=True)
income.head(10)
| age | workclass | education-num | marital-status | occupation | relationship | race | sex | capital-gain | capital-loss | hours-per-week | native-country | income | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 39 | 6 | 13 | 4 | 0 | 1 | 4 | 1 | 2174 | 0 | 40 | 38 | 0 |
| 1 | 50 | 5 | 13 | 2 | 3 | 0 | 4 | 1 | 0 | 0 | 13 | 38 | 0 |
| 2 | 38 | 3 | 9 | 0 | 5 | 1 | 4 | 1 | 0 | 0 | 40 | 38 | 0 |
| 3 | 53 | 3 | 7 | 2 | 5 | 0 | 2 | 1 | 0 | 0 | 40 | 38 | 0 |
| 4 | 28 | 3 | 13 | 2 | 9 | 5 | 2 | 0 | 0 | 0 | 40 | 4 | 0 |
| 5 | 37 | 3 | 14 | 2 | 3 | 5 | 4 | 0 | 0 | 0 | 40 | 38 | 0 |
| 6 | 49 | 3 | 5 | 3 | 7 | 1 | 2 | 0 | 0 | 0 | 16 | 22 | 0 |
| 7 | 52 | 5 | 9 | 2 | 3 | 0 | 4 | 1 | 0 | 0 | 45 | 38 | 1 |
| 8 | 31 | 3 | 14 | 4 | 9 | 1 | 4 | 0 | 14084 | 0 | 50 | 38 | 1 |
| 9 | 42 | 3 | 13 | 2 | 3 | 0 | 4 | 1 | 5178 | 0 | 40 | 38 | 1 |
上面表格呈现的就是经处理“干净”的数据集,所要预测的变量就是income,该变量是二元变量,对其预测的实质就是对年收入水平的分类(一个新样本进来,通过分类模型,可以将该样本分为哪一种收入水平)。
关于分类模型有很多种:
- Logistic模型
- **决策树 **
- K近邻
- 朴素贝叶斯模型
- 支持向量机
- 随机森林
- 梯度提升树GBDT模型等。
本案例将对比使用K近邻和GBDT两种分类器,因为通常情况下,都会选用多个模型作为备选,通过对比才能得知哪种模型可以更好地拟合数据。
4.2 拆分数据集
接下来就进一步说明如何针对分类问题,从零开始完成建模的步骤。基于上面的“干净”数据集,需要将其拆分为两个部分,一部分用于分类器模型的构建,另一部分用于分类器模型的评估,这样做的目的是避免分类器模型过拟合或欠拟合。如果模型在训练集上表现很好,而在测试集中表现很差,则说明分类器模型属于过拟合状态;如果模型在训练过程中都不能很好地拟合数据,那说明模型属于欠拟合状态。通常情况下,会把训练集和测试集的比例分配为75%和25%。
# 导入sklearn包中的函数
from sklearn.model_selection import train_test_split
# 拆分数据
X_train, X_test, y_train, y_test = train_test_split(income.loc[:,'age':'native-country'],
income['income'],train_size = 0.75,test_size=0.25, random_state = 1234)
# print(X_train)
# print(y_train)
print("训练数据集中共有 %d 条观测" %X_train.shape[0])
print("测试数据集中共有 %d 条测试" %X_test.shape[0])
训练数据集中共有 24420 条观测
测试数据集中共有 8141 条测试
上面的结果,运用随机抽样的方法,将数据集拆分为两部分,其中训练数据集包含24 420条样本,测试数据集包含8 141条样本,下面将运用拆分好的训练数据集开始构建K近邻和GBDT两种分类器。
4.3 搭建模型
# 导入K近邻模型的类
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import GradientBoostingClassifier
# 构件K近邻模型
kn = KNeighborsClassifier()
kn.fit(X_train,y_train)
print(kn)
#构件GBDT模型
gbdt = GradientBoostingClassifier()
gbdt.fit(X_train, y_train)
print(gbdt)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.1, loss='deviance', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
presort='auto', random_state=None, subsample=1.0, verbose=0,
warm_start=False)
首先,针对K近邻模型,这里直接调用sklearn子模块neighbors中的KNeighborsClassifier类,并且使用模型的默认参数,即让K近邻模型自动挑选最佳的搜寻近邻算法(algorithm=‘auto’)、使用欧氏距离公式计算样本间的距离(p=2)、指定未知分类样本的近邻个数为5(n_neighbors=5)而且所有近邻样本的权重都相等(weights=‘uniform’)。其次,针对GBDT模型,可以调用sklearn子模块ensemble中的GradientBoostingClassifier类,同样先尝试使用该模型的默认参数,即让模型的学习率(迭代步长)为0.1(learning_rate=0.1)、损失函数使用的是对数损失函数(loss=‘deviance’)、生成100棵基础决策树(n_estimators=100),并且每棵基础决策树的最大深度为3(max_depth=3),中间节点(非叶节点)的最小样本量为2(min_samples_split=2),叶节点的最小样本量为1(min_samples_leaf=1),每一棵树的训练都不会基于上一棵树的结果(warm_start=False)。
4.4 模型网格搜索法,探寻模型最佳参数
# K 近邻模型网格搜索法
# 导入网格搜索函数
from sklearn.grid_search import GridSearchCV
# 选择不同的参数
k_options = list(range(1,12))
parameters = {'n_neighbors':k_options}
# 搜索不同的K值
grid_kn = GridSearchCV(estimator= KNeighborsClassifier(), param_grid=parameters, cv=10, scoring='accuracy')
grid_kn.fit(X_train, y_train)
# 结果输出
grid_kn.grid_scores_, grid_kn.best_params_, grid_kn.best_score_
([mean: 0.81507, std: 0.00711, params: {'n_neighbors': 1},
mean: 0.83882, std: 0.00696, params: {'n_neighbors': 2},
mean: 0.83722, std: 0.00843, params: {'n_neighbors': 3},
mean: 0.84586, std: 0.01039, params: {'n_neighbors': 4},
mean: 0.84222, std: 0.00916, params: {'n_neighbors': 5},
mean: 0.84713, std: 0.00900, params: {'n_neighbors': 6},
mean: 0.84316, std: 0.00719, params: {'n_neighbors': 7},
mean: 0.84525, std: 0.00629, params: {'n_neighbors': 8},
mean: 0.84394, std: 0.00678, params: {'n_neighbors': 9},
mean: 0.84570, std: 0.00534, params: {'n_neighbors': 10},
mean: 0.84464, std: 0.00444, params: {'n_neighbors': 11}],
{'n_neighbors': 6},
0.8471334971334972)
GridSearchCV函数中的几个参数含义,estimator参数接受一个指定的模型,这里为K近邻模型的类;param_grid用来指定模型需要搜索的参数列表对象,这里是K近邻模型中n_neighbors参数的11种可能值;cv是指网格搜索需要经过10重交叉验证;scoring指定模型评估的度量值,这里选用的是模型预测的准确率。通过网格搜索的计算,得到三部分的结果,第一部分包含了11种K值下的平均准确率(因为做了10重交叉验证);第二部分选择出了最佳的K值,K值为6;第三部分是当K值为6时模型的最佳平均准确率,且准确率为84.78%。
# GBDT 模型的网格搜索法
# 选择不同的参数
from sklearn.grid_search import GridSearchCV
learning_rate_options = [0.01, 0.05, 0.1]
max_depth_options = [3,5,7,9]
n_estimators_options = [100, 300, 500]
parameters = {'learning_rate':learning_rate_options,
'max_depth':max_depth_options,
'n_estimators':n_estimators_options}
grid_gbdt = GridSearchCV(estimator= GradientBoostingClassifier(),param_grid=parameters,cv=10,scoring='accuracy')
grid_gbdt.fit(X_train, y_train)
# 结果输出
grid_gbdt.grid_scores_,grid_gbdt.best_params_, grid_gbdt.best_score_
([mean: 0.84267, std: 0.00727, params: {'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 100},
mean: 0.85360, std: 0.00837, params: {'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 300},
mean: 0.85930, std: 0.00746, params: {'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 500},
mean: 0.85213, std: 0.00821, params: {'learning_rate': 0.01, 'max_depth': 5, 'n_estimators': 100},
mean: 0.86327, std: 0.00751, params: {'learning_rate': 0.01, 'max_depth': 5, 'n_estimators': 300},
mean: 0.86929, std: 0.00767, params: {'learning_rate': 0.01, 'max_depth': 5, 'n_estimators': 500},
mean: 0.85459, std: 0.00767, params: {'learning_rate': 0.01, 'max_depth': 7, 'n_estimators': 100},
mean: 0.87076, std: 0.00920, params: {'learning_rate': 0.01, 'max_depth': 7, 'n_estimators': 300},
mean: 0.87342, std: 0.00983, params: {'learning_rate': 0.01, 'max_depth': 7, 'n_estimators': 500},
mean: 0.85438, std: 0.00801, params: {'learning_rate': 0.01, 'max_depth': 9, 'n_estimators': 100},
mean: 0.86855, std: 0.00907, params: {'learning_rate': 0.01, 'max_depth': 9, 'n_estimators': 300},
mean: 0.87248, std: 0.00974, params: {'learning_rate': 0.01, 'max_depth': 9, 'n_estimators': 500},
mean: 0.85962, std: 0.00778, params: {'learning_rate': 0.05, 'max_depth': 3, 'n_estimators': 100},
mean: 0.86974, std: 0.00689, params: {'learning_rate': 0.05, 'max_depth': 3, 'n_estimators': 300},
mean: 0.87326, std: 0.00697, params: {'learning_rate': 0.05, 'max_depth': 3, 'n_estimators': 500},
mean: 0.86978, std: 0.00790, params: {'learning_rate': 0.05, 'max_depth': 5, 'n_estimators': 100},
mean: 0.87543, std: 0.00897, params: {'learning_rate': 0.05, 'max_depth': 5, 'n_estimators': 300},
mean: 0.87445, std: 0.00962, params: {'learning_rate': 0.05, 'max_depth': 5, 'n_estimators': 500},
mean: 0.87338, std: 0.00927, params: {'learning_rate': 0.05, 'max_depth': 7, 'n_estimators': 100},
mean: 0.87391, std: 0.00964, params: {'learning_rate': 0.05, 'max_depth': 7, 'n_estimators': 300},
mean: 0.87072, std: 0.01012, params: {'learning_rate': 0.05, 'max_depth': 7, 'n_estimators': 500},
mean: 0.87211, std: 0.00989, params: {'learning_rate': 0.05, 'max_depth': 9, 'n_estimators': 100},
mean: 0.86851, std: 0.01048, params: {'learning_rate': 0.05, 'max_depth': 9, 'n_estimators': 300},
mean: 0.86229, std: 0.00857, params: {'learning_rate': 0.05, 'max_depth': 9, 'n_estimators': 500},
mean: 0.86626, std: 0.00660, params: {'learning_rate': 0.1, 'max_depth': 3, 'n_estimators': 100},
mean: 0.87355, std: 0.00802, params: {'learning_rate': 0.1, 'max_depth': 3, 'n_estimators': 300},
mean: 0.87449, std: 0.00842, params: {'learning_rate': 0.1, 'max_depth': 3, 'n_estimators': 500},
mean: 0.87383, std: 0.00878, params: {'learning_rate': 0.1, 'max_depth': 5, 'n_estimators': 100},
mean: 0.87310, std: 0.01001, params: {'learning_rate': 0.1, 'max_depth': 5, 'n_estimators': 300},
mean: 0.87236, std: 0.00939, params: {'learning_rate': 0.1, 'max_depth': 5, 'n_estimators': 500},
mean: 0.87502, std: 0.01037, params: {'learning_rate': 0.1, 'max_depth': 7, 'n_estimators': 100},
mean: 0.86953, std: 0.00873, params: {'learning_rate': 0.1, 'max_depth': 7, 'n_estimators': 300},
mean: 0.86192, std: 0.00823, params: {'learning_rate': 0.1, 'max_depth': 7, 'n_estimators': 500},
mean: 0.87154, std: 0.01075, params: {'learning_rate': 0.1, 'max_depth': 9, 'n_estimators': 100},
mean: 0.85995, std: 0.00848, params: {'learning_rate': 0.1, 'max_depth': 9, 'n_estimators': 300},
mean: 0.85328, std: 0.00828, params: {'learning_rate': 0.1, 'max_depth': 9, 'n_estimators': 500}],
{'learning_rate': 0.05, 'max_depth': 5, 'n_estimators': 300},
0.8754299754299755)
4.5 模型预测与评估
在模型构建好后,下一步做的就是使用得到的分类器对测试数据集进行预测,进而验证模型在样本外的表现能力。通常,验证模型好坏的方法有多种。
- 对于预测的连续变量来说,常用的衡量指标有均方误差(MSE)和均方根误差(RMSE);
- 对于预测的分类变量来说,常用的衡量指标有混淆矩阵中的准确率、ROC曲线下的面积AUC、K-S值等。
接下来,依次对上文中构建的四种模型(K近邻、K近邻网格搜索法、GDBT模型、GDBT网格搜索法模型)进行预测和评估。
4.5.1 K近邻模型在测试集上的预测
kn_pred = kn.predict(X_test)
print(pd.crosstab(kn_pred, y_test))
# 模型得分
print("模型在训练集上的准确率为%f" % kn.score(X_train, y_train))
print("模型在测试集上的准确率为%f" % kn.score(X_test, y_test))
income 0 1
row_0
0 5644 725
1 582 1190
模型在训练集上的准确率为0.889844
模型在测试集上的准确率为0.839455
第一部分是混淆矩阵,矩阵中的行是模型的预测值,矩阵中的列是测试集的实际值,主对角线就是模型预测正确的数量(income <=50K有 5644 人 和 income >50K 有 1190人),582和725就是模型预测错误的数量。经过计算,得到第二部分的结论,即模型在训练集中的准确率为88.9%,但在测试集上的错误率超过16%(1-0.839),说明默认参数下的KNN模型可能存在过拟合的风险。
模型的准确率就是基于混淆矩阵计算的,但是该方法存在一定的弊端,即如果数据本身存在一定的不平衡时(正负样本的比例差异较大),一定会导致准确率很高,但并不一定说明模型就是理想的。所以可以绘制ROC曲线,并计算曲线下的面积AUC值
from sklearn import metrics
# 计算ROC曲线的x轴 和 y轴数据
fpr, tpr, _ = metrics.roc_curve(y_test, kn.predict_proba(X_test)[:,1])
# 绘制ROC曲线
plt.plot(fpr, tpr, linestyle = 'solid', color ='red')
# 添加阴影
plt.stackplot(fpr, tpr, color='steelblue')
# 绘制参考线
plt.plot([0,1],[0,1],linestyle='dashed', color='black')
# 添加文本
plt.text(0.6, 0.4, 'AUC=%.3f' % metrics.auc(fpr,tpr), fontdict=dict(size =16))
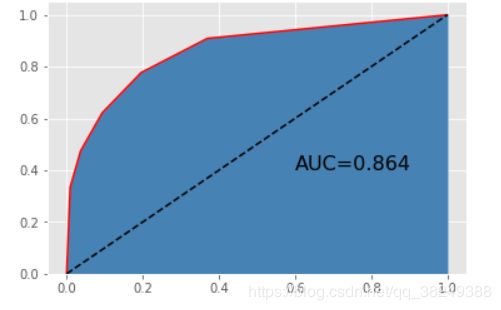
plt.show()
上图绘制了模型的ROC曲线,经计算得知,该曲线下的面积AUC为0.864。使用AUC来评估模型的好坏,那应该希望AUC越大越好。一般而言,当AUC的值超过0.8时,基本上就可以认为模型比较合理。所以,基于默认参数的K近邻模型在居民收入数据集上的表现还算理想。
4.5.2 K近邻网格搜索模型在测试集上的预测
from sklearn import metrics
grid_kn_pred = grid_kn.predict(X_test)
print(pd.crosstab(grid_kn_pred, y_test))
# 模型得分
print("模型在训练集上的准确率为%f" % grid_kn.score(X_train, y_train))
print("模型在测试集上的准确率为%f" % grid_kn.score(X_test, y_test))
fpr, tpr, _ = metrics.roc_curve(y_test, grid_kn.predict_proba(X_test)[:,1])
plt.plot(fpr, tpr, linestyle = 'solid', color ='red')
plt.stackplot(fpr, tpr, color='steelblue')
plt.plot([0,1],[0,1],linestyle='dashed', color='black')
plt.text(0.6, 0.4, 'AUC=%.3f' % metrics.auc(fpr,tpr), fontdict=dict(size =16))
plt.show()
income 0 1
row_0
0 5838 861
1 388 1054
模型在训练集上的准确率为0.882924
模型在测试集上的准确率为0.846579
相比于默认参数的K近邻模型来说,经过网格搜索后的模型在训练数据集上的准确率下降了,但在测试数据集上的准确率提高了,这也是我们所期望的,说明优化后的模型在预测效果上更加优秀,并且两者差异的缩小也能够降低模型过拟合的可能。再来看看ROC曲线下的面积,网格搜索后的K近邻模型所对应的AUC为0.87,相比于原先的KNN模型提高了一点。所以,从模型的稳定性来看,网格搜索后的K近邻模型比原始的K近邻模型更加优秀。
4.5.3 GBDT模型在测试集上的预测
from sklearn import metrics
gbdt_pred = gdbt.predict(X_test)
print(pd.crosstab(gbdt_pred, y_test))
# 模型得分
print("模型在训练集上的准确率为%f" % gbdt.score(X_train, y_train))
print("模型在测试集上的准确率为%f" % gbdt.score(X_test, y_test))
fpr, tpr, _ = metrics.roc_curve(y_test, gbdt.predict_proba(X_test)[:,1])
plt.plot(fpr, tpr, linestyle = 'solid', color ='red')
plt.stackplot(fpr, tpr, color='steelblue')
plt.plot([0,1],[0,1],linestyle='dashed', color='black')
plt.text(0.6, 0.4, 'AUC=%.3f' % metrics.auc(fpr,tpr), fontdict=dict(size =16))
plt.show()
income 0 1
row_0
0 5869 780
1 357 1135
模型在训练集上的准确率为0.869861
模型在测试集上的准确率为0.860337
集成算法GBDT在测试集上的表现明显要比K近邻算法优秀,这就是基于多棵决策树进行投票的优点。该模型在训练集和测试集上的表现都非常好,准确率均超过85%,而且AUC值也是前面两种模型中最高的,达到了0.914。
4.5.4 网格搜索的GBDT模型在测试集上的预测
from sklearn import metrics
grid_gbdt_pred = grid_gbdt.predict(X_test)
print(pd.crosstab(grid_gbdt_pred , y_test))
# 模型得分
print("模型在训练集上的准确率为%f" % grid_gbdt.score(X_train, y_train))
print("模型在测试集上的准确率为%f" % grid_gbdt.score(X_test, y_test))
fpr, tpr, _ = metrics.roc_curve(y_test, grid_gbdt.predict_proba(X_test)[:,1])
plt.plot(fpr, tpr, linestyle = 'solid', color ='red')
plt.stackplot(fpr, tpr, color='steelblue')
plt.plot([0,1],[0,1],linestyle='dashed', color='black')
plt.text(0.6, 0.4, 'AUC=%.3f' % metrics.auc(fpr,tpr), fontdict=dict(size =16))
plt.show()
income 0 1
row_0
0 5835 669
1 391 1246
模型在训练集上的准确率为0.889271
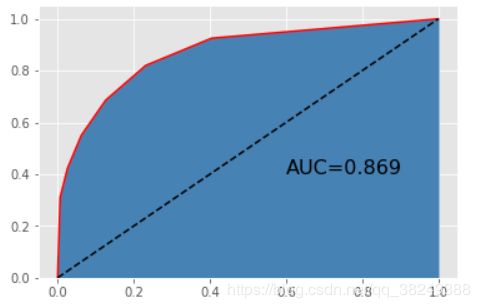
模型在测试集上的准确率为0.869795
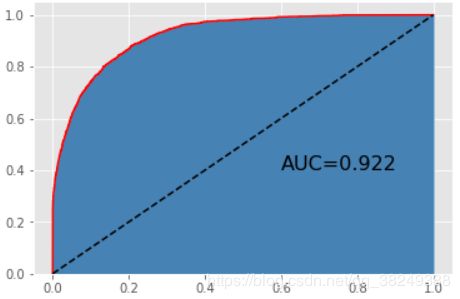
基于网格搜索后的GBDT模型的表现,从准确率来看,是4个模型中表现最佳的,该模型在训练集上的准确率接近89%,同时,在测试集上的准确率也超过86%;从绘制的ROC曲线来看,AUC的值也是最高的,超过0.92。
不论是K近邻模型,还是梯度提升树GBDT模型,都可以通过网格搜索法找到各自的最佳模型参数,而且这些最佳参数的组合一般都会使模型比较优秀和健壮。所以,纵向比较默认参数的模型和网格搜索后的最佳参数模型,后者可能是比较好的选择(尽管后者可能会花费更多的运行时间);横向比较单一模型和集成模型,集成模型一般会比单一模型表现优秀。
5.实验总结
本次收入预测问题属于机器学习中的聚类问题,主要是通过数据集中的income变量将数据分成了两个类别(年收入大于5W和年收入小于等于5W)。
本次实验主要收获是:
- 1.熟悉了数据挖掘的重要流程(预览数据集,明确分析的目的–导入数据并数据预处理–探索数据特征–清洗数据,构建模型–模型预测,模型评估)。
- 2.初步了解了python sklearn中的两个机器学习模型K近邻和GBDT(梯度提升树)和用网格搜索法改进模型参数优化模型。
- 3.本章还学习到了pands,matplotlib。